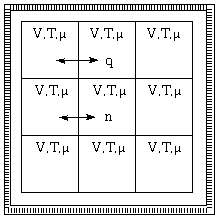
The grand canonical ensemble - V, T fixed, heat permiable and particles also permiable

Our constraints are:
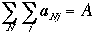 |
Total occupation |
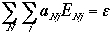 |
Total energy |
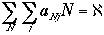 |
Total number of particles |
The number of states is given by multinomial coeff.
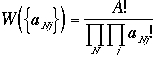
As we have done before, the most probable configuration is obtained by
its maximum of W subject to constraints above, and obtained
by using Lagrange multiplier method,
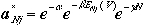
Then, the probability of finding particles in states given by N and
j is
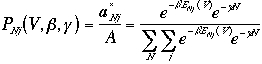
The term in the denominator is the grand canonical partition
function.
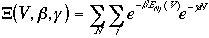
As we have seen before, the average mechanical properties are calculated by
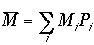
Then, the averages of the E, P, and N are
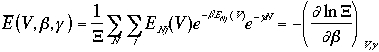
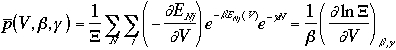
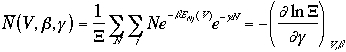
A grand canonical ensemble can be considered as a collection of canonical ensembles in thermal equilibrium each other and with all possible values of N.
Imagine that at one instance the wall becomes inpermeable, but still conducting heat. Then, the ensemble becomes a collection of canonical ensemble with N, V, and T fixed. We know from before that b = 1/kT.
g is obtained by the same method, i. e. to make a function f that depends on b, g and {EN,j(V)}, and to show b to be an integrating factor for dqrev.
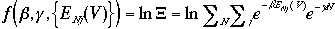
The total derivative of f is
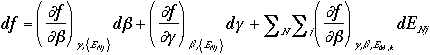
and we can arrive at
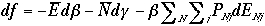
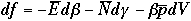
Changing notation,
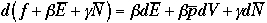
Now, compare this with the macroscopic thermodynamic eqation
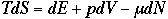
Using b = 1/kT,
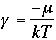
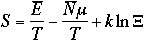 1)
1)
Therefore, the grand canonical partition function is given as
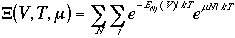
|
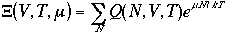
One can write chemical potential as
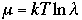
where l
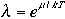
l is called an absolute activity
If we compare Eq. 1) with a thermodynamic function G
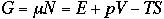
we see that
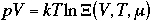
The summary of thermodynamic equations derived can be found on a
table.
Fluctuations
Fluctuations in Energy
We know that the second central moment, called variance, is a measure of
spread of a probability distribution about the mean value. Consider
first fluctuations in energy for a canonical ensemble. Variance in energy
is given by
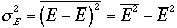
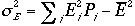 2)
2)
Since
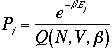
The first term on the right-hand side of Eq. 2) is
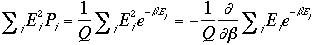
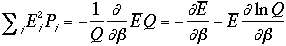
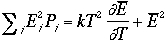
Therefore, the variance
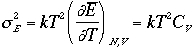
The relative magnitude of the spread is given by
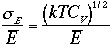
Then, by using ideal gas the values of average E and
s, the order of magnitude for the
respective variables are O(NkT) and O(Nk). Therefore,
the ratio is O(N-1/2), and for an ensemble approximating
a macroscopic quantity, the relative deviation is very small!
Fluctuations in Number of Particles
Now let's calculate the variance in the number of particles, N,
while V, T, and m are fixed.
As we have done before,
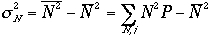 3)
3)
Since
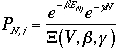
The frist term of the right hand side of Eq. 3) is
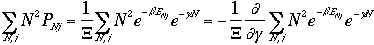
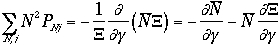
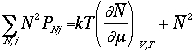
We arrive at
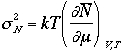
From the thermodynamics,
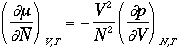
Therefore, we have
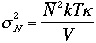
where k is isothermal compressibility
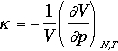
The relative magnitude of sN
to the average N
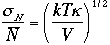
We can estimate the ratio using ideal gas, as described above.
We can use k = 1/p, then the ratio
is
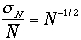
Therefore, our estimation of the order of magnitude for a macrosopic
quantity is very small. The width is very very narrow!
All ensembles considered, ...
In a canonical ensemble, we can write a partition function
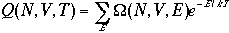
As we have seen that the deviation from the mean is extremely small, and
in the limit of very large number of particles, N, we only have to
consider one value of E, i.e.
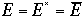
Then, the canonical partition function becomes
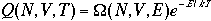 4)
4)
It means that the canonical ensemble can be represented as a microcanonical
ensemble. Effectively the average energy is the only energy that
each system can possess, even though in principle all energy levels are
available to systems in the ensemble.
If we take the natural function of lnQ, which is Helmholtz free energy (A = E - TS), and substitute Eq. 4), then
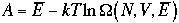 5)
5)
Thus,
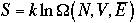
Therefore, the second term in the right-hand side of Eq. 5) is
entropy. This is an alternative derivation of entropy.
Similarly, a grand canonical ensemble can take any value of N and E, the total number of particles and the total energy of the ensemble is practically constant!
All ensembles we discussed are equivalent! It is matter of convinience in the choice of ensemble one uses.