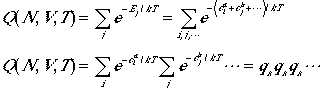Boltzmann, Fermi-Dirac, and Bose-Einstein Statistics

The form of the partition functions will be shown to be different depending on whether the particles are distinguishable or not. Furthermore, if the particles are boson or fermion, the form of the partition functions also differ. As a consequence, the distribution of particles will also differ. These are the topics we will discuss in this lecture.

Distinguishable Particles

We have discussed that a completely coupled (all degrees of freedom are mixed in the Hamiltonian) Schrodinger equation is not tractable for any practical purpose. We have introduced a separable approximation of the wavefunctions in several degrees of freedom. We have written wavefunctions in a product form, therefore, the total energy of the system is a trace. Then, we can write canonical partition function in the following form: 
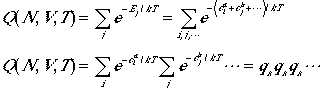                                   (1)
We can do this:
if Hamiltonian can be written as a sum of independent terms
if particles are distinguishable!

If the energy of all particles are the same, the above equation becomes
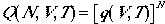for Distinguishable Particles (2)
where q(V,T) is called a molecular partition function.

As we have seen in the discussion above, the Hamiltonian can be separated into a sum of various degrees of freedom, and therefore, we can write 

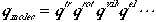                                (3)

Tremendous simplification in calculating partition functions is achieve by using Eqns. (1) and (3); we have reduced an N-body problem to one-body problem, and further reduced to individual degrees of freedom of one particle.

Indistinguishable Particles


What happens if the particles not distinguishable, which is likely the case for molecules in general.

The total energy of the system and the partition function are 

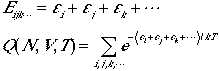                                (4)
Since the particles are indistinguishable, we can not do what we did in Eqn. (1), i.e. to sum the indices individually.

Consider the following, where all indices except one is the same, 

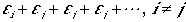                                (5)
Since the indices are just dummy the position of ei is not important. If we sum over all states, we overcount the sum by N.

Consider another case, where all indeces are different, such that 

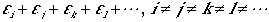                                (6)
The N! states obtained by permuting N different subscripts are identical, and occur only once in the summation. But, in general, it occurs N! times.

Reality lies somewhere between the two extreme above. However, if we consider that there are many many more states available to the particles, then we have the latter situation.

The number of quantum states available to the system for energy less than e is of order O(1030), if we use a particle-in-a-box (3D) approximation; mass = 10-22g in a 10 cm cube at 300 K. This shows that the available quantum states are much larger than the number of the particles in the system! Hence, molecules can choose quantum states of choice, and the summation in Eqn. (4) should have different indices occupied.

Then, by summing over all states and then divide by N!, and we arrive at.

Approximation to Eqn. (4) for indistinguishable particles
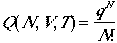for # of available quantum states >> N (7)
where
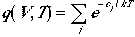
Indistinguishability of the particles is incorporated into the equation with the condition that the number of available quantum states to be much larger than the number of particles. This is said to obey Boltzmann statistics. The condition for Boltzmann statistics is to have large mass, high temperature and low density. Such condition is the classical mechanics limit.

The total energy of the N-body system is
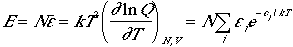
Therefore, the average energy of a particle is 
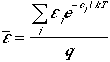                      (8)
which leads to the probability that a molecule is in the jth state is 
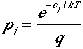                      (9)
It follows that the fluctuations in molecular energies can be shown
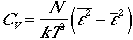
and the fluctuations in energies are of order e. A sharp probability distribution seen in previous sections are many-body effect!

Fermi-Dirac and Bose-Einstein Statistics

Consider a grand canonical ensemble. Let Ej(N,V) be the available states for N molecule system, and ek be the molecular quantum states. The energy of the system is given by
and also
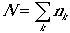
Canonical partition function, Q(N,V,T) can be written as 
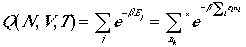                                (10)
The asterisk in the summation denotes for the restriction that the total number being fixed at N.

It turns out that this restriction is mathematically awkward in canonical ensemble. By using a grand canonical ensemble, the evaluation of the partition functions are easier. We write the grand canonical partition function as 

           .
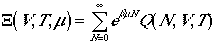This can be written as
by defining l = ebm. Then, we arrive at
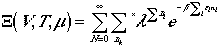
Since we are summing over all values of N, each nk ranges over all possible values, we can write
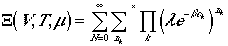
It can, then, be rewritten as
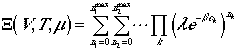
and arrive at a general expression
(11)

Now for a fermion system, the occupation, nk can only be 0 or 1 due to Pauli exclusion principle. Therefore, n1max = 1, and arrive at:
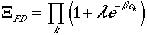Fermi-Dirac Statistics (12)

For a boson system, there is no restriction in occupation therefore, nk extends to infinity, and we have
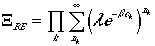
However, if we use the following math. identity,
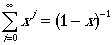
we can arrive at:
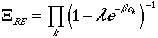Bose-Einstein Statistics (13)
The difference between Fermi-Dirac and Bose-Einstein statistics is in the sign inside of the parenthesis and the sign of the exponent.

Since average N can be written as,
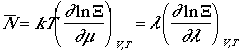
It follows that
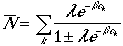
Therefore, the average number of particles in the kth quantum state is given by
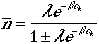
which is in analogy with Eqn. (9) above. Then the average energy in quantum statistics is given by
We can also derive expression for the following.

Next, we will look at ideal monatomic and diatomic gases.