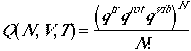 (1)
(1)
Ideal gas: dilute, noninteracting monatomic species that can be represented well by pV = NkT (or pV = nRT), under 1 atm. and T > ambient temperature.
Again we are dealing with indistinguishable particles, we can use the same results as we had in the previous lecture. We have
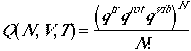 (1)
(1)
The traslational partition function is similar to monatomic case,
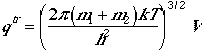 .
.
Rigid Rotor-Harmonic Oscillator Approximation
Diatomic molecules have rotational as well as vibrational degrees
of freedom. If we approximate rotation and vibration to be separable,
i.e.
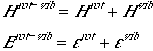 .
.
The partition function can, then, be written as Eqn. (1). Here we also have
used Born-Oppenheimer approximation to separate out the vibration and
electronic degrees of freedom.
Rigid Rotor Approximation
The separable approximation used for rotation is called rigid rotor
approximation, where rotation does not affect changes might occur in
the body. The change might be of elongation due to centrifugal force.
Quantum mechanically, the rotational eigenvalues and their degeneracy are
given by
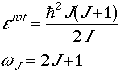 (2)
(2)
where I is the moment of inertia,
mre2, of the diatomic
molecule and J is the rotational quantum numbers
(J = 0, 1, 2, ...). Eqn. (2) can be written in terms of
rotational constant, B
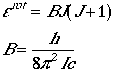 .
.
Therefore, we can write rotational partition function as
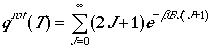
High Temperature Limit
We can use similar summation --> integration transformation can be done
if the energy levels are close to each other. If we define
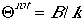
which is called the characteristic temperature of roation.
If the term, Qrot/T, is small
enough we can approximate the summation by an integral. Therefore, we
have
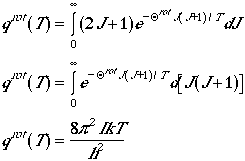
for Qrot << T.
Low Temperature Limit
The low temperature
limit may be calculated explicitly including the summation, such that
for HD molecule
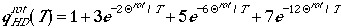
which give us a good approximation as long as Q
rot > 0.7T.
Intermediate Temperature
For intermediate region, we need other
approximation.
We use Euler-MacLaurin summation formula to approximate a function. The Euler-MacLaurin formula is often used in a numerical integration of a function.
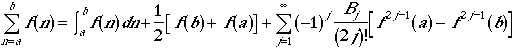
where Bj is the Bernoulli numbers (B1 =
1/6, B2 = 1/30, B3 = 1/42,...
For rotational partition function, one obtains
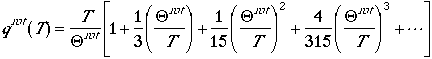
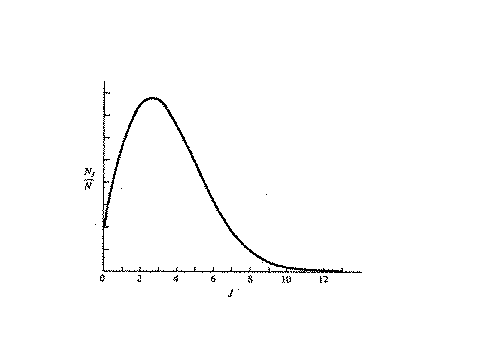
It is interesting to note that the distribution of the rotation at
certain temperature has a maximum. If we write the fraction of molecules
in jth rotational state
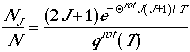
and differentiate the fraction with respect to J, we can arrive at
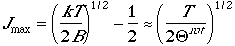
Case in point, the following figure shows the rotational population
as a function of J.
We first expand potential energy (interaction between atoms) function V(r) at equilibrium geometry in a Taylor series.
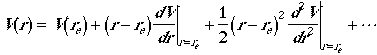
Since evaluation is done at the equilibrium geometry, the second term
on the right-hand side is zero and the first term is chosen to be
zero, and truncating the expansion at the second order. Then, the
V(r) can be written as
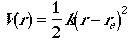
where k is a force constatnt. This is called Harmonic approximation.
When the potential, V(r), is used for vibrational Schrodinger
equation, then one obtains
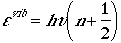 for n = 0, 1, 2, ...
for n = 0, 1, 2, ...
where u is the frequency and n is
a vibrational quantum number. The degeneracy is always one in the case
of diatomic molecules. Note also that n starts at zero!
The frequency is written as
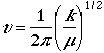
and m is a reduced mass,
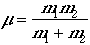 .
.
Using the above expressions the vibrational partition function is written as
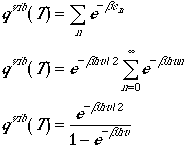 , (3)
, (3)
and we have used a series expansion in a geometric series.
Contrary to the rotational partition function we have a closed expression
for the partition function. In arriving at Eqn. (3), we have used
no approximation (other than harmonic approximation).
The fraction of molecules in the vibrational state n can be obtained by
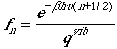 .
.
The fraction of molecules that in the excited states is
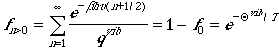 .
.
The fraction is exponentially decaying function! Therefore, the ground
state is the only state that are populated in vibrations.
Electronic Partition Function
If we take the zero of energy in the electronic state to be the dissociated
atom limit, we can write the partition function for electronic part as
We can write
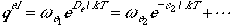 .
.
Generally, only the ground state is populated, and therefore, we can
truncate the equation to have only the first term. Here, De
denotes the dissociation energy of the diatomic molecule (not to be
confused with the D0).
Thermodynamic Functions
The total molecular partition function found in Eqn. (1) can now
be written as
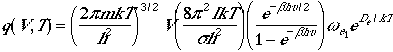 . (4)
. (4)
We have used rigid-rotor harmonic oscillator approximation to derive
Eqn. (4). In deriving, we have restrictions that
Qrot << T and only the ground electronic
state is populated.
Using Eqn. (4), we can arrive at the following thermodynamic functions;
| Energy | 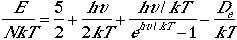 |
| Heat capacity | 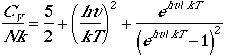 |
| Entropy | 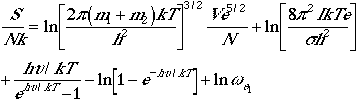 |
| Pressure | 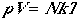 |
| Chemical potential | 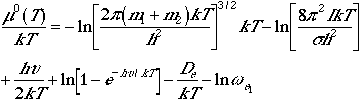 |