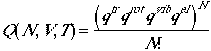 . (1)
. (1)
We have already seen most of the important development for partition functions of poly atomic molecules in monatomic and diatomic gases. There are only minor differences in the partition functions.
We will treat rotations in the classical limit for polyatomic molecules. We will also need to develop hindered rotations in nearly free-rotor vibrations, such as methyl group rotations. As we did in the monatomic and diatomic gases, we can write a canoincal partition function as
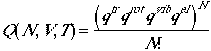 . (1)
. (1)
The traslational partition function is similar to monatomic case,
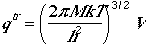
where M is the molar mass of the polyatomic molecule.
The electronic partition function is, as before, expressed as
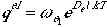 .
.
Here we assume that only the ground electronic state contributes,
and notice the zero of the energy is given at the bottom of the well and
De is the dissociation energy.
As we have seen in diatomic gas, we will utilize the Taylor series expansion of potential energy truncated at the second-order as our basis for vibrational motion. We have 3N - 6 degrees of vibrational freedom (3N - 5 for a linear molecule) in polyatomic molecules. If we approximate the vibrational wavefunctions to be as the product form, then we can separate each degree of freedom, hence the partition function is also a product of each degree of freedom. The procedure for obtaining the vibration wavefunction is called normal mode analysis.
Normal Mode Analysis
The potential energy is given by, as before
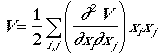 .
.
We can write the the coordinates in terms of mass-weighted cartesians
 .
.
Then the Schrodinger equation is and the energy is the sum of the
3N - 6 degrees of freedom.
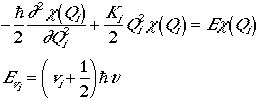 .
.
The partition function for polyatomic vibration is written in the
form
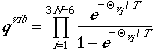 ,
,
where TVj is the characteristic
temperature of the jth normal mode.
Linear Molecules
The rotational energy and degeneracy of a linear molecule is given by

where J = 0, 1, 2,...m and I is the moment of inertia
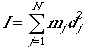
where dj is the jth distance
from the center of mass, which is given by
 .
.
The rotational partition function is then
 .
.
Non-linear Molecules
The rotational energies of the non-linear rigid body depends on
the symmetry in terms of the rotational constants of the molecule.
We define moments of inertia
 .
.
As it is seen above, there exists cross terms. We can get rid of
the cross terms by aligning the molecule on the principal axis.
Therefore, in general, we have three rotational constants,
 .
.
If IA = IB = IC, the rigid
body is called a sphereical top;
if IA = IB, but not IC
then it is called a symmetric top;
and if all are different, it is called an asymmetric top.
Spherical Top
The energy levels and degeneracy is given by
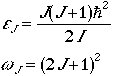 .
.
The partition function in the high temperature limit is given by
 .
.
By neglecting 1 in the parenthesis, since at high temperature
J is much larger than 1, then
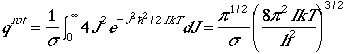 .
.
Symmetric Top
The energy levels and degeneracy of a symmetric top is given by
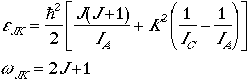 ,
,
where K = J, J-1, J-2, ... , -J.
The partition function is given by
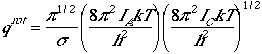 ,
,
Asymmetric Top
Since quantum mechanical problem of the asymmetric top rotation
is quite cumbersome, and we utilize classical mechanics to derive
the following after lengthy and complecated algebra.
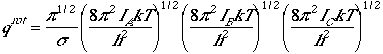 .
.
| Nonlinear Polyatomic Molecules | |
|---|---|
| Partition Function | 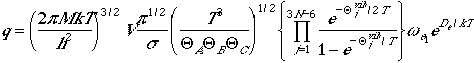 |
| Helmholtz Energy |  |
| Internal Energy |  |
| Heat Capapcity | 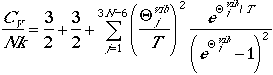 |
| Entropy |  |
| Pressure | 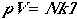 |
When nearly free rotation of a group is present in a molecule, the molecular partition function has to be modified. An example of such is the rotation of methyl group in ethane, as seen below.
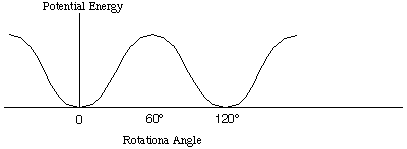
The torsional motion of the methyl groups in ethane stays close to the
bottom of the potential energy, and the vibrational motion is well
represented by the harmonic motion (normal mode). However, at higher
temperature, the torsional motion becomes nearly free rotation.
Therefore, we must make correction for this motion.
The potential energy function for the hindered rotation is given by
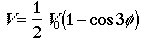 .
.
In order to solve for e the Schrodinger
equation,
 ,
,
must be solved. Here Ihr is an effective moment of inertia.