Chapter 2. Atomic Structure and Motivations

Failure of Classical Physics

Toward the end of 19^th century, physics was highly successful. Thought to be nearly completed in understanding the physical world, and the future generation was to push the limits of accuracy to larger decimal places.

.... except some minor details.

1. Black-body radiation
2. Heat capacity
3. Atomic and molecular spectra
4. Photoelectric effect
5. Is light wave or particle?

These allegedly minor details were to transform the view of our world completely different, leading to quantum mechanics. Let us look at these in more details.

Black-Body Radiation

Discovery of Electron

As we know, gas is generally an insulator. However, with high electrical tension, gas becomes conducting. A good example is lightening storm.

Conduction of gas with high electrical tension can be produced in a laboratory environment using Crooks tube. It contains low-pressure noble gas in a closed glass tube containing two conducting plates at two ends, which are connected to a battery to create high voltage across the plates.

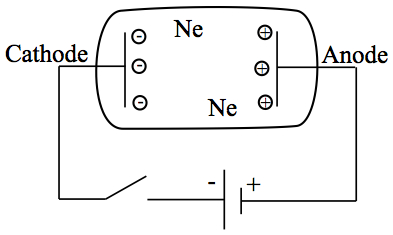
Figure 1. Crooks tube.

A neon sign is made using this principle.

Jean Perrin (France) inserted a metal plate to Crooks tube, and observed that the inserted plate acquired negative charge. In 1897, J J Thomson modified Crooks tube further, as shown in Figure 2.

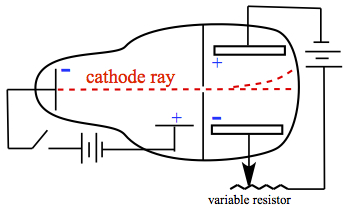
Figure 2. Thomson's cathode ray tube.

Thomson's idea was to subject the cathode ray with electric field and magnetic field to see the response. If cathode ray was charged, one would observe deflection by electric and magnetic fields. In the electric field, the cathode ray was deflected toward the positive side of the plate. In the case of effect of magnetic field, Thomson placed a magnet as shown in Figre 3.

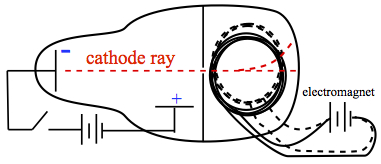
Figure 3. Thomson's cathode ray tube with magnet.

Lorentz cleaned up the mathematics that was originally provided by Thomson, and the force incurred on the cathode ray is now given by Lorentz force,

F = q (E + v_{0} B)

The first term on the right-hand side is the effect of electric field, and the latter for magnetic field effect, with v₀ is the velocity of the cathode ray.

Cathode Ray in Electric Field

Let us look at electric field effect first. Starting with the Newton's law of motion, F_e = ma. F_e indicates the force due to electric field.

a_{y} = \frac{F_{e}}{m} = \frac{q E}{m} = - \frac{e E}{m}

where a_y is the accerelation in the deflection direction, y. Also, q = -e for electron.

If the deflection y is expanded in Taylor series at y₀ in t, but truncated at the second order in t, one gets

y = y_{0} + v_{0} t + \frac{1}{2} a t^{2}

where v₀ and a are,

$v_{0} = \frac{d y}{d t}$	5
$a = \frac{d^{2} y}{d t^{2}}$	6

The deflection is initially zero, thus y₀ = 0 and v₀ = 0. So, the expansion is

y = \frac{1}{2} a t^{2}

Since the accerelation is given in Eqn. 3, we have

y = - \frac{e E t^{2}}{2 m}

If we assume the motion in the x direction to be constant motion, then x = v_xt and a = 0. Thus,

t = \frac{x}{v_{x}}

Substituting Eqn. 9 into Eqn. 8, one gets,

y = - \frac{e E x^{2}}{2 m v_{x}^{2}}

Therefore, the deflection is proportional to

y \propto \frac{e E}{m v_{x}}

Cathode Ray in Magnetic field

Now, we examine the second term in Eqn. 2. We follow the analogous arguments above. The Newton's law of motion in magnetic field is F_b = ma.

F_{b} = - e v_{0} B = m a_{y}

We now relate a to another kinematic equation,

v^{2} = v_{0}^{2} + 2 a (x - x_{0})

By solving for a in Eqn. 13, and substitute into Eqn. 12, one obtains

y = - \frac{e B x^{2}}{2 m v_{x}}

The deflection observed in the magnetic field is proportional to

y \propto \frac{e B}{m v_{x}}

Charge to Mass Ratio

In both cases, deflection by electric field and magnetic field, the quantity e/m can be deduced from the experiment. J.J. Thomson in 1897 calculated the e/m or charge to mass ratio. The value of e/m today is 1.76 x 10¹¹ C/kg. The observation are consistent with the cathode ray has negative charge, and today we call it, electron.

+ Mass Spectrometry

One of the most versatile instruments in chemical laboratory is mass spectrometer. The fundamentals of mass spectroscopy is the given by the deflections observed in Eqns. 10 and 14.

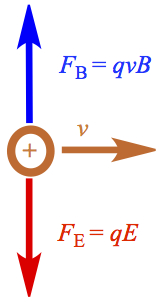
When a charged, say positive, particle comes in from left after passing through the slit 1, S₁, the charged particle feel a force of electric and magnetic field that are lined up according to Figure C1.


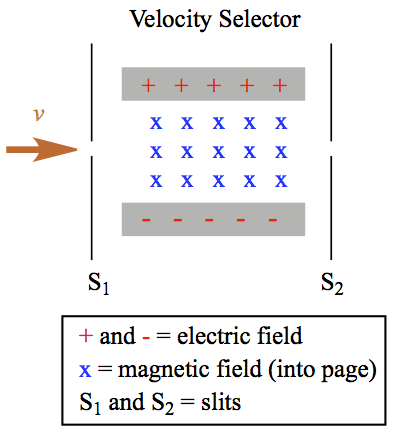Figure C1. Velocity selector of charged particle.	Figure C2. Charged particle in electric and magnetic fields.

If only the electric field is turned on, the positively charged particle would feel downward force. If on the other hand, only magnetic field is turned on, upward force would be felt by the particle. In this case the magnetic field is pointing toward the rear of the computer display you're looking at. If and when the electric and magnetic forces are equal,

F_{E} + F_{B} = 0

The situation is shown in Figure C2. It means that the charged particle would proceed to the opening in S₂ that is lined up with the opening of S₁. Then, the following relationship must be true.

q E = q v B

v = \frac{E}{B}

It shows that the velocity of the charged particle can be selected by adjusting the electric field and magnetic field.

Mass spectrometer is illustrated in Figure C3.

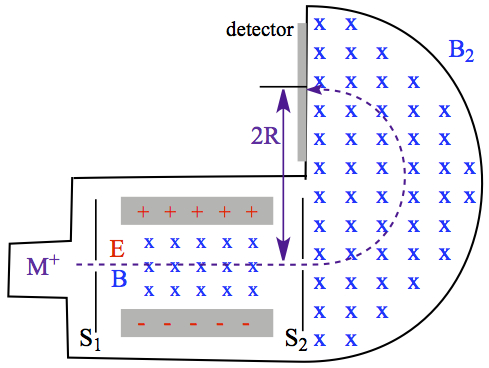
Figure C3. Mass spectrometer.

Molecules injected are ionized generally by electrical discharge, and creating ion, M⁺. The ion enters into the velocity selector, described above, and after velocity selection the ion enters into a semiciruclar chamber with magnetic field, B₂. The ion follows the semicircular path (dashed line) to reach the detector. The observed point is separated to the exiting slit S₂ of the velocity selector by a diameter of the semicircle path, labeled 2R, twice the radius.

The magnetic force acting on the ion is F = qvB₂. When a mass, m, is in constant circular motion (or constant velocity), it would feel the centripetal acceleration, a_C,

a_{C} = \frac{v^{2}}{R}

where R is the radius of the circular motion. On the semicircular path, the magnetic force and the centripetal force are equal.

q v B_{2} = \frac{m v^{2}}{R}

Therefore, the mass can be calculated as

m = \frac{q B B_{2} R}{E}

In Eqn. C6, E and B are the electric and magnetic fields of mass selector, and B₂ is of the semicircular chamber.

Millikan's Oil Drop Experiment

In order to determine the value of the fundamental unit of charge e, Millikan set out to measure it by through the so-called oil drop experiment. The device is set up as follows, in Figure 4.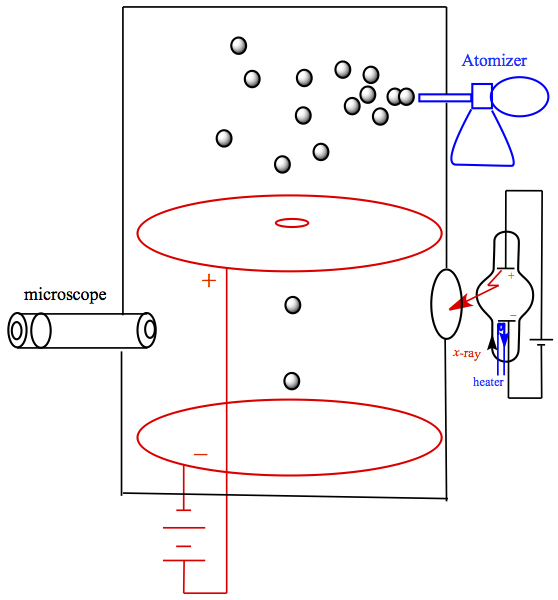

Figure 4. Millikan's Oil Drop Experiment

The temperature controlled box equipped with atomizer containing oil and microscope. When atomizer generates a spray of tiny oil droplets, some of the droplets would fall in a hole on a metal plate that is connected with an electrical source. When these droplets fall due to gravity, one can calculate the radius of droplets by considering drag (Stokes' law) generated by air resistance to fall. The terminal velocity, v_f of droplets can be measured by looking into the microscope on the device. The situation is shown in Figure 5a.

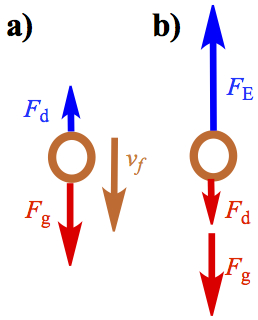
Figure 5. Forces Associated with Oil Drop Experiment. a) Electric field off. b) Electric field on.

The drag force is given by

F_{d} = 6 π r η v_{t}

where r is the radius of droplet, η is viscosity of air, and v_t is the terminal velocity of droplet. The force of gravity is, as you know, F_g = mg. However, one must take into account of apparent mass (weight) by using densities of air and the droplet, then the force is,

F_{g} = \frac{4}{3} π r^{3} (ρ - ρ_{a i r}) g

The force acting on the droplet with its terminal velocity v_f is to equate F_d = F_g, and rearranging it to yield the radius of the droplet,

r = 3 {(\frac{η v_{t}}{2 (ρ - ρ_{a i r}) g})}^{1 / 2}

from which one otains the mass of the droplet to be,

m = \frac{4}{3} π r^{3} ρ

Now that we have a way to measure radius and mass of droplets, we need to charge it by ionizing the molecules of air by X-ray. The ionized air molecules adheres to the surface of the oil droplets. When electric field is turned on, and adjust the electric field by changing the voltage across the two plates, such a way that the droplet stops downward motion. Then, the electrical force, F_E, becomes equal to the downward force of gravity, F_g, and the drag force, F_d. The drag force is now applied to go against the upward motion of droplet.

F_{E} = F_{g} + F_{d}

The situation is described in Figure 5b. The electric field is given by E = V/d where V is the voltage across the two plates, and d is the distance between the plates. Then, the charge q on the droplet can be calculate using Eqn. 20, as

q = \frac{d}{V} [6 π r η v_{t} + \frac{4}{3} π r^{3} (ρ - ρ_{a i r}) g]

What Millikan found was that the charge, q, on droplets consist of multiples of small charge unit, q = n e. After many experiments, he obtained the value of e to be 1.592 x 10^-19 C (today's value is 1.60219 x 10^-19 C).

From the result of e and using the e/m ratio of 1.76 x 10¹¹ C/kg, we can arrive at the mass of electron. The mass of electron is calculated to be 9.10 x 10^-31 kg.

Light

We saw in Chapter 1 that light is electromagnetic wave. History of light being a wave is quite long.

Diffraction of light through single-slit

When the monochromatic light goes through a slit and observed at a distant detector, you might see the intensity of light is as shown below in Figure 5. Note that there are diffraction fringes seen in the figure.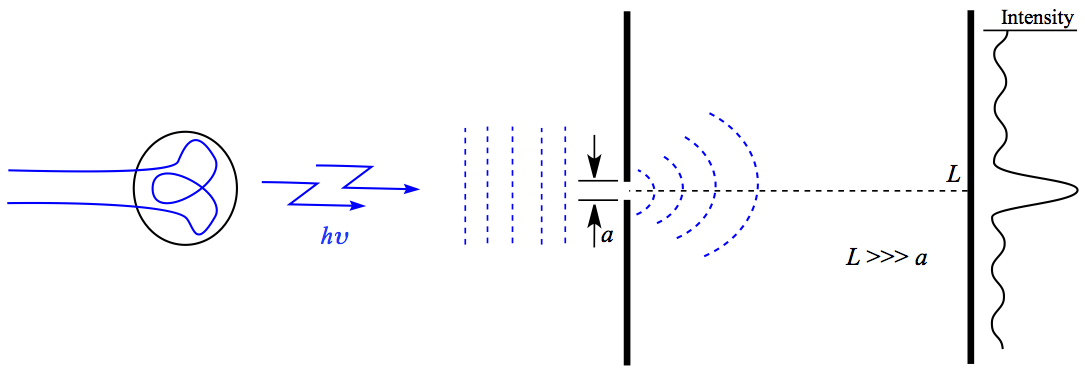

Figure 5. Light through Single-slit.

When the monochromatic light from a source at a distance passing through a narrow slit of dimension a, we can think about a scenario that the light comes in an angle, as shown in Figure 6.

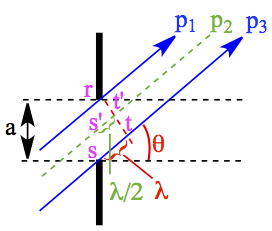
Figure 6. Configuration of Single-slit Experiment.

In comparison to the top beam path, p₁, and the bottom one p₃, the light has to travel a full wave length, λ, more distance to reach the monitor. Since sin(x) + sin(x + π) = 0, all of the beams from p₁ to p₂ would be cancelled with the beams from p₂ to p₃, to have diminished intensity. Similarly, if the two paths p₁ and p₃ are separated by integral multiple of 1/2 λ, then the beams of p₁ to p₂ and p₂ to p₃ are enhanced each other, creating the brighter fringes (or higher intensity). The incident angle, θ can be determined by considering a triangle formed by points, r, s and t. Similarly, Therefore, the maxima and minima of these fringes are given by the following,

$θ = {sin}^{- 1} (\frac{m λ}{a})$	m = 1, 2, 3, ...	22
$θ = {sin}^{- 1} (\frac{m λ}{2 a})$	m = 1, 2, 3, 4, ...	23

Most notable experiment is carried out by Young in 1801. Young observed interference pattern when the light is shone on a closely space double-slit as shown below (Figure 7).

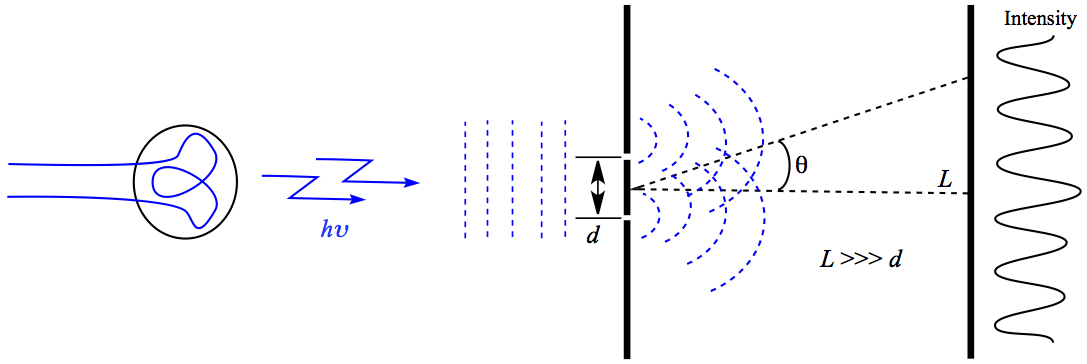
Figure 7. Double-slit Experiment by Young

The geometrical relationship between the wave length, slit geometry, and the angle of approaching beams are shown in Figure 8.

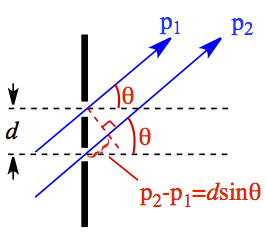
Figure 8. Configuration of Double-slit Experiment.

The brighter fringes are results of constructive interference while the darker fringes are from destructive interference. The interferences are given as a function of several variables,

$θ = {sin}^{- 1} (\frac{m λ}{d})$	m = 0, 1, 2, 3, ...	24
$θ = {sin}^{- 1} (\frac{λ}{d} (m + \frac{1}{2}))$	m = 0, 1, 2, ...	25

Eqn. 24 is for constructive interference and therefore gives rise to bright fringes, and Eqn. 25 is for destructive interference and thus to give rise to dark fringes in the double-slit experiment.

+ Intensity of Double-Slit Experiment

We examine the intesity of light coming through two slits with a distant source of monochromatic light. Let us examine electric field part of the light.

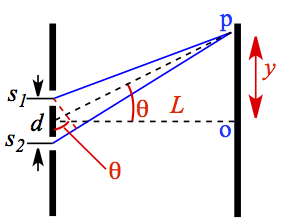
Figure C1. Configuration of Double-Slit Experiment.

The electric field at a point p, which forms the angle θ with the mid point of the two slits, is a superposition of E₁ and E₂ that are respectively orignated from s₁ and s₂ slits. Therefore,

E_{θ} = E_{1} + E_{2}

From before, the electric field can be written as sinusoidal, and we can write it as,

E_{i} = E_{i 0} sin (ω t + δ)

where E_i0 is the amplitude of ith electric field, ω is the angular frequency (ω = 2πλ), and δ is the phase factor. The electric field at point p from the two slits are then,

$E_{1} = E_{10} sin (ω t)$	C3
$E_{2} = E_{20} sin (ω t + δ)$	C4

We now express the phase factor in terms of θ. The small triangle formed by s₁, s₂, and the red dashed line is sinθ = d/δ, since the phase factor arises from the difference. If the two waves constructively interfere, sinθ = nλ, but if the two waves are destructively interfere, sinθ = nλ/2. Then, we can say that

δ = \frac{2 π}{λ} d sin θ

In order to obtain E_θ, we need to construct a phasor diagram, which is to construct a vector model relationship between amplitude, frequency and phase of sinusoidal functions. In our case, it looks like the one shown in Figure C2.

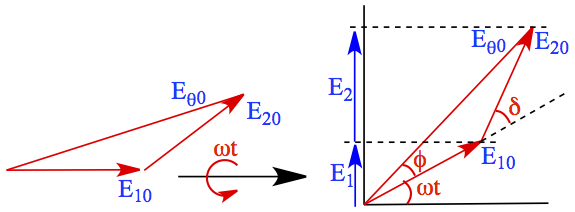
Figure C2. Phasor Diagram. We first place the amplitudes of E₁ and E₂ angled by the phase factor δ, with the resultant vector is E_θ. Then, it is followed by ωt rotation. The projection of the vectors on the y axis is the amplitude of E_θ.

Assumption: Since the light coming through the two slits should have equal amount of light (E₁₀ = E₂₀ = E₀).

The triangle 0-E₁₀ -E₂₀ is an isosceles triangle, then angle φ = δ/2 and E_θ0 is written,

E_{θ 0} = 2 E_{0} cos \frac{δ}{2}

Substitue Eqn. C6 into Eqn. C2 for θ, one gets

E_{θ} = 2 E_{0} cos \frac{δ}{2} sin (ω t + \frac{δ}{2})

The intensity, I_θ, is proportional to E_θ0², but the relative intensity is to compare I_θ with I₀ where θ = δ = 0. So,

\frac{I_{θ}}{I_{0}} = \frac{2 E_{θ 0}^{2}}{{(2 E_{0})}^{2}} = {cos}^{2} \frac{δ}{2}

Then, by substituting Eqn. C5, we obtain

\frac{I_{θ}}{I_{0}} = {cos}^{2} (\frac{π}{λ} d sin θ)

Let's take out assumption and generalize it.

In Eqn. C5, δ is dependent on sinθ. According to Figure C1, sinθ = y/L, therefore,

δ = \frac{2 π}{λ} d \frac{y}{L}

C10

Thus, Eqn. C9 can be rewritten as,

\frac{I_{θ}}{I_{0}} = {cos}^{2} (\frac{π}{λ} d \frac{y}{L})

C11

provided that L >>> y and L >>> d.