Matter and Energy
3 Phases of matter
Matter = has mass and occupies space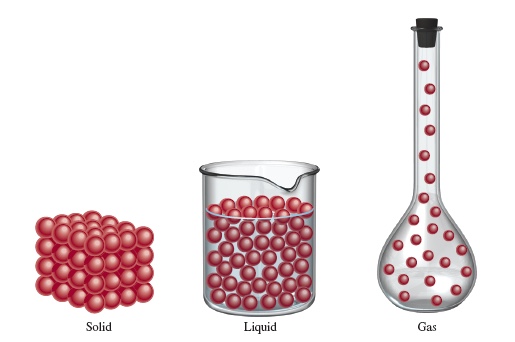 |
||
| Ice | liquid water | steam |
Energy
In order to convert one phase to another, it requires energy.Energy is an important concept that allow us to understand many of the phenomena we study in this course.
Energy can be in the form of:
Units of Measurement
Metric System — Health Professionals use metric system, in particular, SI Unit is adapted as the standard for scientific and medical purposes.
Length
For measurement of length, we use meter, m
Volume
Volume is measured in 3-dimensions (length, height, and width), and we use L (or liter)
Mass
Unit of mass is in SI unit is: kilograms, abbreviated as kg.
Temperature
There are 3 scales: Celsius (°C), Fahrenheit (°F), and Kelvin (K)
0°C = freezing point of water, 100°C = boiling point of water
0°F = freezing point of brine, 100°F = average human body termperature
Kelvin Temp = Celsius Temp. + 273.15
Kelvin is the SI unit of temperature, abbreviated as K.
Time
We know what time is, and we measure time in hours, minutes, seconds, days, months, etc. The SI unit is second, abbreviated as s.
Energy
Unit of energy is: joules, abbreviated as J. We will also see calorie (cal) in this course.
Scientific Notation
It is often encoutered the situation where a number is written in the following way, 0.0000034 g. These leading zeros are cumbersome, and sometimes ambiguity can be introduced when using the floating point (or decimal) notation. So, the standard practice in science is to use scientific notation.
The scientific notation is separated into two parts as
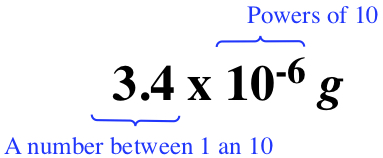
The second part is written in powers of 10. In this case, -6 is referred to as exponent. You know that 1/10 is 0.1, and further you know that 1/100 is 0.01. It can be written more mathematically
| number | notation & explanation | exponent |
|---|---|---|
| 1000000 | 106 | 6 |
| 100000 | 105 | 5 |
| 10000 | 104 | 4 |
| 1000 | 103 | 3 |
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 0.1 | 10-1 | -1 |
| 0.01 | 10-2 | -2 |
| 0.001 | 10-3 | -3 |
| 0.0001 | 10-4 | -4 |
| 0.00001 | 10-5 | -5 |
| 0.000001 | 10-6 | -6 |
Hint: It is easy to remember that
For example: 106 is 1 with 6 zeros after. Hence 1 000 000 (1 million)
For example: 10-5 is 0.000 01, as there are 5 zeros before 1
Measured Numbers & Significant Figures
Measured number always contains uncertainty!
Significant Figure = number of digits that you are able to measure, including last digit with estimation
So, in the following figure, how do you report?
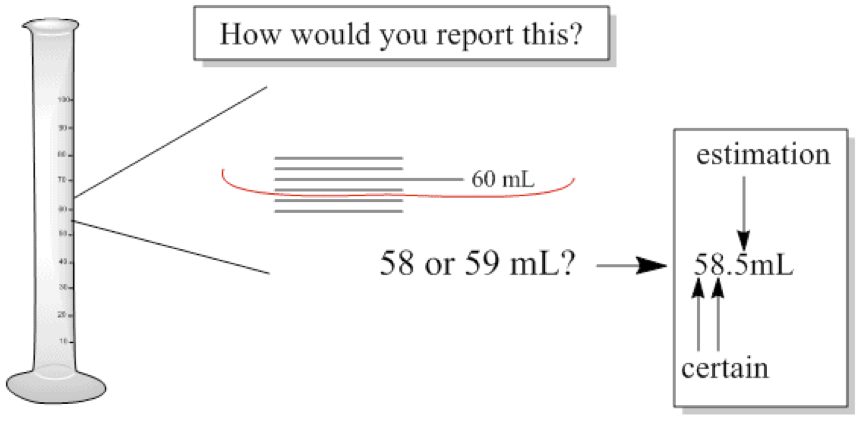
Since we can report 3 digits, it is said to have 3 significant figures.
Exact Numbers don't have significant figures associated with them. Exact numbers are definitions. For example, we know that 12 in = 1 ft. 1 ft is defined as 12 inches.
Significant Figures in Calculations
If not always, nearly all numbers you measured will be subjected to calculations, so it is quite important to know how to handle significant figures in the calculations.
In order to correctly use significant figures in calculations, you must know three things:
Rounding Off
Let's say that you have done some calculations, and your calculator reads, 0.98601904761905, and you know you have 2 significant figures. You would then report as 0.99.
Rules for Rounding Off
1. If the first digits to be dropped is 4 or less, then it and all following digits are simply dropped.
2. If the first digit to be dropped is 5 or greater, then the last digits
of the number is increased by 1.
Multiplication and Division
When two numbers are multiplied you retain the smaller significant figures of the two numbers.
Example: You're to multiply 0.843 x 0.3923. How do you report?
In the calculator, you should get 0.3307089. The first number, 0.843, has 3 significant figures, while the second number, 0.3923, has 4. So, the reported value should have 3 significant figures. Then, the value should be reported as 0.331, because the digit to be dropped is 7. Rule 2 applies, and 0 is increased to 1.
Example: Let's say that you are asked to calculate density, d from the mass, m, and volume, V, you measured.
Let's say that the mass was 10.3532 g and the volume was 10.5 mL. Then, you have, Now, you need to report the calculated values. How many significant figures can you report?
The numerator has 6 significant figures, while the denominator has 3. So, we have 3 significant figures. Then, the reporting value should be 0.986 g/mL. Rule 1 applied here.
Adding Significant Zeros
Often you encounter a situation that calculator give a whole number. For example, should give you 5 in the caluclator.
However, the numbers 42.5 has 3 and 8.5 has 2 significant figures. Therefore, overall significant figures in the reporting value is 2 sig. fig. So, you should report the value as 5.0 by adding trailing zero to 5.
Additon and Subtraction
Keep the least significant decimal places.
Say you are adding the following numbers, 4.111, 0.011, 2.01, and 2.2. So,
| 4.111 | 3 places after decimal point |
| 0.011 | 3 places after decimal point |
| 2.01 | 2 places |
| 2.2 | 1 places ← least decimal place! |
| | |
| 8.332 | |
| 8.3 | is the reported value |
Significant Figures in Calculations
Often times, it is very cumbersome to write 0.0005 g of prescription drug, many times over. So we can use milligram instead. Milli is a prefix to the gram quantity, and it means 0.001 or one thousandth. So, 0.0005 g = 0.5 mg. Easier to see, harder for workers to make mistakes.
You may know already some of the prefixes. How many bytes of disk do you have on your computer? If your computer is a laptop and relatively new, you may have 500 gigabytes (or Gb). Here giga is the prefix to byte, and it means 109, so 500 Gb = 500 000 000 000 bytes!!
Another example may be much more to our everyday life. You know 100 pennies will make a dollar. Therefore, 100 cent = 1 dollar, then 1 cent = 1/100 dollar.
Similarly, 100 cm (centimeter) = 1 m, and centi is the prefix to meter. The followingi table gives you the necessary prefixes.
| Prefix | Symbol | Multiplier |
|---|---|---|
| giga | G | 1 000 000 000 = 109 |
| mega | M | 1 000 000 = 106 |
| kilo | k | 1 000 = 103 |
| hecto | h | 100 = 102 |
| deka | da | 10 = 101 |
| 1 = 100 | ||
| deci | d | 0.1 = 10-1 |
| centi | c | 0.01 = 10-2 |
| milli | m | 0.001 = 10-3 |
| micro | μ | 0.000 001 = 10-6 |
| nano | n | 0.000 000 001 = 10-9 |
| pico | p | 0.000 000 000 001 = 10-12 |
| femto | f | 0.000 000 000 000 001 = 10-15 |
Example: How many gram are there in 2000 mg?
In the prefix milli indicates that the there are 1000 mg in 1 g. Or another way to put it, there are 10-3 g in 1 mg. Then, you can see that there are 2000 mg, and we know that 2(1000mg = 1g), therefore, 2 g.
Measuring Length
In measuring anything, we tend to use appropriate unit. For example, we use cm for height. We measure the direct distance from LIU Brooklyn campus to Statue of Liberty by km. A nurse may measure the length of skin lesion with cm scale. These are appropriate for its size, but you should know how to convert between m to the cm, km, etc.
Measuring Volume
Volume is a cube of length, meaning that (side) x (depth) x (height) = volume and 1 cm3 = 1 mL = 10-3 L is the starting point for conversions.

Measuring Mass
A body weight in metric system is generally obtained by using kg. 1 kg = 1000 g or 1 g = 10-3 kg. Medicine and its active ingredients are measured often by mg.
Writing Conversion Factors
Conversion Factor is a number associated with two units. For example, speed is a conversion factor between distance (miles) and time (hour). We write the highway speed limit in much of NJ is 55 miles/hr (miles per hour), as you know. What it really means is that for a car traveling 55 mi/hr, 1 hour is equivalent to 55 mi of distance. Thus, 55 mi = 1 hr.
What about 1 year? 1 year is defined as one circulation of Earth, which takes 365 days to complete. Further 1 day is defined as 1 rotation of Earth, which takes 24 hours. Hence 1 year = 365 days, 1 day = 24 hrs.
Above shows how we calculate intuitively. However, if the calculation involves little more twist, it is not easy to come up with the answer. So, here we'll show you how to do this more systematically.
Dimensional Analysis (takes thinking away from calculations!)
I mean it. When you get used to this type of calculations, you don't have to think hard to arrive at answers. By simply setting up a calculation, as prescribed below, you get to do conversions in no time!
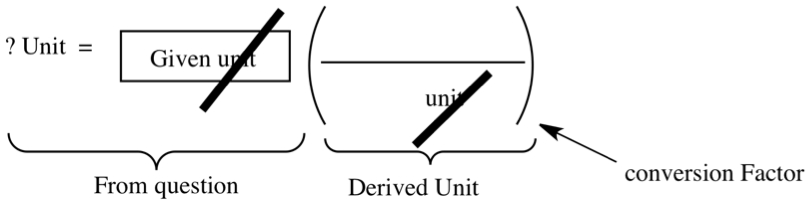
It is a restatement of conversion problem in English into mathematical language. Let's use above example of highway speed in Jersey. Let's ask ourselves the following in order to explain the figure above:
The question mark and unit, ?unit is the unit you are converting to. So, in the question, it would be, "How many miles?"
| ?mi |
An equal sign, = is the same as "can you travel", or in other problems, a phrase such as "are there" can be substituted for the equal sign.
| ?mi = |
Givenunit is where you place the number and its unit that is given to you. The unit is generally a fundamental unit, and it should not be a derived unit, consisting of two or more fundamental units. In the current example, the given is an hour. There is another number in the question, 55 mi/hr, the speed. The speed is the ratio between 55 mi and 1 hr, therefore considered to be derived unit.
| ?mi = 1 hr |
The last part is to place an parenthesis and divisor inside. In the parenthesis, you place what is referred to as conversion factor, which must have the same unit as the unit in the given.
The game we play here, is that you need to cancel out the unit of the given with the unit appeared in the denominator inside the parenthesis. In this example, 55 mi/hr is the conversion factor, since mi and hr appear in one unit. Furthermore, it is an equivalent statement of: 55 mi = 1 hr. If we place 1 hr in the denominator so that we can cancel the hr in the given, the left over (55 mi) must be on the numerator.
|
As you can see, since we cancel the hr units, you are left with the mi unit, which is what we are looking for! It can only mean; you're done! Now all you need is to calculate the answer.
What about the folloing?
|
|
Do you see the pattern? As you can see in the two examples above that the placement of 55 mi depends on what the given is. Again, the rule is that the denominator in the parenthesis must be canceled with the given unit, and the numerator in the parenthesis is dictated by the denominator. So, it is very mechanical. This method takes thinking out of the problem solving!! Try it out!!
Metric Conversion Factors
Above mentioned prefixes is used to convert within metric system. So, for example, 1 km = 1000 m, 100 cm = 1 m, 1 μm = 10-6 m, etc.
Example: Revisiting: How many g are there in 2000 mg.
We can cast the question into dimensional analysis as
Example: How many km are there in 250 m?
Since 1 km = 1000 m, and using dimensional analysis, you should get
Metric-US System Conversion Facotrs
Here in the table below, common units we use and their conversion factors are listed.
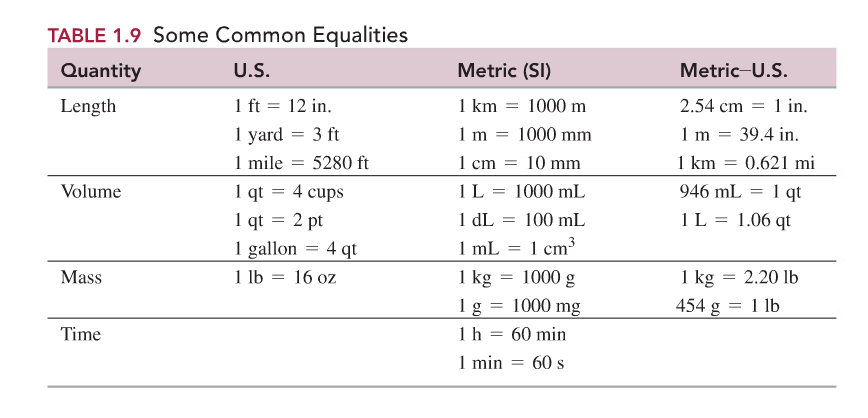
Example: How many m are there in 250 ft, if 1 in = 2.54 cm?
So, we need m from ft, given the conversion between in and cm. Again, you can treat this nothing more than dimensional analysis. So, write down as you state the problem:
We need to cancel ft, but I only know 12 in = 1 ft. If I use that, then:
Now the inches is converted to cm, by using 1 in = 2.54 cm:
All you need to do now, is to convert cm into m, i.e. 100 cm = 1 m: This give the final result:
Density, Specific Gravity, and Specific Heat
Density is given as the ratio between mass and volume, given by the following:
Density can have many different units, g/mL, g/L, kg/L, μg/mL, g/cc, etc.
Water has density of about 1 g/mL, depending on temperature. Generally, solid has higher density than water, therefore when a metallic object is placed in water, it sinks.
What abou ice? Ice is the frozen or solid form of water. Water is peculiar because the solid is less dense than its liquid form. This is why ice floats on top of water.
Generally, specific gravity is measured by a hydrometer, looks like the following picture.
Density of Solid
You can measure density of solid substance in few different ways.
- You can first weigh the sample on a balance to record its
mass.
- You fill water to a graduated cylinder to some amount, and
record.
- Place the substance in to the graduated cylinder, and
re-measure the volume.
- The difference between the two volumes
gives the volume of the substance.
Example: The density of bone is 1.90 g/cm3. How many cm3 are there if the bone weighs 500 g?
The way to start is, again, to convert the sentence into an equation. Then, look for conversion factor. In this case the bone density is the conversion factor.
Specific Gravity
Specific Gravity is the ratio of density of some substance with density of water. Density of water is about 1 g/mL depending on the temperature. Hydrometer measures the specific gravity of substance. You may have seen it in homebrewer's shop. It is basically to measure the alcohol content of in the fermentation process.
Specific Heat
Specific heat is the amount of heat energy required to raise the temperature of 1 gram of the substance by 1°C.Usually, we use the specific heat of water to be: Calculations involving specific heat.
Example: The specifi heat of gold is 0.0310 cal/°Cg. How many cal is required in order to raise 10.0g of gold by 5°C?
In this case the conversion factor is specific heat, and the meaning is given as
So, we set the dimensional analysis as Then, we get
Temperature Conversions
You can use either or for conversions.Example: What is the temperature 212°F in °C?
We can use and we substitute 212°F into T(°F), then Then, T(°C) = 100°C.
Extra Questions
Extra 1: What is the distance in miles you travel when you spent driving for 35.5 min. at 70.0 mi/hr?
Extra 2: What is the time in minutes you spent when you drive a car for 2.5 mi. at the speed of 100.0 mi/hr?
Extra 3: What is the mass in g if you have 20.0 mL with its density being 0.500 g/mL?
Extra 4: What is the volume in L if you have 20.0 g of a metal with its density of 8.7 g/mL?
Extra 4: Convert 20.1 nm into cm.
Extra 4: Convert 20.1 in into m, if 2.54 cm = 1 in..