Chapter 1 Chemistry: The Study of Change

Chemistry

Study of "everything" — central science

Study of "change" — your textbook

Examples:
drugs
textiles
fabrication of computer chips
metabolism
many many more

My definition: "Study of behavior of e^- in atoms and molecules"

Below is a video of biological processes that occur in your body every single seconds of our lives. Each and every particles you see in the video are the molecules of biology. The fundamental inner working of life is definitively chemistry. Many of these images are based on the experimental results of looking into the details of specific biological processes. Pretty amazing stuff!

Traditional Fields of Chemistry
These are dissolving (or smearing) quickly because of collaboration and new research

Analytical	Quantitation of chemicals — many instrumentations
Biochemistry	Study of biological processes
Inorganic	Study of molecules containing all but carbon
Organic	Study of molecules containing carbon
Physical	Understand chemistry through physical means

Scientific Method

Scientific Method — obtained based upon experiments or observations

Processes in Scinece
Experimental observation → tentative explanation → hypothesis → Law

Law explains empirical facts.

For example. You will learn about gases in Chapter 9. In that chapter, three facts emerge from experiments:

Observation	English translation of Equation	Equation
When there are more gas, pressure is increased	Pressure P is proportional to amount n	P ∝ n
When temperature is icreased, so as pressure	Pressure P is proportional to temperature T	P ∝ T
when gas is compressed, pressure increased	Pressure P is proportional to recipical of volume1/V	P ∝ 1/V

↓ putting all these together

PV = nRT, Ideal Gas Law

Explains how gases behave.

Two levels of understanding: Law vs. Theory
Law = empirically derived
Theory = explains Law

Theory explains underlying mechanism at deeper and more fundamental level.

Therefore, colloquial "in theory" is not how we use theory in science. → MUCH DEEPER!

For example: Carbon has 4 bonds → Facts from experiments

↓
Quantum mechanics explains why carbon has 4 bonds.

Classification of Matter

Matter = occupies space and has mass

We can classify Matter into several levels, as shown in the following figure.

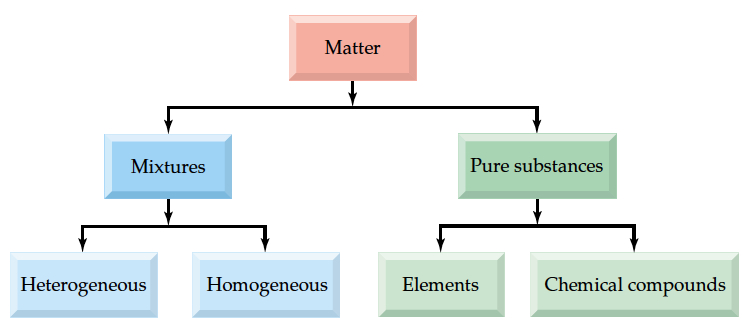
Substance = definite composition and distinct properties

Mixtures consist of Hetergenous and Homogeneous types. Heterogenous mixture is made up of two different and distinct phase separation between substances. For example, oil and vinegar layers of your favorite Italian dressing, have two distinct separation b/w oil layer and aqueous layer. On the other hand, homogenous mixture is like your softdrink before you open the bottle; can not distingush b/w water, sugar, and carbon dioxide, CO₂. Furthermore, the sugar and CO₂ are distributed throughout the water. Once you open the cap, however, it starts to fizzle, there you created phase separation, in this case you can consider it as heterogenous, but homogenous between water and sugar.

Pure substances can be classified by Elements and Chemical compounds. Chemical compunds are made up of one type of molecules. For example, water is a chemical compound having definite proportion, two Hydrogens and one Oxygen, represented by a chemical formula, H₂O.

Chemical Elements

Element (or atom) is the basic building block of chemistry.

Fundamental Substances — chemically unalterable or broken down to simpler substance

Over 90 different naturally occuring elements listed in the Periodic Table of Elements

Usually, we see the periodic table to be in the following way.

The 30 elements in two rows are separated, when combined it is represented in the fllowing way.

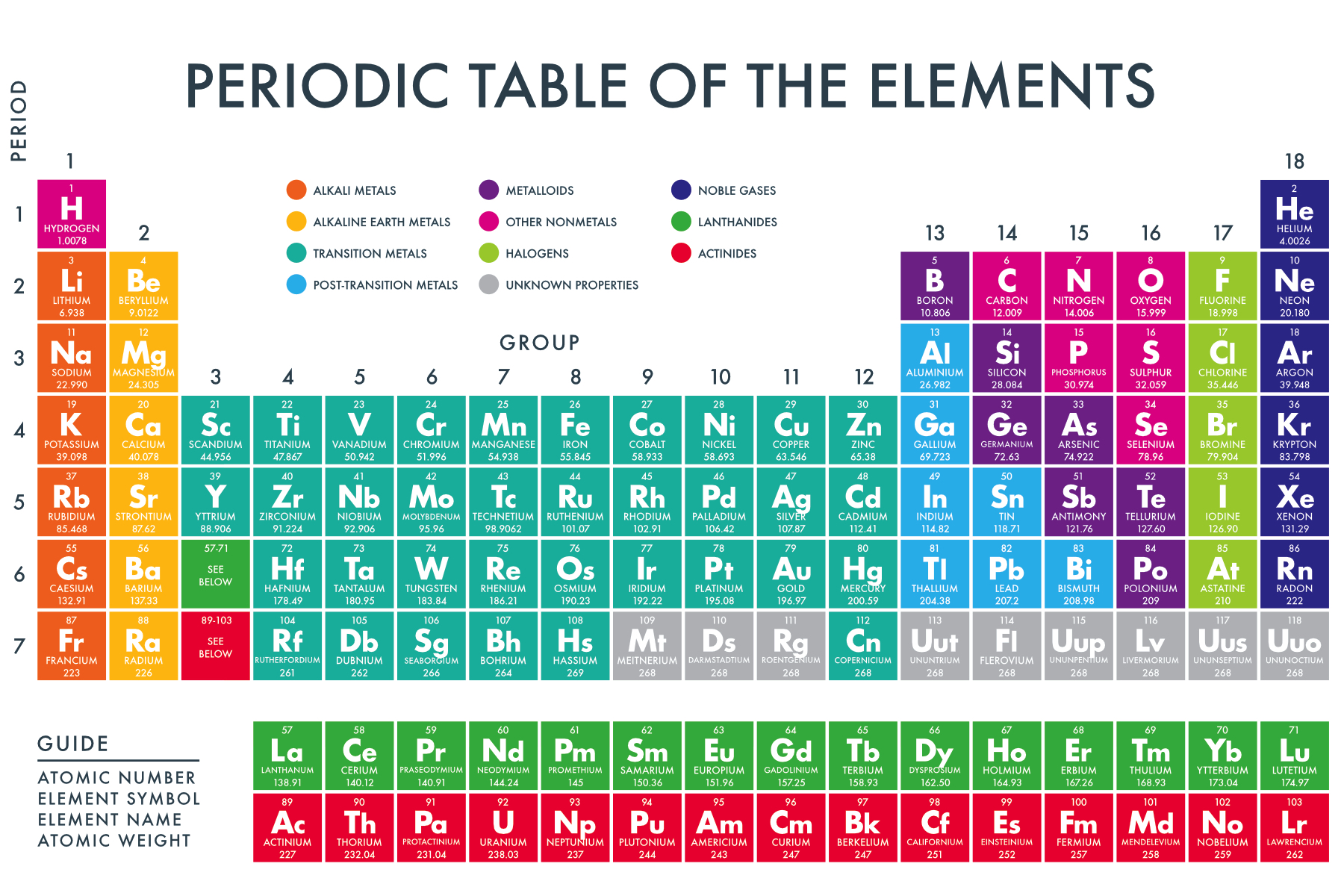
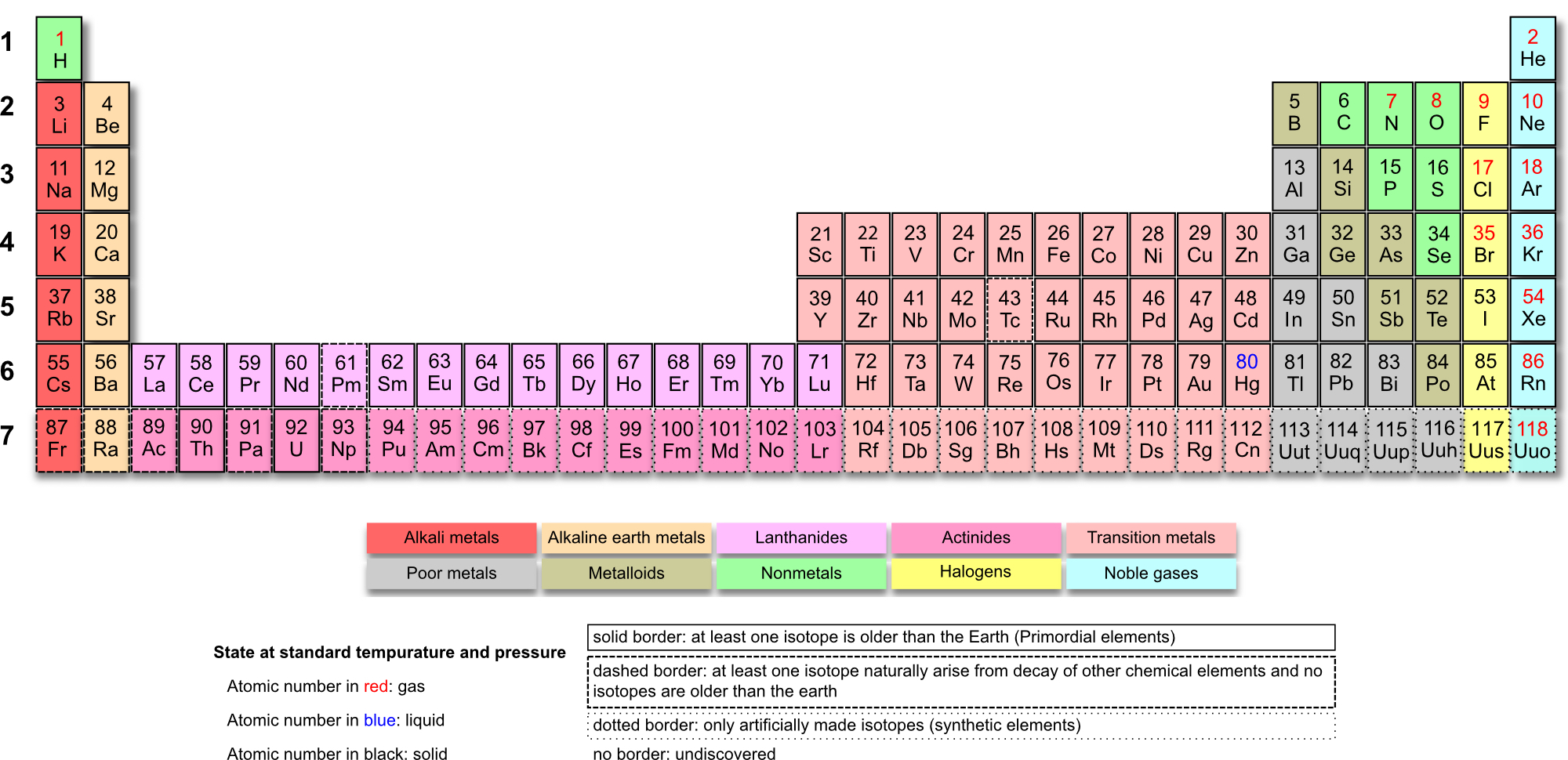
Group = elements in the same column
Period = elements in the same row

Each group has similar chemical properties

For example, Carbon belongs to group 14 so as silicon. Both can form up to 4 bonds.

Majority of elements are metals, i.e. conducts electricity and has shiny colors

Group 1	Alkali metals
Group 2	Alkali Earth metals
Groups 3 - 12	Transition metals
Groups 13 - 18	Main group elements
Elements 57 - 71	Lanthanides
Elements 89 - 103	Actinides
Group 15	Pnictogens
Group 16	Chalcogens
Group 17	Halogens
Group 18	Noble gas

Three States of Matter

Gas — No definite shape. Sparsely populated.
Liquid — No definite shape. Viscosity.
Solid — Definite shape. High density.

Example: Steam = gas, water = liquid, and ice = solid

Properties of Substances

Two types:

Physical property — change occurs w/o changing chemical compositions
Melting, boiling, density, solubility, among others

Chemical property — changes arrangement of atoms in molecule
From carbon, such as the pencil lead and fluorine gas → C-F bond containing Teflon — very tough material used for coating on a cooking surface of a pan — resistant toward acid and base

Another way: Extensive vs. Intensive properties

Intensive — independent of amount (or size)
Density, melting point, boiling point — good for ID

Extensive — depends on amount (or size)
Mass, volume, energy

!!! One can make extensive property into intensive by by another extensive property.

Mass (extensive) Volume (extensive)

→

Density (intensive) = Mass/Volume

Measurement

In this class, all quantities measured follows the standard unit, called SI unit. The following table lists some of the important ones.

Mass	kilograms	kg
Lenth	meter	m
Temperature	Kelvin	K
Amount of substances	mole	mol
Time	second	s
Electrical Current	ampere	A
Luminous Intensity	candela	cd

Below is the picture of the instruments used in measuring volumes.

From left to right,
Volumetri Flask, Graduated Cylinder, Pipet, and Buret
Notice that there is no beaker! Because for measuring a volume, beaker is not accurate enough!

Scientific notation — used to report measured values
It is quite nuisance to write a very large or very small number by using all those zeros. For example, 0.000 000 888. This can be written compactly by using scientific notation. 0.000 000 888 is expressed as 8.88 x 10^-7. In this notation, it is said to have 3 significant digits (these three numbers you have confidence in)

Prefixes for SI units

Larger prefix				Smaller prefix
Yotta	Y	1024		deci	d	10-1
Zetta	Z	1021		centi	c	10-2
Exa	E	1018		milli	m	10-3
Peta	P	1015		micro	μ	10-6
Tera	T	1012		nano	n	10-9
Giga	G	109		pico	p	10-12
Mega	M	106		femto	f	10-15
Kilo	k	103		atto	a	10-18
Hecto	h	102		zepto	z	10-21
Deka	da	101		yocto	y	10-24

Example: 1000 m = 1 km; 10 cm = 10⁴μm, etc.

Below is a movie called "Powers of Ten" gives you perspectives on distance that span of 40 orders of magnitude! (The order is the number that is raised on 10. Thus, if you have the spans over 100 times or 10², then we say that it spans two orders of magnitude.)

Unit Conversion

Converting the measured values into another unit. In this course, we will delve into this subject much deeper than just a simple conversion, such as

Conversion b/w mass: g → kg

Conversion b/w length: mile → cm

Temperature conversion: °F → °C

$$T\left({}^{\circ }C\right)=\frac{5}{8}\left(T\left({}^{\circ }F\right)-32\right)$$

You can covert the temperature in the Celsius scale to what is known as the absolute temperature scale.

$$T\left(K\right)=T\left({}^{\circ }C\right)+273.15$$ where K is called the Kelvin unit.

We will come back to the unit conversion little later with a powerful technique, called Dimensional Analysis.

Energy

Definition of energy: Capacity to do work or supply heat.

$$E=w+q$$ where w is the work, and q is the heat.

Another way, energy can be divided into kinetic energy, T, and potential energy, V, $$E=T+V$$ where $$T=\frac{1}{2}m{v}^2$$ with m = mass of object that is moving and its velocity is v.

The potential energy, V, is the energy depending on position. Intuitively, if I drop a ripe tomato from 30 cm in height vs. dropping from the roof of a building, you know you can get a bigger splatter by dropping from the rooftop. Before dropping, your tomato has potential energy (associated with gravity) that depended on the height.

Energy unit: we use joules (J) 1 J = 1 kg m² / s²

Chemists like to use another unit of energy: calorie (cal) 1 cal = 4.184 J

Handling Numbers

There is always error associated with your measurement.

Systematic error — inherent error, for example, in instrument

Random error — imprecise measurement, for example, your shaky hands!

Precision — degree of reproducibility
How a series of measurements deviate from each other
when deviation is small, it is said to be precise.

Accuracy — how close a measurement is to the true value

Significant Figuers

Degree of condidence — meaningful # of digits in reported values

Is it meaningful to say π=3.14159265359979? It really depends on how you carried out your measurement.

This is dependent on the number of digits that you are using in the calculations.

Before we move on, if the reported values appear as:
8.8 x 10^-2 g, it is said to have two significant figures.
8.80 x 10^-2 g, it is said to have three significant figures.
8.800 x 10^-2 g is said to have 4 sig fig, and so on.

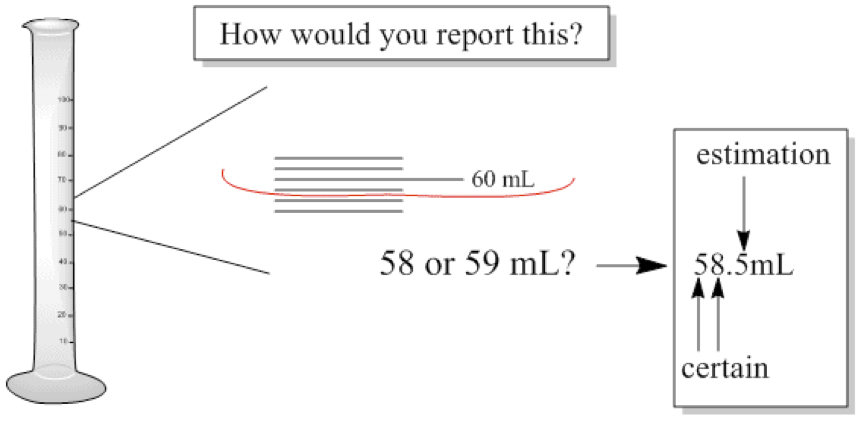
If a reported value is 800 m, is it 800 m ± 1 m? ± 10 m?
How would you report the following situation?

Significant figures in calculations

Multiplication and division — A x B = C. Use significant figure of whichever the smaller one (A or B) to the value of C.
Addition and subtraction — A - B = C. Use the smaller of the two decimal places of A or B in reporting C.

Rounding

If 0 - 4: If the first digit next to the last digit in the significant figure is 0 - 4, then remove all numbers smaller than the last significant digit.

2.4268 in 2 sig fig → 2.4

If 5 - 9: If the first digit next to the last digit in the significant figure is 5 - 9, then round up (add 1 to the last digit).

2.4268 in 3 sig fig → 2.43

Dimensional Analysis

Derived units — units that are composed of more than one fundamental unit. For example,

Velocity	m/s	miles/hr
Density	g/mL	kg/cm3
Concentration	mole/L	oz/gal
	Volume is a special case
Volume	m3	in3

We will do all kinds of conversions throughout this course. So, please follow closely!

We use dimensional analysis. The name of the game is to set up an equation such that you cancel out the given unit with conversion factors. It is more difficult to read it than to just do it!

The following figure shows the anatomy of dimesional analysis.

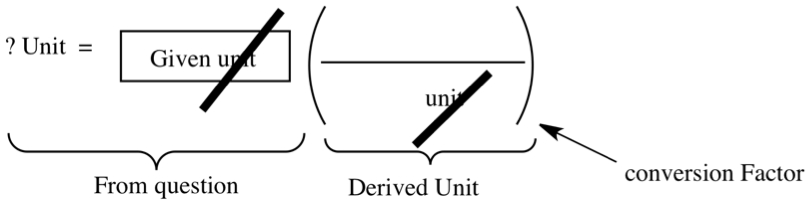
In this equation, the unit you are converting to appears on left with a question mark, and is equated to a certain given unit. In order for you to convert the given unit to desired one is to use a conversion factor, which usually comes from derived unit. If you place a right unit in the denominator in the parenthesis, you can cancel the unit with the given unit. By placing a unit in the denominator dictates what unit to put in the numerator.

Density and velocity are the typical examples of conversion factor. The former a has unit such as g/mL. Let's say that the density is 0.5 g/mL. It means for the purpose of dimensional analysis, 0.5g is equivalent to 1 mL. Or the speed limit on Major Deegan Expressway is 40 mi/hr in the Bronx. For our purpose, it has no deeper meaning, other than 40 mi is equivalent ot 1 hr. So, use derived units as your conversion factor.

Let's start with something very simple.

Converting length

So far, so good. Right?

Let's try using density.

Let's do little more complicated one.

How about this?

Let's try a difficult one.

What abut if we have the given to be the cube of the fundamental unit? In addition, the following question is very similar to Question 3 of the prelab in Density of Liquids and Solids lab.

Real-World Problem Solving

Back of an envelope or order of magnitude estimation are used in real-life situations. These are the ball park figures of accurate numerical calculations. Such is useful when trying to figure out the desired value in the context of the discussion.

Using the example immediately above on how many km there are in 1 light year, we can see that 4*2*6*6*3 x 10¹³ in the numerator, and the denominator is 10^-3. Thus combining the powers of 10, the value is 4*2*6*6*3 x 10¹⁰. So, 8*36*3 = 8*108 = 864 ≈ 900, and combining with the powers of 10, you get 900 x 10¹⁰ = 9 x 10¹².