Chapter 11 Intermolecular Forces and Liquids and Solids

Intermolecular Forces

Dipole Moment

Remember that Fluorine is has the highest value of electronegativity, χ? Due to electronegativity difference, Δχ, b/w two atoms, bond would polarize.

If the Δχ = 0, then the bond is said to be non-polar.
If the Δχ is non-zero, the bond is polar.

So for molecule N=O, we have
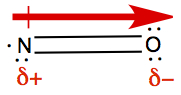As it is seen, arrow indicates the dipole moment of the bonds between N and O, and the arrow points toward more negative side, indicated with δ-, and the other end is more positive side, δ+. This is so because oxygen is closer to F in the periodic table than nitrogen.

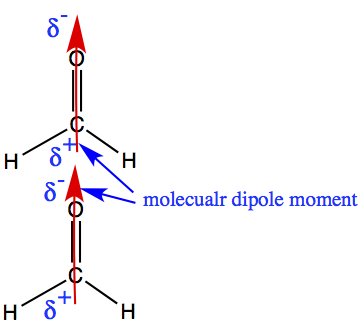
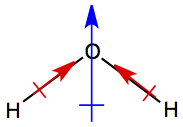Adding all Polarities of bonds → molecular dipole moment, μ

The bond dipole moments of O-H bonds (red arrow) in water points toward oxygen atom. When these two bond dipoles are added together, molecular dipole moment (blue arrow) is produced. As in the bond dipole, the direction the arrow is pointing has partially negative charge, and the opposite end has partially positive charge.

Example: Draw in polar bonds with arrows to show the bond dipole moments and molecular dipole moment of dimethyl ether (CH₃O CH₃), tetrafluoromethane (CF₄) and HCOCH₂CF₃.

In order to deduce dipole moments of molecule is to know the 3-D structure of the molecule. Then, draw in the bond dipoles (red arrows). We consider C-H and C-C bonds to be non-polar bonds, therefore we don't draw in the arrow for these bonds. After bond dipoles are drawn in, all bond dipole vectors are added, and the resulting vector is the molecular dipole moment (blue arrow ).

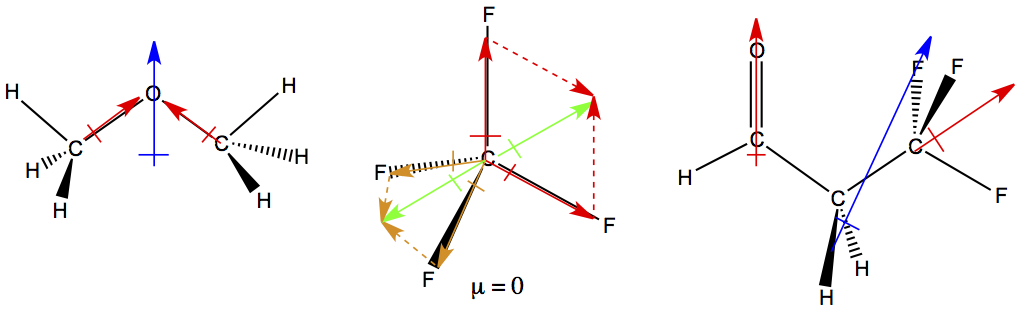
For CF₄, two of the red bond dipoles form a resultant green dipole in the plane of the computer monitor. For other two bond dipoles, with orange color, form another green resultant pointing in the opposite direction. And, they cancel each other, therefore the moleuclar dipole moment of CF₄ is zero.

Bond dipole is a Very Important Concept!! You'd have easier time knowing bond dipole and moleucular dipole moments in organic chemistry, Yes, in organic chemistry!

Intermolecular Forces

Forces b/w molecules

Forces responsible for condensing gas into liquid and liquid into solid

Forces responsible for making different compounds to have different melting point and boiling point.

Four types:

Ion-Dipole Interaction

Dipole-Dipole Interaction

Dispersion (London force, induced dipole interaction, or instantaneous dipole)

Hydrogen Bond

Ion-Dipole Interaction

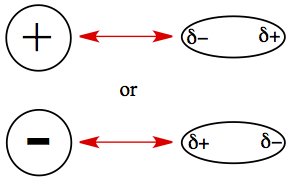Force exits between ion and molecule with permanent dipole moment. Cation is attracted to the partially negative side of the polar molecule, and anion is attracted to the partially positive end of the polar molecule.

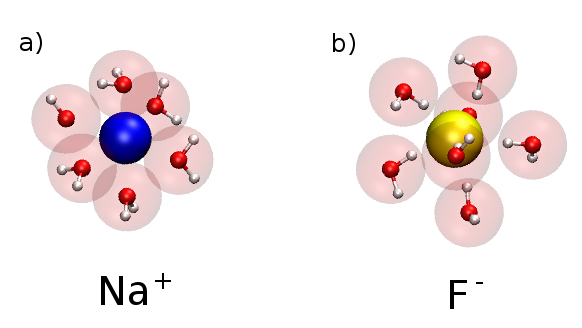Water surrounds Na⁺ ion in a) and F^- ion surrounded by water in b). The red sphere in water is the oxygen atom. Notice that the oxygen is pointing toward Na ion, and the hydrogen atoms point toward F ion.

Dipole-Dipole Interaction

Interaction b/w two molecules with permanent dipole moments. The partially positive charge side is attracted toward partially negative side, and vise versa.

So, if you have a bunch of N=O molecules, you'd see the packing of molecules as shown on the left diagram in the figure below. On the right diagram negative-negative interactions and positive-positive interactions, both represented by green arrows, are the repulsive interaction. So the structure is unstable. It'd eventually become the same packing as on the left.

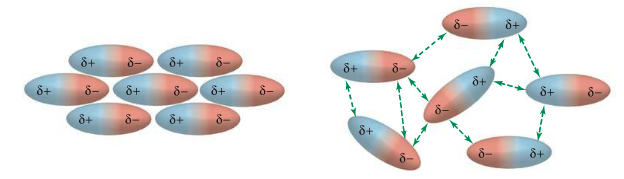
Dipolar vs non-dipolar interactions

	N₂	NO	O₂
Dipole(debye)	0	0.153	0
Mass (g/mol)	28	30	32
Boiling pt(K)	77	121	90

Dispersion Interaction

Consider non-polar non-ionic molecule A approaching non-polar non-ionic molecule B (top diagram on left).

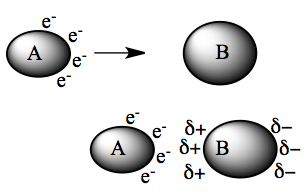
As they are close to each other, B sees the electrons on A, and the electrons on the left-side of B starts to avoid the approaching A (lower diagram on left). This induces polarity on molecule B, which in turn can polarize A as well. This is the source for the attractive force between non-polar non-ionic molecules.

If the molecule is easy to deform → said to be Polarizable.

Halogen	mp (K)	bp (K)
F₂	53.5	85.0
Cl₂	171.6	239.1
Br₂	265.9	331.9
I₂	386.8	457.5

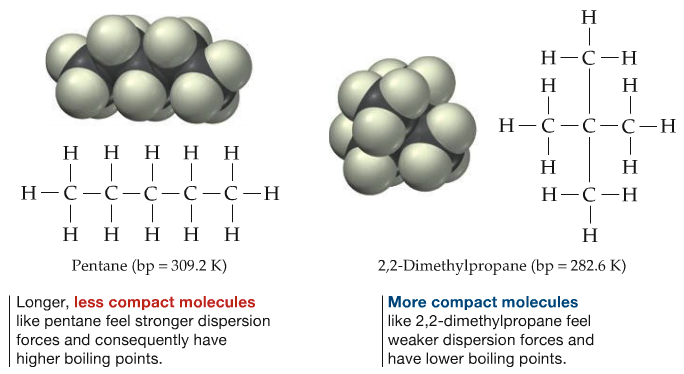As seen in Table above, both the melting point and boiling point are higher for molecules with higher polarizability, hence having stronger intermolecular force. Heavier the molecule → more polarizable.

Hydrogen Bonding

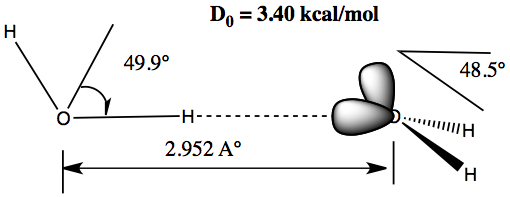
Sharing of hydrogen between two molecules

One must be a Hydrogen donor -- possessing H

One must be a Hydrogen acceptor -- possessing at least one pair of lone pair electrons

Each molecule must act as both the donor and acceptor.

The picture on the right is a dimer of water. The molecule on left is the H-donor and the one on right is the acceptor.

The shared hydrogen is co-linear with the lone pair-H-donor.

The binding energy for water dimer is quite small (3.4 kcal/mol). But, this is the force holding two strands of DNA.

Comparison of the strength of intermolecular forces

Force	Strength in kJ/mol	Strength in kcal/mol
Ion-Dipole	10 - 50 kJ/mol	2 - 12 kcal/mol
Dipole-Dipole	3 - 4 kJ/mol	0.5 - 1 kcal/mol
Dispersion	1 - 10 kJ/mol	0.2 - 2 kcal/mol
H-bond	10 - 40 kJ/mol	2 - 10 kcal/mol

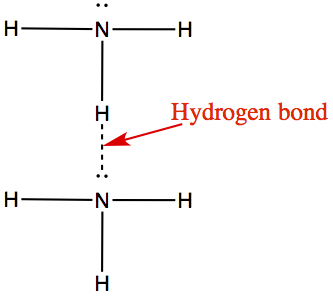
Example: What is the most important intermolecular force exit in each of the following liquid? Can you draw two molecules for each and show how they are aligned? 1) Liquid ammonia (NH₃, 2) C₆H₁₄, and 3) Formaldehyde (COH₂)

1) Liquid ammonia, NH₃, has lone pair electrons and H, therefore it can H-bond to each other. The two molecules can interact in the following way.

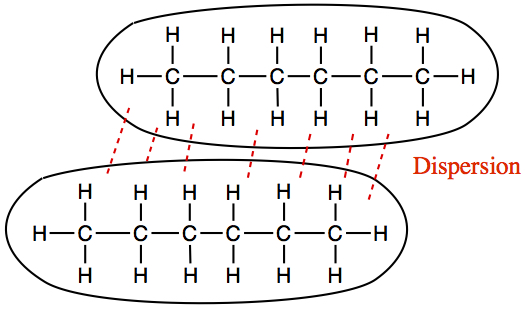
2) C₆H₁₄ (hexane) is non-polar and elongated molecule. So, it only has dispersion interaction. In order to liquify, two molecules must be aligned sideways as shown below.

3) Formaldehyde is a dipolar molecule. The dipole-dipole interaction entails lining up the two dipole moments as follows:

Liquid Properties

Surface Tension Energy needed to increase surface area (Cohesive energy)

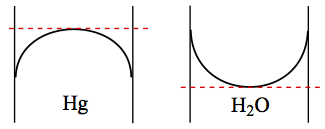The red dashed line is the meniscus you read for measurements, like measuring the volume of water with graduated cylinder.

Mercury side = Convex H₂O side = Concave

Hg Intxn with glass is weak H₂O Intxn with glass is strong

Cohesive Energy of Hg is stronger than intxn b/w Hg and glass Cohesive Energy is weaker than intxn b/w H₂O and glass

Clean waxed car → water beads up -- cohesion (or surface tension) wins

Dirty car → water spreads -- cohesion (or surface tension) wins

Structure of Water

Water is peculiar. Unlike most other liquid, its density in water is higher than the solid state (ice). You know ice floats on top of the water tells you exactly the fact. The reason for high density in water is in the structure of water. The image shown below is the structure of solid water, and they are completely hydrogen-bonded to each other.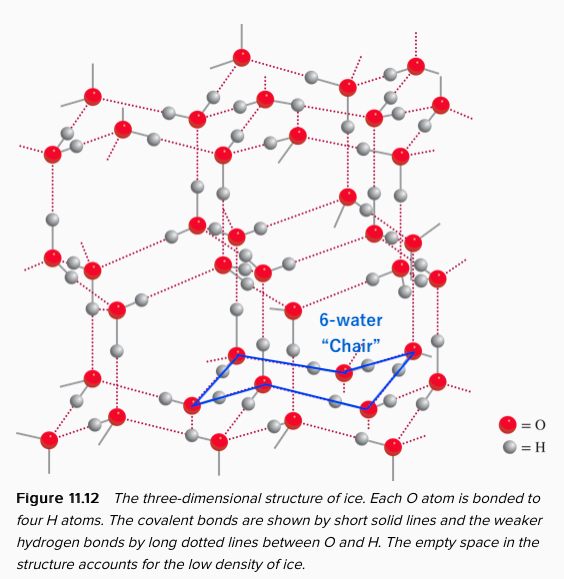

As you can see six water molecules form what appears to be chair-like structure in their hydrogen-bonded strucutre. The chair is stacked together in all three dimensions.

Crystal Structure

Two structural types of solids

Crystaline - ordered unit cells (repeating unit cell pattern) -- metal crystal, salt crystals

Amorphous - no long-range order -- glass, polymers

Types of Crystaline Solids

Types	Intermolecular Forces	Properties	Examples
Ionic	Ion-ion force	Brittle, hard, high-melting	NaCl, KBr, MgCl₂
Molecular	Dispersion, dipole-dipole, H-bond	Soft, low-melting, non-conducting	H₂O, Br₂, CO₂, CH₄
Covalent network	Covalent bonds	Hard, high-melting	diamond, SiO₂
Metallic	Metallic bond	Variable hardness and melting points, conducting	Na, Zn, Cu, Fe

X-Ray Diffraction

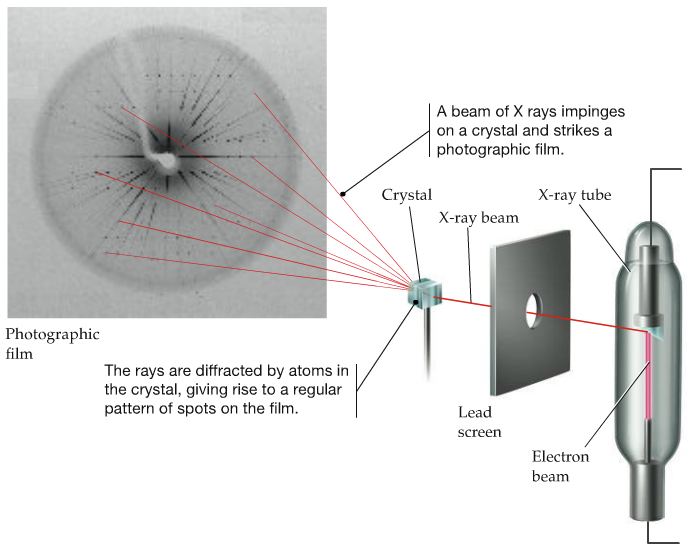
X-ray is used to determine the structure of crystal -- very important tool in Biochemistry -- Protein structures are determined this way. The structure of DNA was discovered by this technique.

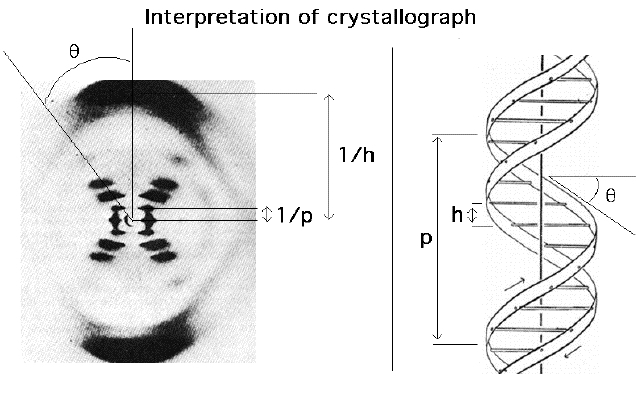Above diagram shows how the experiment is carried out. X-ray is irradiated onto a crystal. Then the diffraction pattern is photographed. This is the diffraction pattern of one form of DNA. As can be seen, the structural parameters are obtained from the diffraction pattern.

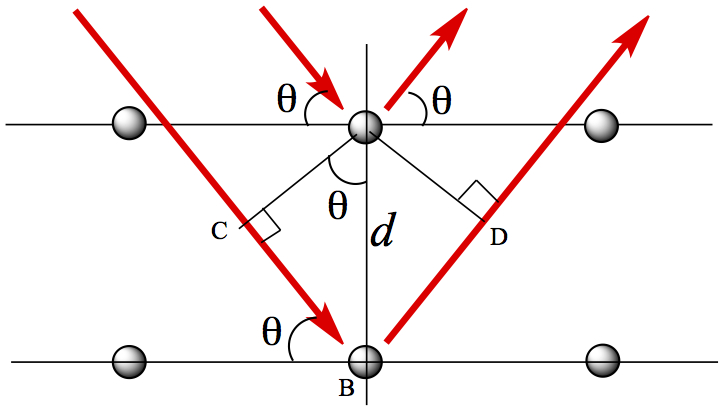
The red arrows from left to fall on atoms indicates incident X-ray, and the red arrows going away from atoms are the diffracted (outgoing) X-ray. The incident rays with the wave length, λ, on the 2^nd layer must travel extra distances covered by the lengths, C-B and B-D. The diffraction pattern only appears when the extra distances, C-B and B-D are integral multiples of λ

By using trigonometry, one can show the extra distnaces traveled is:

$C B = B D = d \sin θ$

Then, according to Bragg, the distance C-B and B-D is related to integral multiple of λ, thus one obtians the relationship between incident X-ray wave length and the structural parameter, d is given as

$d = \frac{n λ}{2 \sin θ}$

This is called Bragg equation.

Example: The distance between layers of a NaCl crystal is 282 pm. X rays are diffracted from these layers at an angle of 23.0 °. Calculate the longest wave length in Å.

Rearranging Bragg equation, we have

λ = 2 d \sin (θ)

Here, we have the longest wave length, therefore n = 1. The layer distance, is 282 pm, which is 2.82 Å, thus the wave length is

λ = (2) (2.82 Å) \sin (23.0) = 2.23 Å

Crystal Types

Crystalline solids have repeating unit → Unit Cell.

The repeating pattern of unit cells determine the structure of crystal.

Crystal packing

Crystal packing shows how the atoms are arranged in a crystal. There are four types:

Simple Cubic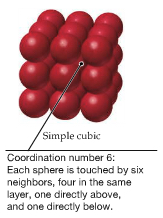
Body-Centered Cubic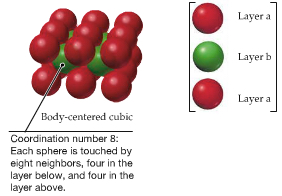
Hexagonal Closest-Packing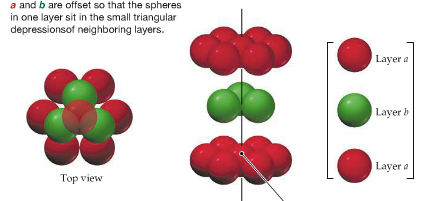
Cubic Closest-Packing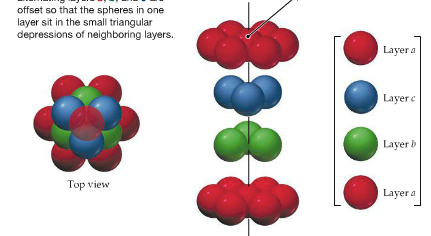

Unit Cells

Within the packing pattern, one can consider a unit of repeating cells, called unit cell, which contains fewest possible atoms. For example, simple cubic packing pattern can be considered to have a unit cell with the edge length a and contains 1/8 of atoms at each corner, which means there are 1 atom in the unit cell, as shown below. There are two other types of unit cell within the so-called simple cubic unit cell.

3 types:

Primitive Cubic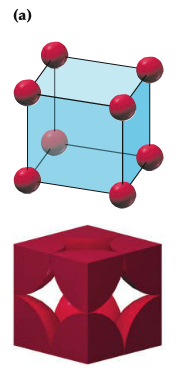
Body-centered Cubic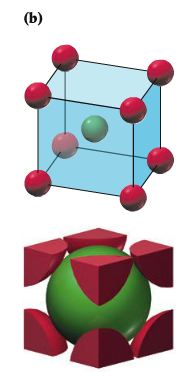
Face-centered Cubic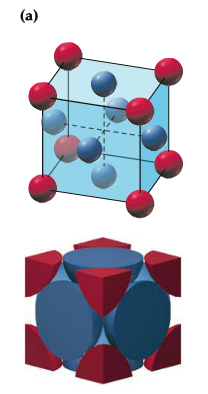

In the following diagram, the relationship between the edge length and atomic radius of monoatomic solid that packs in a simple cubic cells.

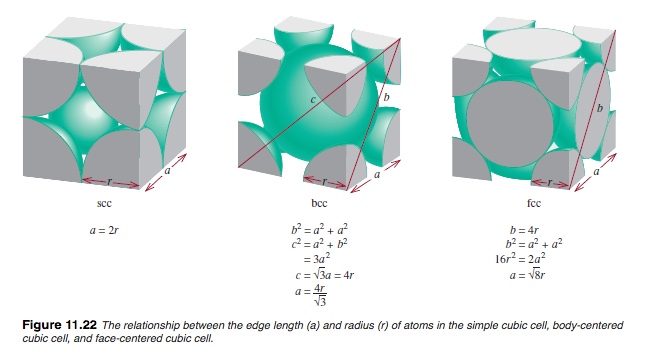
Example: What is the density of tungsten (W) in g/cm³ which assumes body-centered cubic packing? The atomic radius of W is 1.39 Å.

Using the above diagram, we can get the edge length, a, from the atomic radius, r, by using the relationship shown in the diagram above, and it is

a = \frac{4 r}{\sqrt{3}}

Therefore, a = 4(1.39 Å)/√3 = 3.210 Å. So the volume of the unit cell is (3.210 Å)³.

We need the mass of W atoms in the unit cell. We can obtain it by counting the number of atoms in the cell and convert them into g, using Avogadro's number.

There are two W atoms in the cell. Then, $? g_{W} = 2_{W} (\frac{1 m o l_{W}}{6.022 \times 10_{W}^{23}}) (\frac{183.84 g_{W}}{1 m o l_{W}}) = 61.0 \times 10_{g_{W}}^{- 23}$ The volume is (3.210 Å)³, but it needs to be converted to cm³. $? c m^{3} = {(3.210 \overset{\circ}{A})}^{3} {(\frac{1 m}{10^{10} \overset{\circ}{A}})}^{3} {(\frac{100 c m}{1 m})}^{3} = 33.08 \times 10^{- 24} c m^{3}$ The density, then is, $d = \frac{m}{V} = \frac{61.0 \times 10_{g_{W}}^{- 23}}{33.08 \times 10^{- 24} c m^{3}} = 18.4 g / c m^{3}$ The measured density is 19.25 g/cm³.

Example: 11.40. Barium metal crystallizes in a body-centered cubic arrangement. The unit cell edge length is 502 pm, and the density of the metal is 3.50 g/cm³. Calculate Avogadro's number.

Avogadro's number is relating the atomic mass unit (amu) to gram unit. It means that so many amu would make up to be one gram. Remember that in Chapter 3, we saw that $1 a m u = 1.660539 X 10^{-24} g$ And, we said that the reciprocal of the gram value was the Avogadro's number. It means then the value $\frac{1 a m u}{g} = 6.022141 X 10^{23} = N_{A}$ Therefore, we seek this ratio. First, we obtain amu/cm³, then we obtain g/cm³. Because we can calculate these.

Since we already know the density, which is 3.50 g/cm³, we just need to convert the unit cell dimension to amu per cm³. Then, take a ratio between them to obtain the desired amu to g ratio.

$?_{c m^{3}} = {(502 p m)}^{3} {(\frac{1 m}{10^{12} p m})}^{3} {(\frac{10^{2} c m}{1 m})}^{3} = 1.265 \times 10^{-26} c m^{3}$ Since there are two barium atoms in the cell, the mass is 2×137.33 amu in the unit cell which makes the density to be $d = \frac{274.66 a m u}{1.265 \times 10^{-26} c m^{3}} = 2.1712 \times 10^{24} a m u / c m^{3}$ Avogadro's number is given by the ratio of atomic mass unit (amu) to the gram quantity (amu/g) according to Chapter 3. The ratio of densities (amu/cm³ to g/cm³) would give us the desired value of amu/g. $N_{A} = \frac{2.1712 \times 10^{24} a m u / c m^{3}}{3.50 g / c m^{3}} = 6.212 \times 10^{23} a m u / g$ or $1 a m u = 1.6605 \times 10^{-24} g$ Not too bad of agreement.

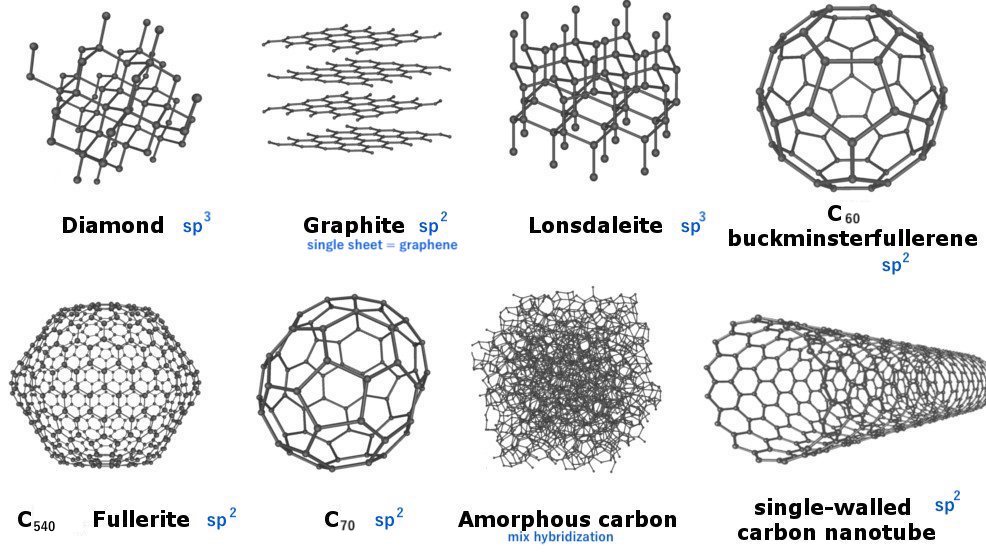
Allotropes = same element with different structural forms

Carbon has 40 allotropes! Graphite (graphene → Nobel Prize for synthesizing), Buckminsterfullerene or bucky ball (Nobel for determining structure), Bucky tubes, diamond, etc.

Some of the allotropes of cabon are shown here:

Phase Changes

Phase Change

A few names associated with phase change:

Fusion (melting)	solid → liquid	Δ H >0
Freezing	liquid → solid	Δ H < 0
Vaporization	liquid → gas	Δ H > 0
Condensation	gas → liquid	Δ H < 0
Sublimation	solid → gas	Δ H > 0
Deposition	gas → solid	Δ H < 0

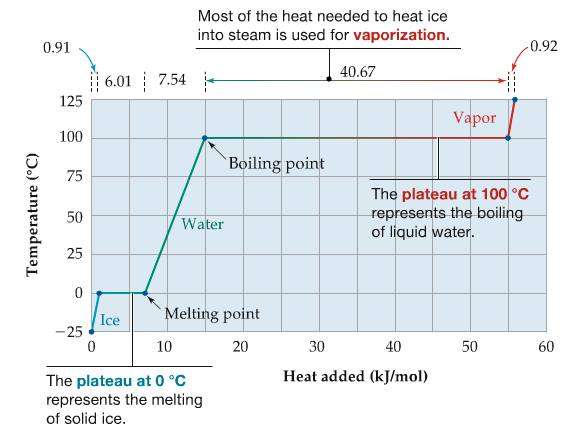
This is a plot of heating curve of water. Plotted is the temperature of water by adding more heat (energy) to the water. Notice there are two plateaus at melting point and at boiling point.

In order for you to make 100° liquid H₂O to 100° gas H₂O (steam), it needs about 40 kJ/mol of energy.

This is the heat of vaporization, ΔH_vap = 40.67 kJ/mol.

Similarly, you see less than 10 kJ/mol is needed to melt ice into liquid → heat of fusion, ΔH_fus = 6.01 kJ/mol

Example: How much heat (in kJ) is needed to convert 900 g of ice at -20°C to steam at 120°C, given that specific heats of ice and steam are 2.03 J/g°C and 1.99 J/g°C, respectively.

The total heat required is given by contributions from bringin ice to 0°C, melting ice, heating liquid to 100°C, converting water to steam, and bringing steam to 120°C, which can be shown in the following: $q_{t o t a l} = q_{i c e} + q_{f u s} + q_{w a t e r} + q_{v a p} + q_{s t e e m}$ The contributions for q_ice, q_water, and q_steam, needs $q = m c Δ T$ , while the contributions from q_fus and q_vap are to compute q from the heats of fusion and vaporization.

$q_{i c e} = m_{i c e} c_{i c e} Δ T = (900 g) (2.03 J / g ° C) (20 ° C) = 36540 J = 36.540 k J$ $q_{f u s} = 900 g (\frac{1 m o l}{18.016 g}) (\frac{6.01 k J}{1 m o l}) = 300.23 k J$ $q_{w a t e r} = m_{w a t e r} c_{w a t e r} Δ T = (900 g) (4.184 J / g ° C) (100 ° C) = 376560 J = 376.560 k J$ $q_{v a p} = 900 g (\frac{1 m o l}{18.016 g}) (\frac{40.67 k J}{1 m o l}) = 2031.7 k J$ $q_{s t e a m} = m_{s t e a m} c_{s t e a m} Δ T = (900 g) (1.99 J / g ° C) (20 ° C) = 35820 J = 35.82 k J$ $q_{t o t a l} = (36.54 k J) + (300.23 k J) + (376.56 k J) + (2031.7 k J) + (35.82 k J) = 2780.85 k J = 2.78 \times 10^{3} k J$

Liquid Vapor Equilibrium

Vapor Pressure ← Dyanmic equilibrium b/w liquid and gas

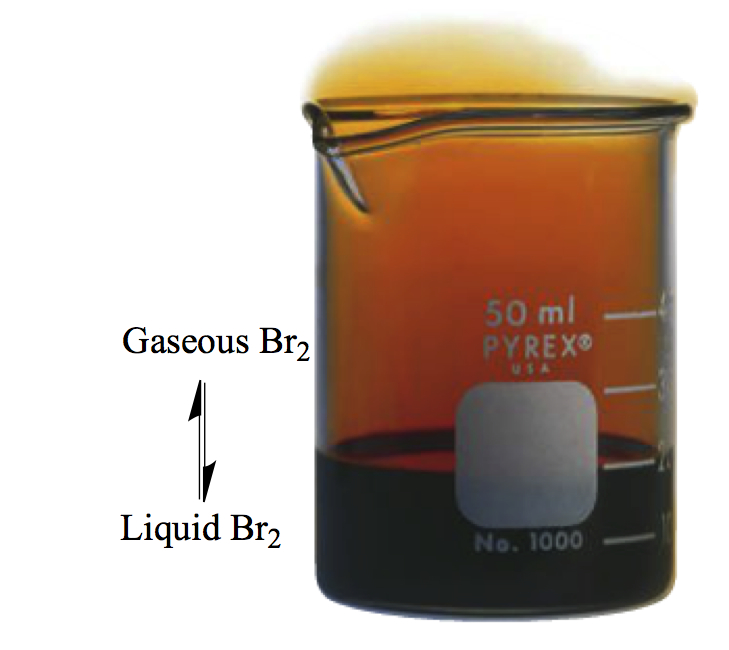
Over the surface of liuquid bromine, you see vapor of gaseous bromine. Liquid and gas establish a so-called dynamic equilibrium.

Rate_in = Rate_out

Rate of Br₂(g) goes in to the liquid is equal to the Rate of Br₂(l) becoming gas.

Higher the temperature → Higher the vapor pressure

Higher T → Larger E_K → Easier to overcome intermolecular intxns.

T > 0 K, there is always vapor exists over solid or liquid.

Clausius-Clapeyron Equation

If you plot P_vap as a fxn of T, you get a picture on the left

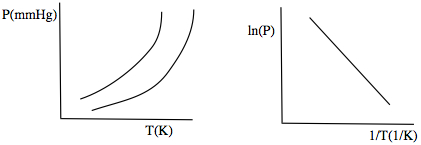
But if you plot ln(P) vs. 1/T, instead, the curve becomes linear!

Linear equation is easier to work with!!!

The relationship b/w ln(P) and 1/T is,

$\ln (\frac{P_{2}}{P_{1}}) = \frac{- Δ H_{v a p}}{R} (\frac{1}{T_{2}} - \frac{1}{T_{1}})$ In this equation, R = 8.314 J/molK is used. It means that for T, we should be using Kelvin unit. For pressure, you can use whatever the unit as long as P₁ and P₂ have the same unit. Δ H_vap is the heat of vaporization (for water, it is 40.67 kJ/mol as we discussed above).

Example: Denver is known as the Mile High City. If the barometric pressure is measured to be 0.837 atm, what is the boiling point of water in Denver?

We know water boils at 100°C at sea level at which barometric pressure is 1.00 atm. Let's assign P₁ = 1.00 atm and T₁ = 100°. So, we are solving for T₂. Then,

$\begin{array}{l} \frac{- R}{Δ H_{v a p}} \ln (\frac{P_{2}}{P_{1}}) = \frac{1}{T_{2}} - \frac{1}{T_{1}} \\ \frac{1}{T_{2}} = \frac{R}{Δ H_{v a p}} \ln (\frac{P_{1}}{P_{2}}) + \frac{1}{T_{1}} \\ T_{2} = \frac{1}{\frac{R}{Δ H_{v a p}} \ln (\frac{P_{1}}{P_{2}}) + \frac{1}{T_{1}}} \end{array}$

Substitute #'s in. $T_{2} = \frac{1}{\frac{8.314 \frac{J}{m o l K}}{40.67 \times 10^{3} \frac{J}{m o l}} \ln (\frac{1.00 a t m}{0.837 a t m}) + \frac{1}{373.15 K}} = \frac{1}{3.6374 \times 10^{- 5} / K + 2.6799 \times 10^{- 3} / K} = \frac{1}{2.7163 \times 10^{- 3} / K}$

T₂ = 368.15K, or 95.0°C.

We can go the other way around:

Example: Denver is known as the Mile High City. If water boils at 95.0°C in Denver, what is the barometric pressure?

Again, we know water boils at 100°C at sea level and at 1.00 atm barometric pressure. We can make T₁ to be the 100°C and P₁ to be 1.00 atm. Then, T₂ to be 95.0°C and we solve for P₂. $\ln (\frac{P_{2}}{P_{1}}) = \frac{- Δ H_{v a p}}{R} (\frac{1}{T_{2}} - \frac{1}{T_{1}})$ Exponentiate both sides of the equation, we get $\frac{P_{2}}{P_{1}} = e^{\frac{- Δ H_{v a p}}{R} (\frac{1}{T_{2}} - \frac{1}{T_{1}})}$ $P_{2} = P_{1} e^{\frac{- Δ H_{v a p}}{R} (\frac{1}{T_{2}} - \frac{1}{T_{1}})}$ $P_{2} = (1.00 a t m) e^{\frac{- 40.67 \times 10^{3} J / m o l}{8.314 J / m o l K} (\frac{1}{368.15 K} - \frac{1}{373.15 K})} = 0.837 a t m$

Phase Diagram

Phase diagram shows phases of substance as a function of temperature and pressure.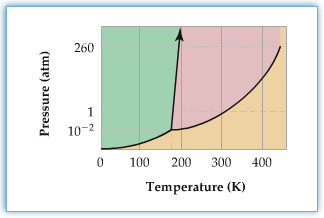

Each solid lines represent phase boundary. For example, the line in the diagram with an arrow is a phase boudnary b/w solid and liquid.

We know:

At relatively high pressure and low temperature, substance is solid

Keeping the pressure relatively high, and increase the temperature to higher, substance becomes liquid

If the temperature is further increased liquid becomes gas

So, the left-most (green region) is solid, middle part (pink region) is liquid, and bottom part (yellow region) is gas.

Important points and processes on phase diagram

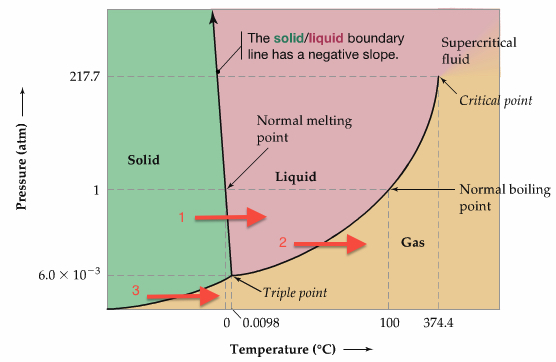
Few important Points on the Phase Diagrams:

Normal Melting point = melting point measured at 1 atm

Normal Boiling point = boiling point measured at 1 atm

Triple Point = all three phases co-exists

Critical point = Can't be condensed to liquid by pressurizing further; Can't be vaporized with higher temperature

Supercritical Fluid is used to decaffinate coffee beans.

Important Processes:

1 = Fusion (melting) ⇆ Freezing

2 = Vaporization ⇆ Condensation

3 = Sublimation ⇆ Deposition

Mercury side = Convex	H₂O side = Concave
Hg Intxn with glass is weak	H₂O Intxn with glass is strong
Cohesive Energy of Hg is stronger than intxn b/w Hg and glass	Cohesive Energy is weaker than intxn b/w H₂O and glass


Above diagram shows how the experiment is carried out. X-ray is irradiated onto a crystal. Then the diffraction pattern is photographed.	This is the diffraction pattern of one form of DNA. As can be seen, the structural parameters are obtained from the diffraction pattern.

Chapter 11 Intermolecular Forces and Liquids and Solids

Properties of Liquids and Solids. Intermolecular Forces

Intermolecular Forces

Dipole Moment

Intermolecular Forces

Ion-Dipole Interaction

Dipole-Dipole Interaction

Dipolar vs non-dipolar interactions

Dispersion Interaction

Hydrogen Bonding

Comparison of the strength of intermolecular forces

Liquid Properties

Structure of Water

Crystal Structure

X-Ray Diffraction

Crystal Types

Crystal packing

Unit Cells

Allotropes = same element with different structural forms

Phase Changes

Phase Change

Liquid Vapor Equilibrium

Clausius-Clapeyron Equation

Phase Diagram

Important points and processes on phase diagram