Chapter 12 Solutions and Their Properties

Solutions

Solution is a two-component system.

Smaller component = solute

Larger component = solvent

Energy Changes and the Solution Process

When some solute spontaneously dissolves into solvent, energetics must become favorable. Such energy is called Gibb's free energy, given by the following.

ΔG = ΔH - TΔS

governs the dissolution process. So there are two components:

Enthalpy (Δ H part)
Entropy (Δ S part)

In all cases, Entropy term is favorable for making a solution. This is because a solution is more disorderly than the separate solute and solvent.

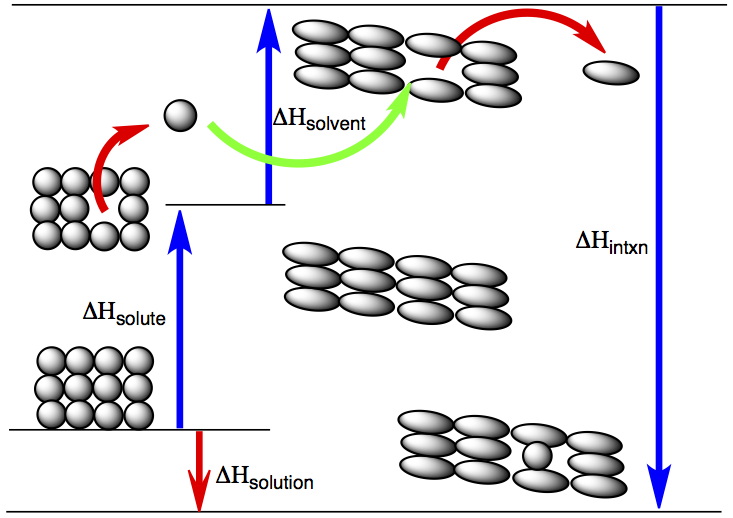
Exo- or endothermicity of the process of dissolving (enthalpy of solution) is explained by the following diagram.

In order to pull out a solute molecule from its crystaline solid takes energy (ΔH_solute). Always, ΔH_solute > 0

The solvent also has to make a room for incoming solute molecule. The process also takes energy (ΔH_solvent). Always, ΔH_solute > 0

The interactin b/w solute molecule and solvent is generally attractive, but varies in strength (ΔH_intxn). In this picture, ΔH is larger (more negative) than the magnitude of ΔH_solute + ΔH_solvent. Therefore, overall dissolution process is exothermic. Exothermicity (or endothemicity) really depends on the interaction b/w solute and solvent.

Like dissolves like. Similar molecules have similar groups (substituents), therefore they have similar intermolecular forces so that they can dissolve each other.

Here is the solubility of alcohols in water. Alcohol has OH group, which can hydrogen-bond to water to dissolve. As the chain length gets longer, it becomes more non-polar (fat-like) thus reducing the solubility.

Name	Formula	Solubility in water
Methanol	CH₃OH	Completely
Ethanol	CH₃CH₂OH	Completely
Propanol	CH₃CH₂CH₂OH	Completely
Butaanol	CH₃CH₂CH₂CH₂OH	74g/100g H2O
Pentanol	CH₃CH₂CH₂CH₂CH₂OH	27g
Hexanol	CH₃CH₂CH₂CH₂CH₂CH₂OH	6 g
Heptanol	CH₃CH₂CH₂CH₂CH₂CH₂CH₂OH	1.7 g
Octanol	CH₃CH₂CH₂CH₂CH₂CH₂CH₂CH₂OH	0 g

Units of Concentration

We know already few units of concentration

Molarity (M)

M = mol_solute / 1 L_sol'n

Mole Fraction (Χ)

Χ = mol_solute / mol_total

Mass Percent (%_mass)

%_mass = g_solute / g_total x 100%

Parts per million (ppm) = g_solute / g_total x 10⁶

Parts per billion (ppb) = g_solute / g_total x 10⁹

Molality (m)

m = mol_solute / 1 kg_solvent

Density (d) can also be considered as concentration unit, in this respect.

Conversion between these units is accomplished, none other than, yes, Dimensional Analysis!

Example: Consider an aqueous solution of CO(NH₂)₂ with its d = 1.00 g/mL. Given that m = 2.577 m, what are the %_mass of solute, ppm of solute, mole fraction of solvent, and molarity?

μ_CO(NH₂)₂ = 60.062 g/mol

$? g_{C O {(N H_{2})}_{2}} = 2.577 m o l_{C O {(N H_{2})}_{2}} (\frac{60.062 g_{C O {(N H_{2})}_{2}}}{1 m o l_{C O {(N H_{2})}_{2}}}) = 154.779774 g$

Therefore, total mass, m_total= 1000 g + 154.779774 g = 1154.779774 g, then $% = (\frac{154.779774 g}{1154.779774 g}) 100 % = 13.40 %$

For ppm, instead of multiplying 100 to the ratio, 10⁶ is mulitiplied to obtain
1.340 x 10⁵ ppm.

For χ, you need the total number of moles, which is the sum of mol_solute + mol_solvent. The # of moles of solvent is,

$? m o l_{H_{2} O} = 1 k g_{H_{2} O} (\frac{10^{3} g_{H_{2} O}}{1 k g_{H_{2} O}}) (\frac{1 m o l_{H_{2} O}}{18.016 g_{H_{2} O}}) = 55.506 m o l$

Combining the two contributions, mol_total = 55.560 + 2.577 = 58.10832 mol, so χ_solvent is given by χ = 55.560 mol / 58.10832 mol = 0.9556.

For molarity, assuming the solution density is 1.00 g/mL, we can convert total mass of solution, which was calculated to be 1154.8 g = 1.1548 L in volume, thus to obtain M = 2.323 M.

Example: The density of an aqueous solution containing 10.0 % ethanol (C₂H₅OH) by mass, is 0.984 g/mL. Calculate the molality, molarity, and volume of the solution would contain 0.200 mole of ethanol?

There are 10.0g ethanol and 90.0g water in the solution. We should convert the mass of ethanol into moles. $?_{m o l_{e t h}} = 10.0 g_{e t h} (\frac{1 m o l_{e t h}}{46.07 g_{e t h}}) = 0.217 m o l$ We need also to convert the denominator for molality, which is 90.0 g to kg, that is 0.0900 kg. Therefore, $m = \frac{0.217 m o l}{0.0900 k g} = 2.41 m$ For molarity, the solution volume is obtained from 100 g of the solution. $?_{m L} = 100 g (\frac{1 m L}{0.984 g}) (\frac{1 L}{10^{3} m L}) = 0.102 L$ Therefore, $M = \frac{0.217 m o l}{0.102 L} = 2.13 M$ The last bit is asking for volume, thus we use molarity. $?_{m L} = 0.200 m o l (\frac{1000 m L}{2.13 m o l}) = 93.9 m L$

Factors affecting Solubility

Effect of Temperature

Generally, higher the temperature more solute can be dissolved.

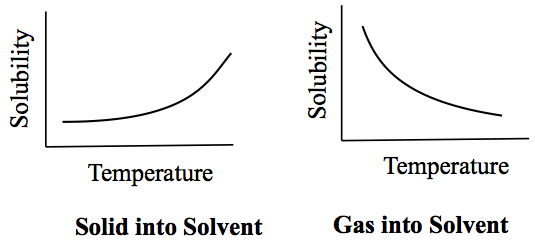
Solid dissolving in water generally increases, while gas in water decreases.

Except:
NaCl doesn't really change its solubility over the range of 0°C to 100°C. In addition, Ce₂(SO₄)₃ actually decrease its solubility in the range of 0°C to about 40°C.

Effect of Pressure

The concentration of gas is proportional to the gas pressure applied.

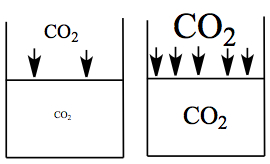
Therefore, we have

[ ] = k P_gas

where [ ] is the concentration of gas in solution, and k is called Henry's law constant with M/atm unit.

The constants differ for different gas molecules. For example, the Henry's law constant for O₂ is 1.3 X 10^-3 mol/Latm, while for N₂ is 6.8 X 10^-4 mol/Latm.

Example: Assuming that the partial pressure of oxygen and nitrogen in air to be 0.20 atm and 0.80 atm, respectively, calculate the mole fractions of oxygen and nitrogen in water at 298 K.

We should first know the concentration of the O₂ and N₂ that are dissolved in water by using the Henry's law. $c = k_{O_{2}} P_{O_{2}} = (1.3 \times 10^{-3} M / a t m) (0.2 a t m) = 2.6 \times 10^{-4} M$ Similarly for N₂, c = 5.44 X 10^-4 M. Assuming we have 1 L of solution, we have 2.6 X 10^-4 mol_O₂ and 5.44 X 10^-4 mol_N₂ in the solution. So, the solution is a three-component system now. It means that in order for us to calculate the mole fractions, we also nee to know the number of moles of the solvent. Assuming that the density of water is 1.00 g/mL, we have $? {m o l}_{H_{2} O} = 1000 g_{H_{2} O} (\frac{1 m o l}{18.016 g_{H_{2} O}}) = 55.506 {m o l}_{H_{2} O}$ Therefore, $n_{O_{2}} + n_{N_{2}} + n_{H_{2} O} = n_{t o t a l}$ The total number of moles is 55.5068 mol. Therefore, the mole fractions are: $χ = \frac{n_{O_{2}}}{n_{t o t a l}} = \frac{2.6 \times 10^{-4} m o l}{55.5068 m o l} = 4.7 \times 10^{-6}$ Similarly, χ_N₂ = 9.8 X 10^-6.

Colligative Properties

Physical changes induced by small amount of solute. They depend only on the concentration, and not the nature and/or type of solute.

4 types

Vapor pressure lowering - Raoult's Law

Boiling point elevation

Freezing point depression

Osmotic pressure

Raoult's Law: Vapor Pressure Lowering

In comparison to pure liquid, solution has lower vapor pressure. The vapor pressure depends on the mole fraction of solvent, χ₁.

For solvent with non-volatile solute

P_{1} = P_{1}^{\circ} χ_{1}

where subscripts 1 indicates that it is for solvent, and ° (the circle on P) indicates for the vapor pressure of pure solvent.

You can put the above equation in terms of change in pressure by introducing the solute into pure solvent in a following manner. Since there are only two component, χ is of two parts χ₁ for the solvent and χ₂ for the solute. Furthermore, χ₁ + χ₂ = 1. So, χ₁ = 1 - χ₂, and substitute this into P₁ = P^°₁ χ₁ yields $P_{1} = P_{1}^{\circ} (1 - χ_{2}) = P_{1}^{\circ} - P_{1}^{\circ} χ_{2}$ Therefore, $P_{1}^{\circ} - P_{1} = Δ P = P_{1}^{\circ} χ_{2}$

Example: How many grams of glucose, C₆O₆H₁₂ (μ=180.2 g/mol), is required to obtain the vapor pressure change of 1.4 mmHg in 460 mL of water at 30°C? The vapor pressure of pure water at 30°C is 31.82 mmHg. Assume density of water at this temperature is 1.00g/mL.

It means that we know ΔP to be 1.4 mmHg. Then, using the last equation, we can arrive at the mole fraction of glucose (χ₂).

$χ_{2} = \frac{Δ P}{P_{1}^{\circ}}$ Substituting the numbers in, yields: $χ_{2} = \frac{1.4 m m H g}{31.82 m m H g} = 0.044$ Since χ is a mole fraction, and we know the amount of water we can obtain the number of moles of glucose in the following way: $χ_{g l u c o s e} = \frac{n_{g l u c o s e}}{n_{t o t a l}} = \frac{n_{g l u c o s e}}{n_{g l u c o s e} + n_{w a t e r}}$ $n_{g l u c o s e} = \frac{n_{w a t e r} χ_{g l u c o s e}}{1 - χ_{g l u c o s e}}$ So, we need to know the number of moles of water, for which we have 460 mL. $? m o l_{w a t e r} = 460 m L_{w a t e r} (\frac{1 g}{1 m L}) (\frac{1 m o l}{180.2 g}) = 2.553 m o l$ Substitute this into the mole of glucose is, then: $n_{g l u c o s e} = \frac{(2.553 m o l) 0.044}{1 - 0.044} = 0.11749 m o l$ $? g_{g l u c o s e} = 0.11749 m o l_{g l u c o s e} (\frac{180.2 g}{1 m o l}) = 21.172 g = 21 g$

For solvent with volatile solute

The total pressure now contains, not only the solvent vapor, but also contains solute vapor. Therefore, the total pressure is a sum of the two contributions

P_total = P_solv + P_solute = P°_solv χ_solv + P°_solute + χ_solute

Boiling Point Elevation

Boiling point is higher in solution than that of pure solvent.

ΔT = k_b m

where ΔT is the change in boiling point, m is the molality of sol'n, and k_b is the boiling point elevation constant. For water as solvent, k_b is 0.516 °C kg/mol.

k_b = 0.516 °C kg/mol

For ionic solute, the equation must be corrected by van't Hoff factor, i

ΔT = i k_b m

The van't Hoff factor is close to the number of ions from a solute molecule, but it does depend on the extent of dissociation. Effectively it is the # of ions, for our purpose.

Example: Let's say that you are at camp site. You are asked to cook up some veggies. You have 500 mL of water in your pot (density = 1.00g/mL), and added 10.0 % by mass of salt, NaCl. At what temperature would the pot of salt water boil?

We can start with calculating the concentration in molality of NaCl. Since the mass of NaCl is 10% of water, we have 50.0g of NaCl. $? m o l_{N a C l} = 50.0 g_{N a C l} (\frac{1 m o l_{N a C l}}{58.4 g_{N a C l}}) = 0.8562 m o l_{N a C l}$ The molality of the NaCl solution is $m = \frac{0.8562 m o l_{N a C l}}{0.500 k g} = 1.712 m$ We apply the boiling point elevation expression $Δ T = i k_{b} m = 2 (0.516 ° C k g / m o l) 1.712 m o l / k g = 1.767 ° C$ Therefore, 1.8°C increase in temperature. So, the 10% solution of NaCl boils at 101.8°C.

Freezing Point Depression

For freezing point, the effect of having solution is in the opposite of boiling point, and the freezing point measured with sol'n is lower than the pure solvent.

ΔT = k_f m

where ΔT is the change in freezing point, m is the molality of sol'n, and k_f is the freezing point depression constant. For water as solvent, k_f is 1.86 °C kg/mol.

k_f = 1.86 °C kg/mol

For ionic solute, the equation must be corrected by van't Hoff factor, i

ΔT = i k_f m

Example: You are asked to design an antifreeze system of a radiator for automobile use. Let's say that the radiator has a capacity of 10.0 L, and ethylene glycol, C₂H₆O₂, is the mixed with water to make the antifreeze solution. Let's say that it is capable of withstanding the cold temperature of 14°F. How many kg of ethylene glycol does the radiator require to the temperature? Assume that density of water is 1.000 g/mL.

We first need to convert 14°F to Celcius scale. $T ({}^{\circ}F) = \frac{5}{9} [T ({}^{\circ}C) - 32]$ $T ({}^{\circ}C) = \frac{5}{9} (14 - 32) = - 10 {}^{\circ}C$ Therefore, the ΔT = 10°C. We use this in $Δ T = k_{f} m$ . We solve for m (molality) with k_f = 1.86 °C kg/mol. $m = \frac{Δ T}{k_{f}} = \frac{10 {}^{\circ}C}{1.86 {}^{\circ}C k g / m o l} = 5.376 m o l / k g$ Since the capacity of the radiator is 10.0L, therefore, the mass is 10.0 kg, so this can be converted to ethylene glycol mass. $? k g_{e t h y l e n e} = 10 k g_{w a t e r} (\frac{5.376 m o l_{e t h y l e n e}}{1 k g_{w a t e r}}) (\frac{62.07 g_{e t h y l e n e}}{1 m o l_{e t h y l e n e}}) (\frac{1 k g}{10^{3} g}) = 3.34 k g$

Consider also a question like the following:
Given the area of your yard and the height of snow on your yard, can you calculate the amount of salt (KCl) required to melt all snow, if outside temperature is 25°F and the density of the newly fallen snow is 0.15 g/cm³?

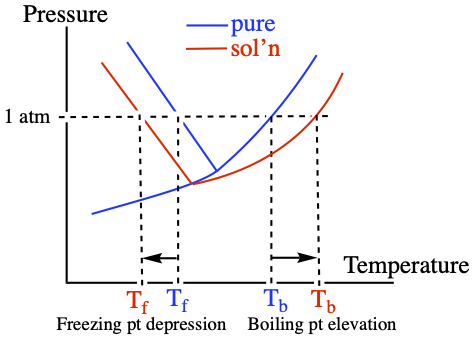
Pictorially, in terms of phase diagram, the freezing point depression and boiling point elevation are manifestation of the shift observed in the phase diagram, as shown below. The blue curve is the phase diagram for, say, pure water, and the red is for solution.

Osmotic Pressure

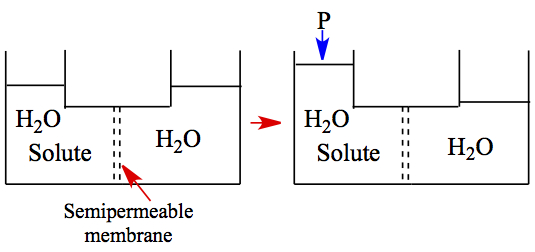A bent tube, with a semipermeable membrane where only H₂O molecules can pass, contains a solution on the left chamber and pure H₂O on the right. In order for the system to reach equilibrium to equalize the concentration, water moves from the right chamber to left. The pressure exerted on the left chamber to stop the flow of water from the right is called osmotic pressure, π. The relationship between π and concentration is as follows,

$π = \frac{n R T}{V} = M R T$ where M is the molarity of the solution. It resembles IGL!

Example: Often protein molar mass is obtained from osmotic pressure measurement. If a solution of protein is prepared by dissolving 0.0500 g of the protein in 10.00 mL water, measuring an osmotic pressure of 15.5 mm_Hg at 20.0°C, what is the molar mass of protein?

Rearrange the equation so that

M = Π/RT

Π = 0.01974 atm,

so, n = [(0.01974 atmi)(0.01 L)]/(0.08206 Latm/molK)(293.15 K) = 8.2046 x 10^-6 mol_protein

and μ = 0.0500 g/(8.2046 x 10^-6 mol) = 6094 g/mol

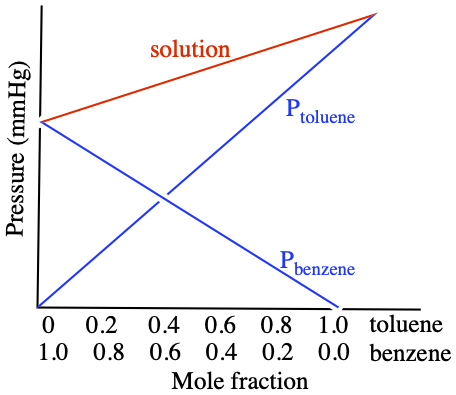
Fractional Distillation

From vapor pressure lowering for solutions with volatile solute,

$P_{t o t a l} = P_{1}^{\circ} χ_{1} + P_{2}^{\circ} χ_{2}$ where subscripts 1 and 2 indicate solvent and solute that consists the solution, respectively. If you plot above equation in terms of a solution made of benzene and toluene in different composition, you might see something like this.

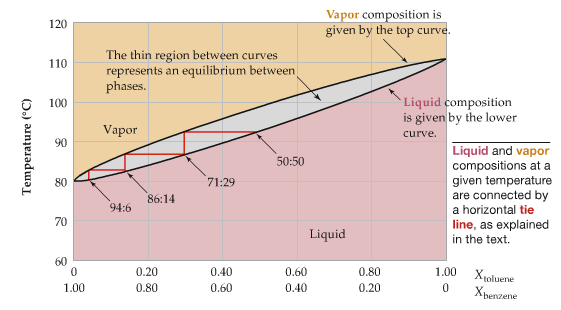
In this graph, the blue curves are for vapor pressures of pure substances, and the red curve is for the solution. The solution vapor pressure is calculated by the equation above. You can plot temperature as a function of mole fractioin, instead, and is shown below.

The diagrams shows the temperature phase diagram as a fxn of mole fraction.

The top part (orange shade) is gas phsae, and the bottom part (pink) is the liquid. The phase boundary in this diagram is separated, due to the volatile nature of the solute. It means that at a certain temperature, the vapor composition (mole fraction) is different from that of the liquid composition (mole fraction).

For example, at 90°C, vapor has 20% toluene, but liquid has 40% toluene. This difference is utilized to concentrate, for example, alcohol from a dilute solution.

Example: Let's say that you are distilling a solution of alcohol with the mole fraction of alcohol to be 0.05. Your distiller operates at 64°C, at which vapor pressure of water is 153 mm_Hg, and of ethanol is 400 mm_Hg How many iterations does it take to alchohol content to be higher than 50%_mole alchohol?

So, we start with:
χ_alc = 0.05 : P°_alc = 400 mm_Hg
χ_water = 0.95 : P°_water = 153 mm_Hg

Since P = P° χ, vapor pressures are

P_alc = (400 mm_Hg)(0.05) = 20 mm_Hg
P_water = (153 mm_Hg)(0.95) = 145.35 mm_Hg

Then, P_total = 165.35 mm_Hg So, now we can recompute the mole fraction in vapor by using χ = P/P_total

We have:

χ_alc = 20 mm_Hg/165.35 mm_Hg = 0.121
χ_water = 145.35 mm_Hg/165.35 mm_Hg = 0.879

Now, you see alcohol content went up more than twice as much! If you condense this vapor to a liquid, and do the calculations over, you get:

2^nd iteration
P_alc = (400 mm_Hg)(0.121) = 48.4 mm_Hg
P_water = (153 mm_Hg)(0.879) = 134.5 mm_Hg

P_total = 182.9 mm_Hg

χ_alc = 48.4 mm_Hg/182.9 mm_Hg = 0.265
χ_water = 134.5 mm_Hg/182.9 mm_Hg = 0.735

3^rd iteration
P_alc = (400 mm_Hg)(0.265) = 106.0 mm_Hg
P_water = (153 mm_Hg)(0.735) = 112.4 mm_Hg

P_total = 218.4 mm_Hg

χ_alc = 106.0 mm_Hg/218.4 mm_Hg = 0.485
χ_water = 112.4 mm_Hg/218.4 mm_Hg = 0.515

4^th iteration
P_alc = (400 mm_Hg)(0.485) = 194.0 mm_Hg
P_water = (153 mm_Hg)(0.515) = 78.8 mm_Hg

P_total = 272.8 mm_Hg

χ_alc = 194.0 mm_Hg/272.8 mm_Hg = 0.711
χ_water = 78.8 mm_Hg/272.8 mm_Hg = 0.289

So, after 4 iterations, alcohol content is over 70%.

In actual experiment, the iterations are done naturally by setting up an apparatus such as shown below. You're going to use this set-up in Organic Chemistr next year!

By Original PNG by User:Quantockgoblin, SVG adaptation by User:Slashme - http://en.wikipedia.org/wiki/distillation, Public Domain, Link

Colloids

Colloid = dispersion of particles in another medium. There are several shown below:

dispersing medium	dispersed phase	name	example
gas	liquid	aerosol	fog
gas	solid	aerosol	smoke
liquid	gas	foam	whipped cream
liquid	liquid	emulsion	mayonnaise
liquid	solid	sol	milk of magnesia
solid	gas	foam	plastic foam
solid	liquid	gel	butter, jelly
solid	solid	solid sol	alloy

Tyndall effect: Light scattering in colloids. Color that is scattered depends on the size of the suspended particles. --- important tool in pharmaceutical research, called dynamic light scattering. The following shows that the white light has been scattered in the colloidal suspension.

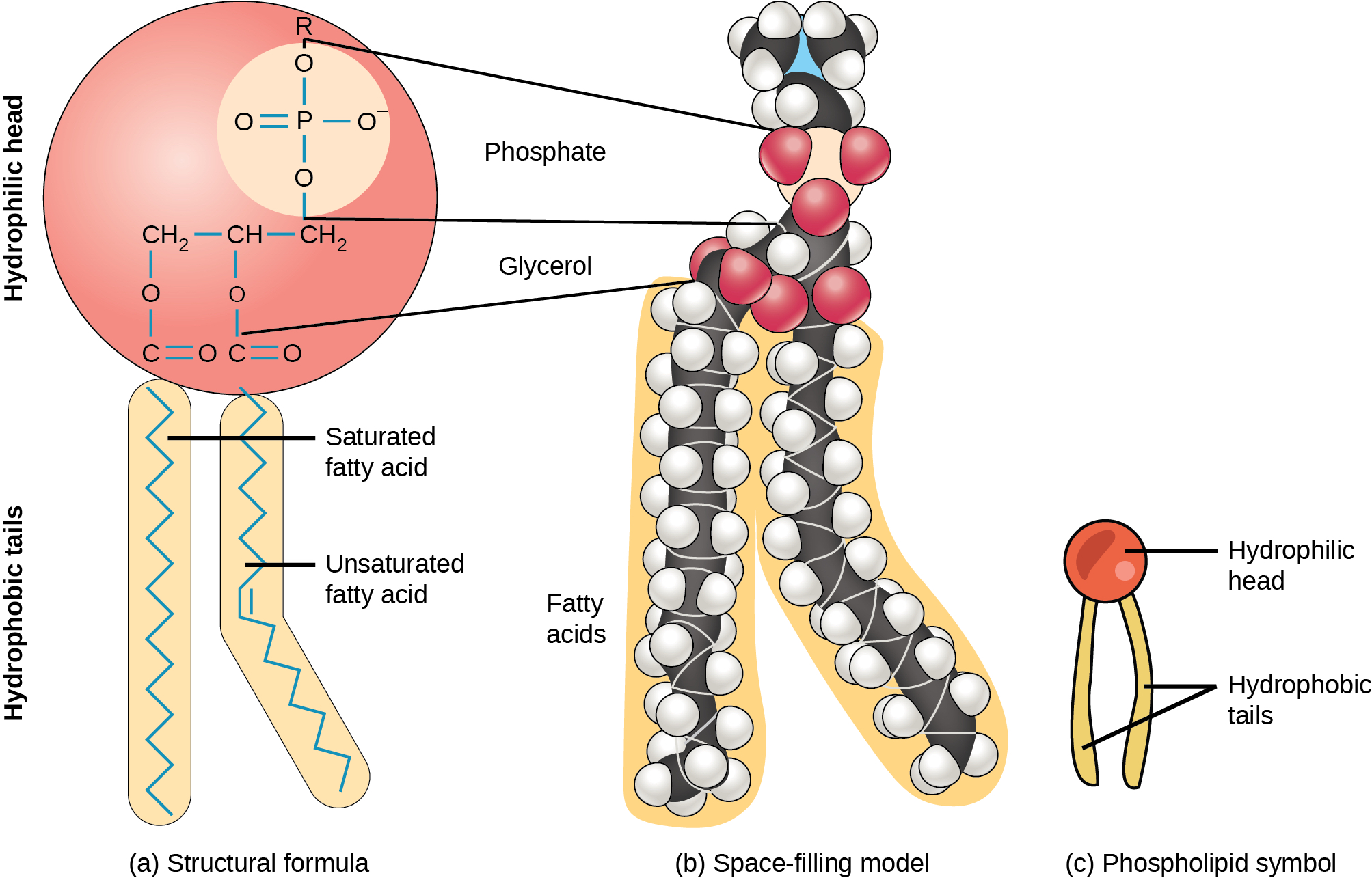
Hydrophilic and Hydrophobic Colloids

Two categories of colloids: 1) Hydrophilic and 2) Hydrophobic Example of hydrophilic colloids is protein in water. Hydrophobic colloids is not stable. For example, oil is not easily suspended in water.

However, amphiphilic molecules can suspend large hydrophobic molecules in water. Amphiphiles are the molecules that possess both hydrophilicity and hydrophobicity within it. Biological cell is composed of phospholipids as you might know, as shown below. The assembly of such molecules make a cell membrane.

Assembly of the phospholipids makes up cell membrane, which you might have seen in the biology class.

The picture above is from Wiki on cell membrane.