General Properties of Aqueous Solns
Solution (sol'n) = two component system.
Aqueous Chemical Rxns we study in this chapter
We'll examine three types of chemical reactions in aqueous solution.
- 1) Precipitation rxns
- 2) Acid-Base rxns
- 3) Reduction-Oxidation rxns
Electrolytes
Electrolyte — solutions of ion- Conducts electricity — hence the name
- When the compounds is dissolved in an aqueous environment,
the molecules dissociate into two ions, cation and
anion.
- Strong electrolyte — complete dissociation occurs
- Examples include: HCl, HNO3, NaCl, NaOH, KOH, Ba(OH)2
- Weak electrolyte — incomplete dissociation (usually less than
10%)
- Examples include: HF, CH3CO2H
- Nonelectrolyte — no dissociation occurs
- Examples: H2O, glucose(C6H12O6)

In the figure above, the solution in the beaker is incorporated as a part of electrical circuit. The solutions in the beaker are: (a) nonelectrolyte, (b) weak electrolyte, and (c) strong electrolyte
Precipitation Rxns and Solubility
When NaCl is mixed with AgNO3 in water, you might write chemical equation as,
The chemical eqn above may be described as molecular equation, where all species are accounted for. However, ionic compound such as NaCl ionizes
- When NaCl(s) is placed in water →
Na+(aq) + Cl-(aq)
- Similarly, if we dissolve AgNO3(s) in water
→
Ag+(aq) + NO3-(aq)
Further, if we add NaCl(s) and AgNO3(s) into water, it makes sense that → Na+(aq) + Cl-(aq) + Ag+(aq) + NO3-(aq)
Let's say that Ag+ and Cl- ions react to form AgCl(s ), and no other ions react. Then, the reaction is written as,
Na+(aq) + Cl-(aq) + Ag+(aq) + NO3-(aq) → Na+(aq) + AgCl(s) + NO3-(aq)
Since Na+ and NO3- ions don't react, they appear on the both sides of the equation. Chemical equation is similar to mathematical equation, if the same species appears on the both sides of the equation, they cancel each other. Thus, we have,
Ag+(aq) + Cl-(aq) → AgCl(s)
This type of equation, after cancellation, is called net ionic equation.
| molecular eqn | NaCl + AgNO3 → AgCl(s) + NaNO3 |
| ionic eqn | Na+(aq) + Cl-(aq) + Ag+(aq) + NO3-(aq) → Na+(aq) + AgCl(s) + NO3-(aq) |
| net ionic eqn | Ag+(aq) + Cl-(aq) → AgCl(s) |
Precipitate (PPT) — solid formed in solution as a result of chemical rxn
PPT rxn — rxn produces PPT
Another way to think about PPT rxn is that two soluble molecules dissolved in water in the form of cations and anions, are recombined such that the new molecule is no longer soluble in water, and becomes insoluble, thus precipitate out.
Why? Simply put: The process is energetically favored. (Much more on this in Chapter 8!)
How can we tell what combinations of ions would form PPT in aqueous solution? The following table shows solubility of cation—anion combination.
| NO3- | X- | ClO4- | CH3CO2- | SO42- | OH- | CO32- | PO43- | |
|---|---|---|---|---|---|---|---|---|
| Gr 1 cations NH4+ | sol | sol | sol | sol | sol | sol | sol | sol |
| Gr 2 cations | sol | sol | sol | sol | BaSO4 | Mg(OH)2 | insol | insol |
| TM | sol |
AgX Hg2X2 PbX2 |
Ba(ClO4)2 Hg2(ClO4)2 Pb(ClO4)2 |
Ba(CH3CO2)2 Hg2(CH3CO2)2 Pb(CH3CO2)2 |
sol | insol | insol | insol |
| Gr = group on P.T. X = halogens (Cl, Br, I), sol = soluble, insol = insoluble. Compounds written in red are specific compounds that are insoluble, otherwise the combination is soluble in general. |
Example: Write molecular, ionic and net ionic equations for adding the following compounds in water: a) HCl and AgNO3 b) K3PO3 and CaNO3 c) AgI and NH4ClO4
Example: Write net ionic equations for the following,
H2SO4(aq) + MgCO3(s) → H2O(l) + CO2(g) + MgSO4(aq)
Hg2(NO3)2(aq) + 2NH4Cl(aq) → Hg2Cl2(s) + 2NH4NO3(aq)
Acids, Bases, and Neutralization Rxns
As seen in Chapter 3,
Acid produces H+
Base produces OH-
Acid + Base → H2O — Neutralization rxn
If you write down molecular equation for acid and base reaction, you would get:
Strong Acid—Complete dissociation into H+ and anion
- example: HCl → H+ + Cl-
Strong Base—Complete dissociation into cation and OH-
- example: NaOH → Na+ + OH-
Weak Acid—Incomplete dissociation into H+ and anion
- example: HC2H3O2 ⇄ H+
+ C2H3O2-
⇄ indicates that all three species are present in the solution (said to be in equilibrium)
Weak Base—Incomplete dissociation into cation and OH-
- example: NH3 + H2O ⇄ NH4+
+ OH-
Neutralization Rxns
Three circumstances:
1) Strong acid reacting with strong base
- H+ + OH- → H2O
2) Weak acid (HA) reacting with strong base
- HA ⇄ H+ + A-
- H+ + OH- → H2O
- Combining the two yields
- HA + OH- → A- +
H2O
3) Strong acid (HA) reacting with weak base (B)
- B + H2O → BH+ +
OH-
- H+ + OH- → H2O
- Combining the two, yields
- B + H+ → BH+
The following lists the common acids and bases that you encounter in this course.
Common Acids and Bases with their strength
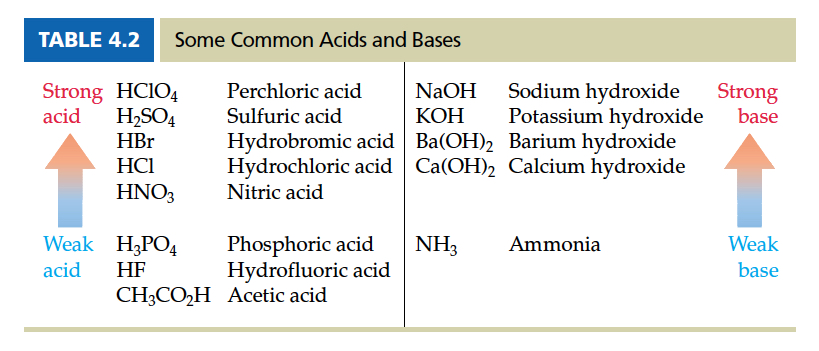
Example: Write net ionic equation for adding Sr(OH)2 and HF in aqueous environment.
Since Sr(OH)2 is a strong base, and HF is a week acid, we have:
HF ⇄ H+ +
F-
H+ + OH- → H2O
HF + OH- → H2O +
F-
Example: Write net ionic equation for adding Ba(OH)2(aq) and CH3CO2H(aq).
Acetic acid CH3CO2H is a weak acid, thus,
H+ + OH- → H2O
CH3CO2H + OH- → H2O + CH3CO2-
Example: Write net ionic equation for adding NH3(aq) and HCl(aq).
Ammonia NH3 is a weak base, thus,
H+ + OH- → H2O
NH3 + H+ → NH4+ + OH-
Example: 4.33(b) Balance the following equation and write the ionic and net ionic equation. Ba(OH)2(aq) + H3PO4(aq) →
Ba(OH)2 is strong base, H3PO4 is weak acid. Thus,
H+ + OH- → H2O
For net ionic equation we add these two equations, nad we get
Reduction—Oxidation Rxns (Redox rxns)
Electron transfer between two different species
- One loses an electron — Oxidation
- One gains an electron — Reduction
So,
Zn2+ 2e- → Zn reduction
This eqn can be interpretted to have neutral Cu giving 2 electrons to Zn2+, therefore, Cu becomes Cu2+ and Zn2+ becomes Zn. Another words, oxidation and reduction ocurr simultaneously.
Many biological catalysts are Redox in nature:
- Fe in hemoglobin
- Co in vitamin B12
- Cu in cytochrome
- Mo in nitrogenase
The following shows how to balance red-ox equation. Yes, it is tedius!
| Steps involved in balancing the redox eqn. |
|
| If the solution is basic, add enough OH- on the both sides of the equation so that all H+ becomes H2O |
Oxidation number, ox#
Ox# is a fictitious charge of atoms in molecule. We can easily assign the ox# for each atom in a molecule by using the following priority table. Priority becomes lower as you go down the list.
| Priority | Atom types | Assigned Ox# | Examples |
|---|---|---|---|
| 1 | Atoms in their element state | 0 | Br2 Br is 0 |
| 2 | Monatomic ion | charge | Cl-, Ox# = -1 |
| 3 | Total of ox# in a molecule in an ion | sum = 0 sum = charge | |
| 4 | In their compounds, Gr IA Gr IIA | +1 | KCl,
ox#K=+1 MgCl2, ox#Mg=+2 |
| 5 | F in compounds | -1 | CH2F2, ox#F=-1 |
| 6 | H in compounds | +1 | H2O each H, ox#=+1 |
| 7 | O in compounds | -2 | H2O each O, ox#=-2 |
| 8 | In their compounds, Gr 17A Gr 16A Gr 15A | -1 -2 -3 | HCl, ox#Cl
= -1 H2Se, ox#Se = -2 PH3, ox#P = -3 |
Example: What are the oxidation numbers for N and O in NO3-?
N is a Group 15A element. So, oxygen has higher priority than N. It means that we assign O to have ox#=-2. Then, let's call ox# for N as x. Using the this fact as well as the item #3 where the total of the ox#'s in an ion is ionic charge, we can set up the following,
Sovling for x, giving x = +5. Therefore, ox#N = +5.
Calculate the ox# for the following.
H2S, CH4, SF4, CO2, FeO42-
When ox# in the rxn becomes smaller, it is reduction.
When ox# in the rxn becomes larger, it is oxidation.
I'll give you the balanced red-ox equation for this section. However, you are responsible for which species is reduced or oxidized according to the oxidation number (ox#) and are responsible to deduce the unbalanced half-reactions.
Balancing Half-Rxns
The 4 steps to balance half-rxn:
- a) Balance all atoms other than H and O
- b) Balance O by adding H2O
- c) Balance H by adding H+
- d) Balance charge by adding H+
Combining the two Half-Rxns
To combine the balanced half-rxns, we need to cancel out all the free electrons, denoted as e-.
Example: Balance the following rxn:
First, we need to assign ox# so that we know which compound is oxidized or reduced. Using the priority table, we assign ox# as,
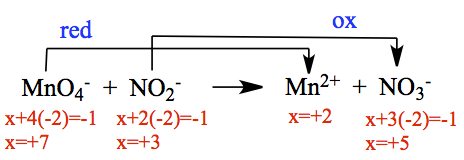
As you can see, the ox# on Mn in the reactant is +7, and that became +2 in the product side (ox# is reduced in magnitude, hence 'reductions'), therefore the process is reduction. N was the unknown ox# for NO2- and NO3-, and the magnitude of ox# had increased, which is oxidation process.
Now we can divide the above equation into two half-rxns as,
ox NO2- → NO3-
Let's balance each of these now. First, we need to balance atoms other than H and O. In the reduction case, it is Mn, and in the oxidation case, it is N. In the reduction, there is only one Mn on the both sides of the equation, therefore, they are balanced. In the oxidation the same is true; N are balanced.
The next step is to balance O by adding H2O. Then,
ox NO2- + H2O → NO3-
In the reduction, there are 4 O's of the left-hand side of the equation, therefore 4H2O were added. Similarly for oxidation one H2O on the left-hand side was needed.
We need to balance H by adding H+. In the reduction side, we added 4 H2O, therefore, we have 8 H altogether. So, we add 8H+ on the left-hand side. In the oxidation, we need to add 2H+ on the right-hand side. Then, we have
ox NO2- + H2O → NO3- + 2H+
The last step is to balance the charge by adding e-. In the reduction, the total of the charge is +7 on the left-hand side (-1 from MnO4- and +8 from H+), and +2 on the right-hand side. So, if 5e- is added to the left-hand side, the total charge becomes +2, which is the same as on the right-hand side. Similarly, in the oxidation, if 2e- is added to the right-hand side, both sides become -1 charge.
ox NO2- + H2O → NO3- + 2H+ + 2e-
We now need to combine the two half-rxns to make into an overall equation. You notice in the two half-rxns that electrons appear on the opposite sides of the equations. When combined, and if the same number of electrons appear they cancel over and across the arrow of the chemical equation. Currently, we have 5e- on the left and 2e- on the right. So, if we multiply the entire reduction equation by 2 and multiply the entire oxidation equation by 5, we find 10 electrons in each of the equations. That is,
ox 5( NO2- + H2O → NO3- + 2H+ + 2e-)
By distributing the factors by combining the two half-rxns, we get
Finally, we arrive at,
| 2MnO4- + 6H+ + 5NO2- → 2Mn2+ + 3H2O + 5NO3- |
This is the balanced red-ox equation.
As seen above, there are 6H+ in this equation. This implies that the reaction is in acidic condition. If in case, you desire to carry out the reaction in basic condition, you must add 6OH- to the both sides of the equation. Therefore,
Then, some of the water cancel out, and leads to the balanced red-ox equation in basic condition is,
| 2MnO4- + 3H2O + 5NO2- → 2Mn2+ + 5NO3- + 6OH- |
Example: Blood alcohol level can be determined by a titration with potassium dichromate according to the following (not balanced):
What is the blood alcohol level in mass percent if 8.76 mL of 0.04988 M K2Cr2O7 is required for titration of a 10.002 g sample of blood?
We first need to balance the equation above. We need to determine what's been reduced or oxidized. Let's assign ox#.
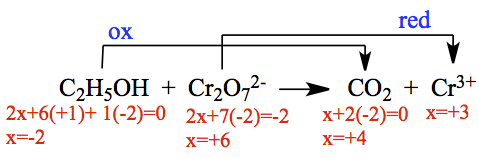
It means,
ox C2H5OH → CO2
Balance atoms other than O and H.
ox C2H5OH → 2CO2
Balance O by adding H2O.
ox C2H5OH + 3H2O → 2CO2
Balance H by adding H+.
ox C2H5OH + 3H2O → 2CO2 + 12H+
Balance the charge.
ox C2H5OH + 3H2O → 2CO2 + 12H+ + 12e-
Combining by multiply the reduction equation by 2, and add together,
Now we can do the dimensional analysis. We need to know the mass of C2H5OH in the sample. We start our calculation by using the given as 8.76 mLK2Cr2O7.
Therefore, we have
Molarity, unit of concentration
Solution
A solution is a two component system where the smaller component is called solute and the larger component is called solvent.
Concentration is a measure of amount of solute in the solution. The most common concentration unit is Molarity, M.
By knowing the concentration of the solution, you can predict the theoretical yield of products, and others. Molarity contains two units, molsolute and Lsolution. So, molarity can be used as a conversion factor in the dimensional analysis!
Example: Molarity #1
You have a 30 mL solution of 1.0 M NaCl. How many moles of NaCl are in the solution?
Example: Molarity #2
You have a 1.0 M solution of NaCl. How many mL are there if the solution contains 0.02 mol of NaCl?
Example: Molarity #3
You have 50.00 mL solutioin of 3.50x10-2M NaOH. How many mol of OH- ion are there?
Example: Molarity #4
You have 50.00 mL solutioin of 2.0x10-2M NaOH. How many g of OH- ion are there in the solution?
Molarity can be used in conjunction with the chemical equation to deduce, for example, how much product produced, how much reactant is needed, etc. Let us look at few.
Example: Molarity #5
Given the following reaction,
Example: Molarity #6
Given the following reaction,
Dilution
Often you encounter a situation that you need to make a solution from the concentrated solution. What do you do?
Dilution can be easily dealt with using dimensional analysis. Two example should illustrate the importance of using dimensional analysis.
Example: Dilution #1
How many mL of 0.500 M HCl do you need to make a 200.0 mL of 3.00 x 10-2 M HCl?
Example: Dilution #2
How many mL of 0.500 M Ba(OH)2 do you need to make a 200.0 mL of 3.00 x 10-2 M OH- solution?
Do you see the difference between the two examples above? So, how do you actually make the solution? Here is how.

More difficult question is:
Example: Dilution #3
What volume of 0.416 M Mg(NO3)2 should be added to 255 mL of 0.102 M KNO3 to produce a solution with a concentration of 0.278 M NO3- ions? Assume volumes are additive.
The situation is described as shown in the following diagram.
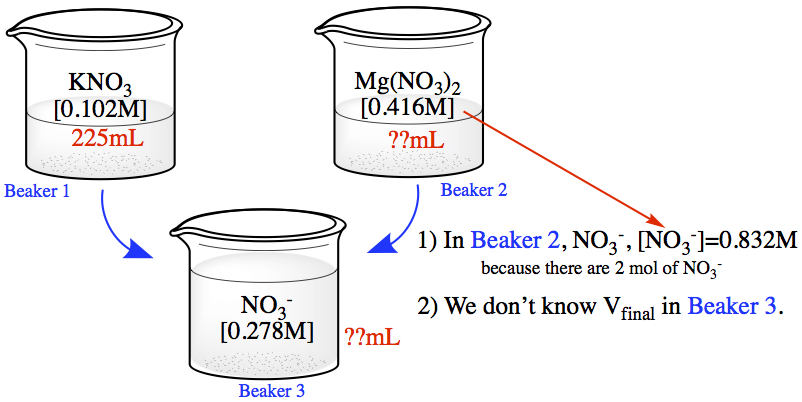
The first thing you must notice is that in Beaker 2 the concentration of NO3- = 0.832M, as a consequence of the chemical formula. Since we don't know the final volume of the solution in Beaker 3, we have to think a little.
In order to obtain the concentration specified in Beaker 3, we add contributions from Beakers 1 and 2, of course, which means:
| 1 |
| 2 |
| 3 |
| 4 |
Derivation of the equation above is shown below, if you care to know.
Substitute the numbers in, keeping in mind that the concentration, [NO3-]=0.832M.
Gravimetric Analysis
Gravimetric Analysis — Quantitative analysis based on measurement mass of compounds.In the ppt rxn section, we discussed adding AgNO3 solution to NaCl solution.
We came up with its net ionic equation to be,
Let's use the example above to solve a problem.
Example: How many grams of Cl is in the sample if 25.00 mL of 0.1975 M AgNO3 is required to convert all Cl to AgCl?
Example: A 40.00 mL of 0.0348 M Pb(NO3)2 is mixed with 0.00940 M aluminum iodide. a) Write net ionic equation. b) What is the minimum volume of AlI3 needed to complete the reaction? c) How many g of precipitate (product) form?
a)
b)
c)
Acid-Base Titration

Titration is a procedure to analyze the concentration of unknown quantity of some substance using known concentration of the other substance. These two different substances are related by chemical reaction. It means that you must know the balanced chemical equation to find out unknown.
The solution of known concentration is called standard solution, is placed in a buret. Slowly the standard solution is added to the solution containing unknown amount in a flask. When the stoichiometric amount of the standard solution is added, called the equivalence point, the reaction is complete and the titration is finished. In many reactions, the equivalence point is hard to detect, therefore one may add an indicator to the unknown to change color of the solution when some condition is met. Design of indicator that matches the equivalence point becomes, then, important.
Example: Acid-Base Titration #1
If a 50.0 mL of 0.50 M HCl is titrated with 0.20 M NaOH, how many mL of NaOH solution is needed to reach equivalence point?
The net ionic equation for this acid-base reaction is:

Example: Acid-Base Titration #2
If a 50.0 mL of 0.0224 M Ba(OH)2 is titrated with 1.72 x 10-2 M HF, how many mL of HF is required to reach equivalence point? Write a net ionic equation, first.
HF is a weak acid and Ba(OH)2 is a strong base. Therefore, the net ionic equation is:
Red-Ox Titration
Example: Red-Ox Titration #1
Bleach is a solution of sodium hypochlorite (NaClO). To determine the hypochlorite ion (ClO-) content, sulfide ion is added in basic solution and producing S(s) and aqueous chloride ion. Subsequently, the chloride ion is precipitated with AgNO3 to produce AgCl(s). When 50.0 mL of bleach (d = 1.02 g/mL) is treated as described above, 4.95 g of AgCl is obtained. What is the mass percent of NaClO in the bleach. First write two net ionic equations.
But the first one is red-ox equation because S2- → S is an oxidation process since the former has ox# = -2 and the latter ox# = 0. Then, you need to do what you need to do!
but the question stated that it is in basic solution, therefore add 2OH- to get rid of H+. Then,
From 4.95 g of AgCl, we can calculate the amount of NaClO since we have the balanced chemical equations. but, first convert 50 mL to g Then,