Chapter 5 Gases

Substances That Exist as Gases

Gas Pressure

Pressure is created by collisions of molecules to the wall

Higher the pressure → more collisions b/w molecules/area/time

Pressure is

P = \frac{F}{A} = \frac{m a}{A} = \frac{m g}{A} = ρ g h

with F = force, A = area, m = mass, g = gravity, and d = density. In deriving the expression, we used F = ma and m/A = dh.

Unit of pressure = Pascal (abriviated with Pa) = 1 kgm/s²
Barometric pressure = A column with 1 m x 1 m area and a height extending to the stragosphere containing air exerts 101325 Pa.

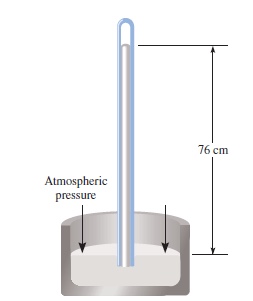
Mercury Column Barometer

Torrichelli (1643) used a column of mercury
At sea level height of columen measured = 760 mm_Hg
Define 760 mm_Hg = one standard atmosphere or 1 atm

Gravity (g = 9.800665 m/s²) pulls down mercury ⇄ air pressure pushes mercury (d = 13.595 g/cm³) up

Example: A barometer is filled with percholorethylene (d_per = 1.62 g/cm³). The liquid height is found to be 6.38 m. What is the barometric pressure in mm_Hg?

Since P_Hg = P_per, and expand each P with P = dgh (make sure to label each with subscripts!)

g d_Hgh_Hg= g d_perh_per
d_Hgh_Hg = d_perh_per
h_Hg = d_perh_per/d_Hg
h_Hg = 1.62 g/cm³6.38 m/13.595 g/cm³
h_Hg = 0.760 m = 760 mm = 1.00 atm

Manometer

Manometer = device to measure gas (well, just a flast with bent tube attached as shown)

If the gas inside the flask exerts the same pressure (P_gas) as atmosheric pressure (P_atm), the level of liquid in the tube must be leveled. Let's call it, Δh = 0.

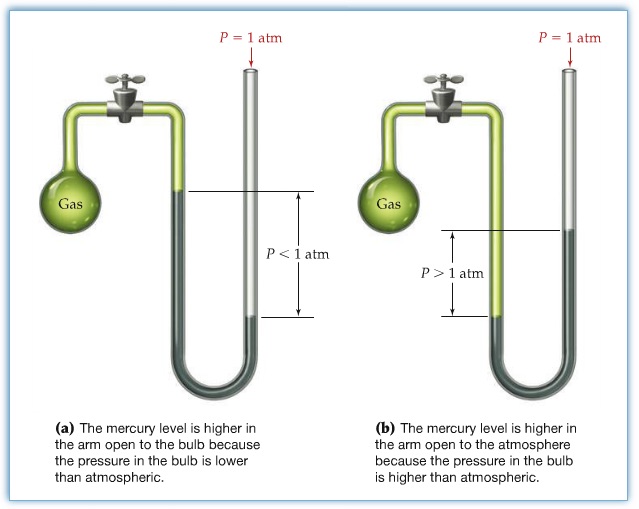
As seen on the graph left

If P_gas < P_atm → Δh < 0

This is the case for (a)

If P_gas > P_atm → Δh > 0

This is the case for (b)

Ideal Gas Law (IGL)

4 gas laws combined. 1) Boyle's Law, 2) Charles' Law, Gay-Lussac's Law and 4) Avogadro's Law

Boyle's Law (1662)
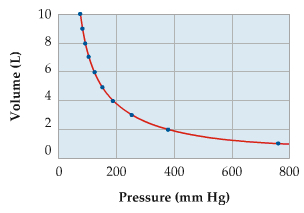
Relationship b/w P and V
Pressure is inversely proportional to Volume

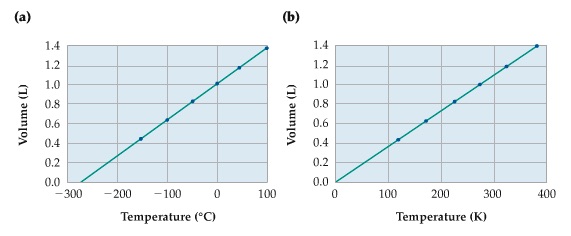
\begin{array}{l} P \propto \frac{1}{V} \\ P = \frac{c}{V} \end{array}

Charles' Law (mid 1800's)

Relationship b/w Volume and Temperature
Volume is directly proportional to Temperature.

\begin{array}{l} V \propto T \\ V = c T \end{array}

When the volume is plotted against temperature in the centigrade scale (a) in the graph, the temperature at which volume becomes 0, is the absolute 0 temperature. So, in (b) we rescale the temperature scale, called absolute temperature scale (the unit is called Kelvin, K).

Gay-Lussac's Law (1800-1802) (aka Amontons' Law): Relationship b/w Pressure and Temperature with constant volume.
Pressure is directly proportional to Temperature.

\begin{array}{l} P \propto T \\ P = c T \end{array}

Avogadro's Law (1811) Relationship b/w Volume and quantity of gas molecules (moles).
Volume is directly proportional to a number of moles.

$\begin{array}{l} V \propto n \\ V = c n \end{array}$

At the certain Temperature and Pressure

2H₂	+	O₂	→	2H₂O
2 mol		1 mol		2 mol
↓		↓		↓
2 L		1 L		2 L

Ideal Gas Law
Combining the four laws P = c/V or PV = c
P = cT
V = cT
V = cn
then
PV = ncT, and let us call c as R to obtain

PV = nRT

with R = 0.08206 Latm/(mol K).

Ideal Gas Equation

Let's use the IGL eqn to do some calculations!

Standard Temperature and Pressure (STP)

T = 0 °C = 273.15 K; P = 760 mm_Hg = 1 atm

P V = n R T

Solve for V and substitute the numbers in,

V = \frac{n R T}{P} = \frac{(1 m o l) (0.08206 L a t m / m o l K) (273.15 K)}{1 a t m} = 22.4 L

When the volume of one mole of gas is measured, Molar Volume @STP = 22.4 L.

Initial-Final State Problem

Since R is a constant, the ratio of PV and nT is also constant.

$R = \frac{P V}{n T}$

If we have a gas in a container (initial state, labeled with subscript i), we can modify the condition to the gas (final state, labeled with subscript f). These two states are related by R as

$R = \frac{P_{i} V_{i}}{n_{i} T_{i}} = \frac{P_{f} V_{f}}{n_{f} T_{f}}$

Example: 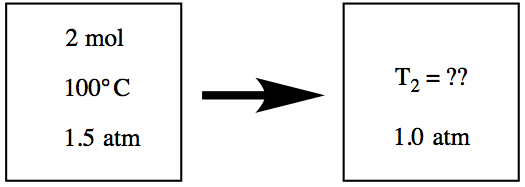We have a vessel containing 2 mol of gas at 100°C and at 1.5 atm,as seen in the picture.

If the pressure of the vessel is reduced to 1.00 atm, what is the temperature of the gas?

Since we didn't change the vessel during the experiment, the volume should be the same, and since we didn't open the vessel, number of gas molecules are the same before and after. It means that

$\frac{P_{i}}{T_{i}} = \frac{P_{f}}{T_{f}}$

$T_{f} = \frac{P_{f} T_{i}}{P_{i}} = \frac{(1.00 a t m) (373 K)}{1.5 a t m} = 248.67 K = - 24.5 ° C$

Molar Mass

The molar mass, μ with m and n are mass and # of moles, respecitvely, and its rearrangement is,

\begin{array}{l} μ = \frac{m}{n} \\ n = \frac{m}{μ} \end{array}

Substituting above into IGL $\begin{array}{l} P V = \frac{m R T}{μ} \\ μ = \frac{m R T}{P V} \end{array}$

Example: A glass vessel weighs 40.1305 g when clean, dry and evacuated. It weighs 138.2410 g when filled with H₂O at 25.0°C (ρ = 0.997 g/mL) and weighs 40.2959 g when filled with propylene gas at 740.3 mm_Hg at 24.0°C. What is the molar mass of propylene?

For propylene gas, we know P and T, so in the above equation for molar mass, we need to obtain m and V.

The mass of the gas is the difference b/w the mass of gass-filled vessel and of the empty vessel, i.e. m_gas = m_gas+empty - m_empty.

The volume of the gas, which equals the volume of the vessel, is obtained by knowing the mass of water in the vessel. The mass of water is converted to volume by its density given.

m_H2O = m_H2O+empty - m_empty
V_H2O = m_H2O[ 1 mL / 0.997 g ]

Then, substitue these into the expression for molar mass, as
$μ = \frac{(0.1654 g) (0.08206 L a t m / m o l K) (297.15 K)}{(0.9741 a t m) (0.09841 L)}$

μ = 42.08 g/mol

Gas Density

Rearranging the molar mass equation above, recognizing that m/V is density, ρ, therefore,

$ρ = \frac{m}{V} = \frac{P μ}{R T}$

Density of air depends on Temperature:

@ 0°C ρ = 1.2922 kg/m³
@15°C ρ = 1.2250 kg/m³
@20°C ρ = 1.2041 kg/m³
@30°C ρ = 1.1164 kg/m³

Example: At what temperature the density of O₂ be 1.00 g/L if the pressure is kept at 745 mm_Hg?

Solve for T in the density equation.

Then, T = (μ P)/(R ρ) = 382.26 K or 109°C

Example: 5.148. Estimate the distance in nm between molecules of water vapor at 100°C and 1.0 atm. Assume ideal behavior. Calulate first the number density of water, then you can think about the density in one dimension.

Add picture here!

The density of gas can be calculated from the equation above, i.e. $d = \frac{P μ}{R T}$ $d = \frac{(1.0 a t m) (18.02 g / m o l)}{(0.08206 a t m L / m o l T) (373.15 K)} = 0.5885 g / L = 0.5885 ✕ 10^{-3} g / {cm}^{3}$ Using the density, we can calculate how many water molecules are in the volume (1 cm³). $?_{water} = 1 {cm}^{3} (\frac{0.5885 ✕ 10^{-3} g}{1 {cm}^{3}}) (\frac{1 mol H_{2} O}{18.016 g_{H_{2} O}}) (\frac{6.022 ✕ 10^{23} H_{2} O}{1 mol H_{2} O}) = 1.9671 ✕ 10^{19} H_{2} O$ So, this value of 2 X 10¹⁹ water molecules are in three dimension. You can take the cube root of it to obtain the number of water molecules available in 1-dimension. ${(1.9671 ✕ 10^{19})}^{1 / 3} = 2.69945 ✕ 10^{6} H_{2} O$ So, we use this value in 1 cm as conversion factor and ask how many nm are there in 1 H₂O molecule. $?_{nm} = 1_{H_{2} O} (\frac{1 cm}{2.69945 ✕ 10^{6} H_{2} O}) (\frac{1 m}{100 cm}) (\frac{10^{9} nm}{1 m}) = 3.704 nm$ So, between molecules there are about 3.7 nm. According to the Internet source, the diameter of one water molecule is about 0.275 nm. So, at least about 10 times the size of the molecule is the neighboring water.

Gase Stoichiometry

Relating the amount of gas of reactant or product to other species in the reaction by stoichiometry. Notabean: PV = nRT only applies to gas species in the reaction!!

Example: What is the mass of Na(l), in grams, is produced, when 8.00 L of N₂(g) at 25.00°C and at 751 mm_Hg generated in the decomposition of sodium azide (NaN₃(s))?

2 NaN₃(s) → 2Na(l) + 3N₂(g)

?mol(N₂) = PV/RT = [(0.998158 atm)(8.00L)]/[(0.08206 Latm/molK)(298.15K)] = 0.3263795599 mol_N2

? g_{N a} = 0.32638 m o l_{N_{2}} (\frac{2 m o l_{N a}}{3 m o l_{N_{2}}}) (\frac{22.9898 g_{N a}}{1 m o l_{N a}}) = 5.002267 g = 5.00 g

Example: Hydrogen gas can be generated by reaction of Zn metal with hydrochloric acid,

Zn(s) + 2HCl(aq) → ZnCl₂(aq) + H₂(g)

a) How many L of H₂ would be formed at 742 mmHg an 15°C if 25.5 g of zinc was allowed to react?

b) How many g of Zn would you start with if you wanted to prepare 5.00 L of H₂ at 350 mmHg and 30.0°C?

Partial Pressures: Mixture of Gases

As long as gases are inert (don't react each other), the total # mol, N, is the sum of the # of moles of each molecular species (n₁, n₂, ...)

Example: A 2.0 L O₂(g) and 8.0 L N₂(g), each at STP, are mixed. The mixture is compressed to occupy 2.0 L at 298K, what is the total pressure?

The situation is summarized by:

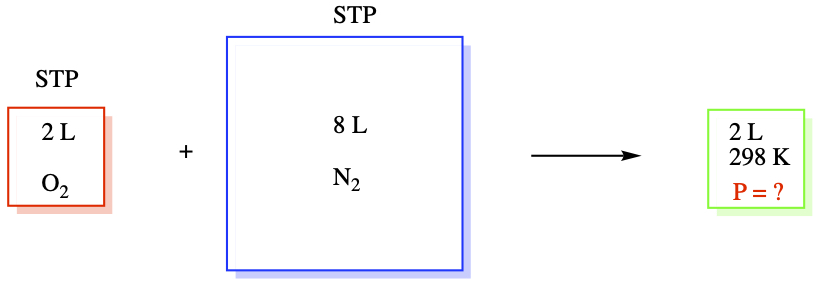
?mol_O2 = PV/RT = (1 atm)(2.0 L)/(0.08206 Latm/molK)(273.15K) = 0.089227 mol(O₂)

Similarly, n_N2 = 0.356909 mol. So, N = n(O₂) + n(N₂) = 0.446136 mol.

P = nRT/V =(0.446136 mol)(0.08206 Latm/molK)(298K)/2.0 L = 5.454878 atm = 5.4 atm

Partial Pressure

The sum of the component gas pressures of a gas mixture, is the total pressure of the mixture.

@ constant V and T,
P_total = P₁ + P₂ + P₃ + ...
with P_i is the partial pressure of i^th gas.

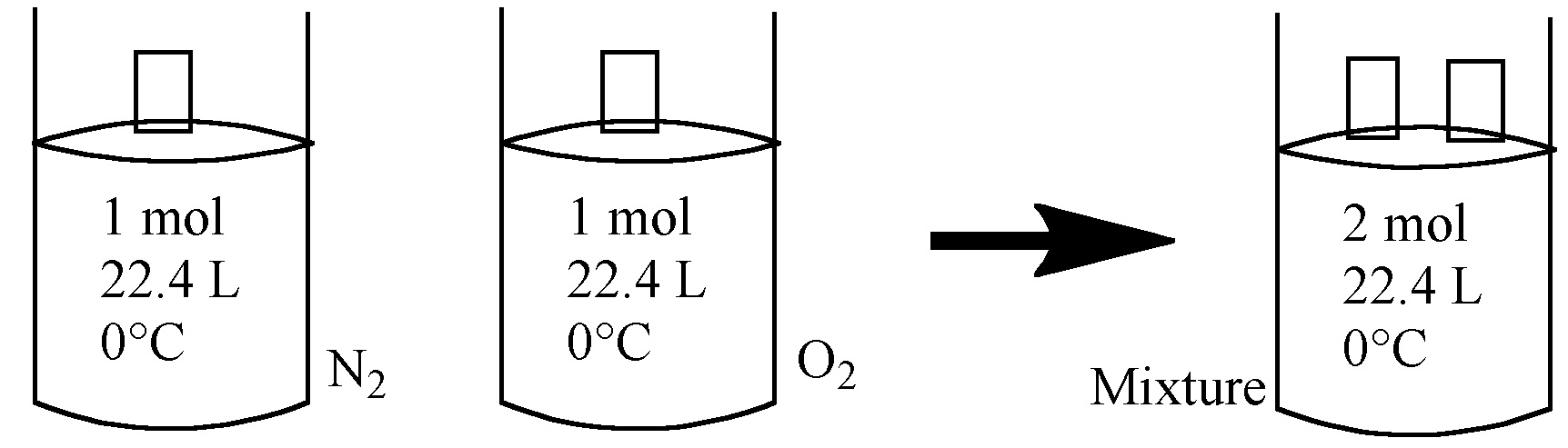
Let's suppose that we have N₂ @STP with the volume 22.4 L in one container. It means that we have 1 mol of N₂. In antoher container with its volume 22.4 L, we place O₂ @STP. So, it also contains 1 mol. Combine these gases, now we have 2 mol of gas, keeping volume V (22.4 L) and temperature T (0°c or 273.15 K) constant. The pressure should then be 2 atm.

So, combined gas has P_total = P_N2 + P_O2

The total pressure is, $P_{t o t a l} = \frac{n_{t o t a l} R T}{V}$

Furthermore, we have the relationship $P_{t o t a l} = \frac{n_{t o t a l} R T}{V} = \frac{(n_{N_{2}} + n_{O_{2}}) R T}{V} = \frac{n_{N_{2}} R T}{V} + \frac{n_{O_{2}} R T}{V} = P_{N_{2}} + P_{O_{2}}$

So, if we take the ratio between P_N2 to P_total you get,

$\frac{P_{N_{2}}}{P_{t o t a l}} = \frac{\frac{n_{N_{2}} R T}{V}}{\frac{n_{t o t a l} R T}{V}} = \frac{n_{N_{2}}}{n_{t o t a l}} = χ_{N_{2}}$

The ratio of mol of i^th component and the total # of moles is called mole fraction, χ_i. Then, we can calculate the partial pressure of N₂ by knowing χ_N2 and P_total as

$P_{N_{2}} = χ_{N_{2}} P_{t o t a l}$

Similar conclusion can be made for V_N2 / V_total = χ_N2 if we consider constant P and constant T.

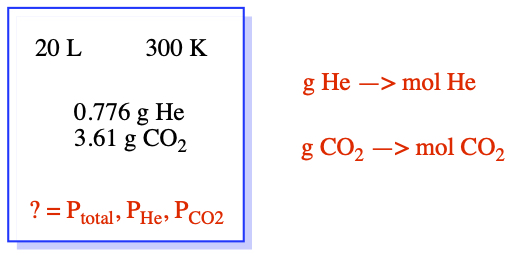
Example: In a 20.0 L flask, 0.776 g He and 3.61 g CO₂ are held at 300.0K. Calculate the total pressure and partial pressures of each gas.

We have, V and T. The total number of moles, n, can be calculated by converting the mass to mole. $\begin{array}{l} ? m o l_{H e} = 0.776 g_{H e} (\frac{1 m o l_{H e}}{4.003 g_{H e}}) = 0.19385 m o l_{H e} \\ ? m o l_{C O_{2}} = 3.61 g_{C O_{2}} (\frac{1 m o l_{C O_{2}}}{42.022 g_{C O_{2}}}) = 0.085907 m o l_{C O_{2}} \end{array}$ So, the total number of moles is 0.19385 + 0.085907 mol = 0.27975 mol.

$P = \frac{n R T}{V} = \frac{(0.2795 m o l) (0.08206 L a t m / m o l K) (300.0 K)}{20.0 L} = 0.34435 a t m$

The partial pressure is obtained from mole fractions. $\begin{array}{l} χ_{H e} = \frac{n_{H e}}{n_{t o t a l}} = \frac{0.19385 m o l}{0.27975 m o l} = 0.69294 \\ χ_{C O_{2}} = \frac{n_{C O_{2}}}{n_{t o t a l}} = \frac{0.085907 m o l}{0.27975 m o l} = 0.30708 \end{array}$

From these, we can get partial pressures $\begin{array}{l} P_{H e} = χ_{H e} P_{t o t a l} = (0.69294) (0.34435 a t m) = 0.23854 a t m = 0.238 a t m \\ P_{C O_{2}} = P_{t o t a l} - P_{H e} = 0.34435 a t m - 0.23854 a t m = 0.10574 a t m = 0.106 a t m \end{array}$

Example: The percent composition by volume of air is 78.08% N₂, 20.95% O₂, 0.930% Ar, and 0.0360% CO₂. What are the partial pressure, if barometric pressure is 748 mm_Hg (0.984210 atm).

Let's assume at the course of measurement, P, V, and T are constant. Consider Earth as a big container, and its volume doesn't change. Also, if one considers that average pressure at sea level to be fairly constant, we can justify that P, V, and T are constant. Then, we can say that,

$\frac{V_{i}}{V_{t o t a l}} = \frac{n_{i}}{n_{t o t a l}} = \frac{P_{i}}{P_{t o t a l}}$

It means that χs are

species	χ	P_i
χ_N2	0.7808	0.768 atm
χ_O2	0.2095	0.206 atm
χ_Ar	0.0093	0.00915 atm
χ_CO2	0.00036	0.000354 atm

The total pressure adds up to be 0.984 atm.

Example: A mixture of CS₂(g) and excess O₂(g) is placed in a 10.0 L reaction vessel at 100.0°C and a pressure of 3.00 atm. The reaction was carried out according to the following equation CS₂(g) + 3O₂(g) → CO₂(g) + 2SO₂(g)

After reaction, the temperature was returned to 100.0°C, and the mixture of CO₂, SO₂ and unreacted O₂ is found to have a pressure of 2.40 atm. What is the partial pressure of each gas in the product mixture?

Before the reaction was carried out, we have the values of P, V and T, therefore we can calculate the total number of moles of gases in the reactant mixture from PV = nRT. Similarly, we can calculate the total number of moles of gases in the products and excess O₂. Let us call n_react and n_prod for the respective number of moles.

Each of the gas molecules is stoichiometrically related. Before the reaction, the total number of moles of all gas species is,

n_react = n_CS₂ + n_O₂^reacted + n_O₂^excess

We also know the total number of moles of gases after the reaction,

n_prod = n_CO₂ + n_SO₂ + n_O₂^excess

Since 1 mol of CS₂ reacts with 3 mol O₂, producing 1 mol of CO₂ and 2 mol SO₂, we can rewrite the n_react and n_prod in terms of number of moles of CS₂, such that,

n_react = n_CS₂ + 3n_CS₂ + n_O₂^excess = 4n_CS₂ + n_O₂^excess n_prod = n_CS₂ + 2n_CS₂ + n_O₂^excess = 3n_CS₂ + n_O₂^excess

Now, in the above two equations, we have two unknowns. If we solve for n_O₂^excess in the second equation, we have,

n_O₂^excess = n_prod - 3n_CS₂

Substitute the above into the n_react equation, we get,

n_react = 4n_CS₂ + n_prod - 3n_CS₂

which is,

n_react = n_CS₂ + n_prod

Therefore, the number of moles of CS₂ is now,

n_CS₂ = n_react - n_prod = 0980 mol - 0.784 mol = 0.196 mol

Now that we know the number of moles of CS₂, we can relate all other species by stoichiometry in the reaction.

n_O₂^reacted = 3n_CS₂ = 3 (0.196 mol) = 0.588 mol

n_CO₂ = n_CS₂ = 0.196 mol

n_SO₂ = 2n_CS₂ = 0.392 mol

n_O₂^excess = n_prod - 3n_CS₂ = 0.784 mol - 3(0.196 mol) = 0.196 mol

From these, we can finally calculate the product mole fractions, χ.

χ_CO₂ = 0.196 mol / 0.784 mol = 0.250

χ_SO₂ = 0.392 mol / 0.784 mol = 0.500

χ_O₂^excess = 0.196 mol / 0.784 mol = 0.250

Now, partial pressure, P_i = P_total χ_i , of each gas is P_CO₂ = 2.40 atm (0.250) = 0.600 atm

P_SO₂ = 2.40 atm (0.500) = 1.200 atm

P_O₂^excess = 2.40 atm (0.250) = 0.600 atm

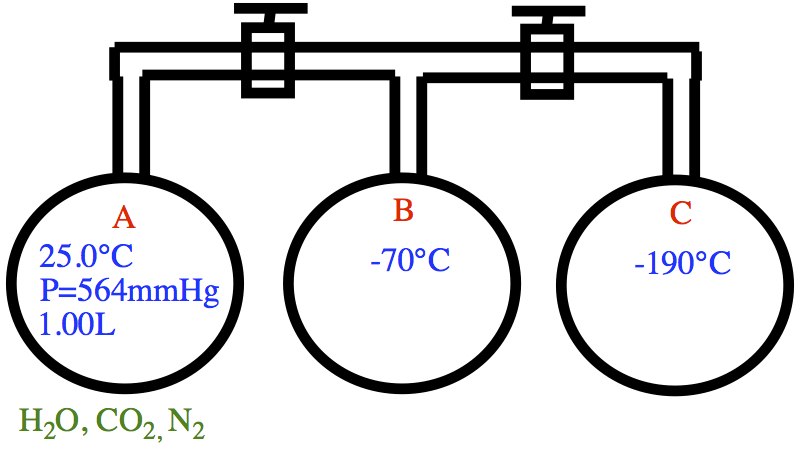
Example: In bulb A which has the volume of 1.00 L, a mixture of gas, H₂O, CO₂, and N₂ is placed. The valve between bulb A and bulb B is closed. Bulb B (1.00 L) is initially empty and is held at a temperature of -70°C. Bulb C (1.00 L) is initially empty and is held at -190°C. We also know that CO₂ sublimes at -78°C, and N₂ boils at -196°C. a) When the valve between A and B is open, then the pressure becomes 219 mmHg. What do bulbs A and B contain? b) How many moles of H₂O are in the system? c) Both valves are now open, and the measured pressure is 33.5 mmHg. What do bulbs A, B, and C contain? d) How many moles of N₂? e) How many moles of CO₂?

The situation is this:

a) From the initial condition, we can calculate the total number of moles of gases.

n = \frac{P V}{R T} = \frac{(0.742 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (298.15 K)} = 0.03033 m o l

Since bulb B is held at -70°C all H₂O is frozen in bulb B. Therefore, there must be CO₂ and N₂ are the only ones found in bulbs A and B.

b) To calculate the number of moles of H₂O, we need to know the number of moles of gas in bulb A and bulb B separately since these two bulbs have different temperature.

The pressure in both bulbs is $? a t m = 219 m m H g (\frac{1 a t m}{760 m m H g}) = 0.2882 a t m$ So, in bulb A, $n_{A} = \frac{P V}{R T} = \frac{(0.2882 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (298.15 K)} = 0.01178 m o l$ In bulb B, $n_{B} = \frac{P V}{R T} = \frac{(0.2882 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (203.15 K)} = 0.01729 m o l$ The total number of gas molecules are then, n_total = 0.029068 mol. Then, the number of moles of water is 0.03033 mol - 0.029068 mol = 0.001262 mol = 1.26 x 10^-3 mol.

c) Now all valves are open. P in each bulb is 33.5 mmHg = 0.04408 atm. Since bulb C is -190°C, CO₂ is frozen. So then the contents of each bulb are: bulb A == only N₂, bulb B == N₂ and H₂O, and bulb C == N₂ and CO₂.

d) As in part b), we can calculate the number of moles of N₂ in each bulb, as $\begin{array}{l} n_{A} = \frac{P V}{R T} = \frac{(0.04408 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (298.15 K)} = 0.0018017 m o l \\ n_{B} = \frac{P V}{R T} = \frac{(0.04408 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (203.15 K)} = 0.0026444 m o l \\ n_{C} = \frac{P V}{R T} = \frac{(0.04408 a t m) (1.00 L)}{(0.08206 L a t m / m o l K) (83.15 K)} = 0.0064602 m o l \end{array}$ The total number of moles of gas, which is N₂, is 0.010906 mol.

e) The number of moles of CO₂ is

$n_{C O_{2}} = n_{o r i g i n a l} - n_{H_{2} O} - n_{N_{2}} = 0.03033 m o l - 0.001262 m o l - 0.010906 m o l = 0.01816 m o l$

Collecting gas over water

Experimentally, a convenient set-up for collecting gaseous species are often done over the water, as shown below.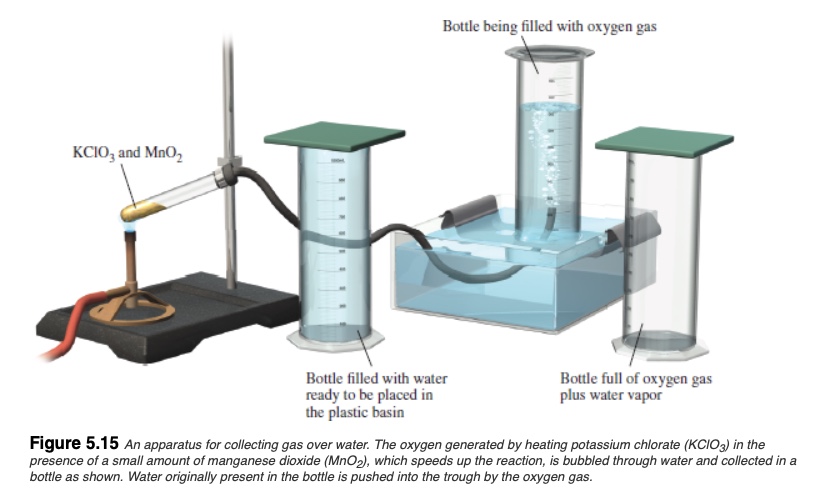

The collected gas contains water vapor, thus exerts pressure in addition to the collected gas. You can see in the following table that at different temperature the vapor pressure of water changes. In obtaining the properties of the collected gas, one needs to subtract out the vapor pressure of water from the measured, often, barometric pressure.

Kinetic Theory of Gases

IGL at molecular level -- meaning of kinetic energy (thermal energy)

Our model

Large # (in the order of 10²³) of molecules in constant and random motion

Molecules collide each other and to the wall to change direction, otherwise straight-line motion

Gas molecules are sparsely separated, so that the volume is mostly empty space

No force b/w molecules

Individual molecules can gain and lose energy, but the total energy is constant

Using this model we can derive the expression for pressure,

$P = \frac{1}{3} \frac{N m {〈 υ 〉}^{2}}{V}$

where N is the # of molecules, m is the mass of the molecule in amu <ν> is the average velocity of gas, and V, is the volume of the container.

If you want to see the derivation of the pressure expression, click below!

+ Derivation of P

From Newton's law of motion, F = ma where, F is the force acting on a particle with mass m, and a is the acceleration, and a is the change in velocity, ν, with respect to time, t. Thus, we have F = (mν)/t. The gas molecule is placed in a cubic box with the side length, ℓ, as shown. The numerator, mv is momentum, and the momentum change in the particle for one cycle of collisions to the wall (back and forth b/w two walls) in the x direction is twice the momentum. Because Δp = mv_- - mv₊ ["-" ("+")in the motion toward left (right)], but the speed of the particle is the same; only the direction is opposite, so Δp = mv_- - (- mv_-) = 2mv_-.
$F = m a = \frac{m Δ v}{Δ t} = \frac{(m v - (- m v))}{Δ t} = \frac{2 m v}{Δ t}$

The time it takes to complete one cycle is, t = 2ℓ/v. If we substitute this into F = 2mv/t, i.e.

F = 2 m v \frac{v}{2 l} = \frac{m v^{2}}{l}

Since pressure P = F/A,

P = \frac{m v^{2}}{l A} = \frac{m v^{2}}{V}

Each partilce contributes to the pressure, therefore, each particle velocity must be taken into account,

P = \frac{m (v_{1}^{2} + v_{2}^{2} + v_{3}^{2} + \dots)}{V}

Instead of expressing every particle velocity, we can use the average velocity of all particles,

{〈 v 〉}^{2} = \frac{v_{1}^{2} + v_{2}^{2} + v_{3}^{2} + \dots}{N}

and rerrange to solve for the individual particle velocity, you have

v_{1}^{2} + v_{2}^{2} + v_{3}^{2} + \dots = {〈 v 〉}^{2} N

Substitute this expression into the pressure expression, one obtains

P = \frac{m {〈 v 〉}^{2} N}{V} \to \frac{m {〈 v 〉}^{2} N}{3 V}

The last arrow indicates that velocity has three components (x, y, z), and has to be taken into account. So, this is the desired result.

Example: If one mole of CH₄ gas at 1.00 atm and its volume = 22.4 L, what is the average velocity of the gas?

Let us first solve for in the above equation, $〈 v 〉 = {(\frac{3 P V}{N m})}^{1 / 2}$ By using the conversion factor of 1 atmL = 101.3 J, and considering the fact that the mass of methane is 16.04 amu, $〈 v 〉 = {(\frac{3 P V}{N m})}^{1 / 2} = {(\frac{3 (22.4 a t m L) (\frac{101 . J}{1 a t m L})}{(6.022 \times 10^{23}) (16.054 a m u) (\frac{1.660454 \times 10^{- 27} k g}{1 a m u})})}^{1 / 2}$ Since there is 1 mole of CH₄, which means that N = 6.022 X 10²³ molecules. Also, in above, we used the definition of 1 amu = 1.660454 X 10^-27 kg. $〈 v 〉 = {(\frac{6807.36 J}{160.54 k g} \times 10^{4})}^{1 / 2} = 651.2 m / s$

Looking at the equation above, we see that PV in the numerator can be replaced by nRT, as we're still dealing with the ideal gas. Then, we have, $〈 v 〉 = {(\frac{3 P V}{N m})}^{1 / 2} = {(\frac{3 n R T}{N m})}^{1 / 2} = {(\frac{3 R T}{μ})}^{1 / 2}$ The last equal sign is given by recognizing that Nm/n is the molar mass of the molecule, since m is the mass of the individual molecule, and if we have one mole (hence 6.022 X 10²³ of them), the term is the molar mass.

Meaning of Kinetic Energy

From Newton's law of motion, we know that kinetic energy, E_K = 0.5 mv², we can derive expression for kinetic energy for gas,

E_{K} = \frac{3}{2} R T

with R = 8.314 J/molK (another way to express the gas constant, also 1 J = 1 kgm²/s). So, for a gas kinetic energy depends only on the temperature. Conversely, temperature measures the how much motion the molecules possess.

+ Derivation of Kenetic Energy

Starting with the expression of the pressure.

P = \frac{1}{3} \frac{N m {〈 v 〉}^{2}}{V}

P V = \frac{1}{3} N m {〈 v 〉}^{2}

Since PV = nRT, we have

n R T = \frac{1}{3} N m {〈 v 〉}^{2}

Kinetic energy is given by E_k = ½mv² and mv² = 2E_k.

n R T = \frac{2}{3} N E_{k}

If you suppose that N, the number of molecules, is expressed in terms of mole, then N → n. Therefore,

n R T = \frac{2}{3} n E_{k}

Solve for E_k, we get

E_{k} = \frac{3}{2} R T

Kinetic energy of gas depends only on temperature!
If T → 0, E_K → 0

Furthermore, the average speed of the gas molecules, as obtained above, is
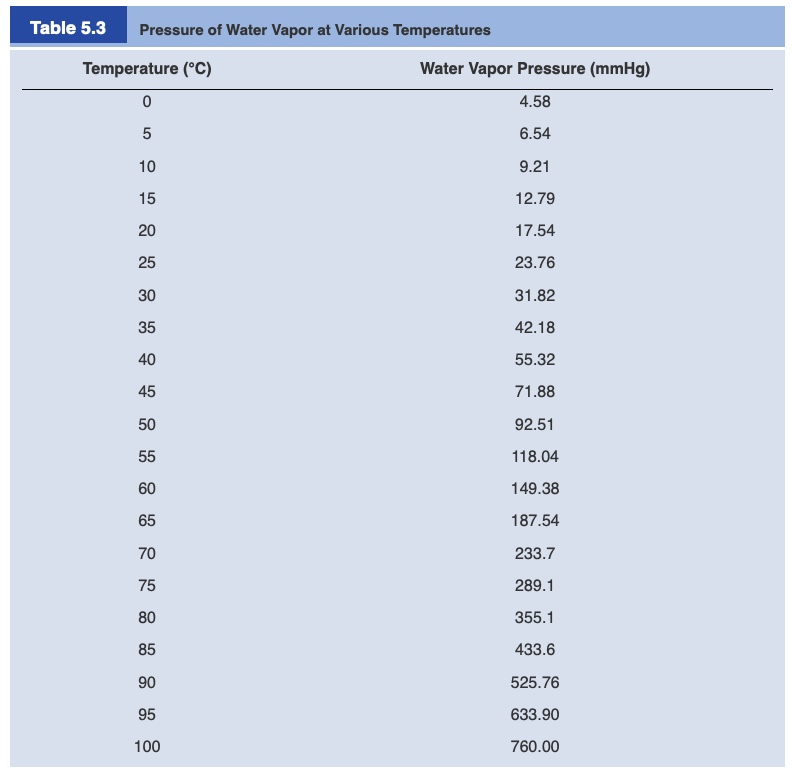
$〈 v 〉 = {(\frac{3 R T}{μ})}^{\frac{1}{2}}$ Therefore, the speed of molecule depends on the molar mass and temperature. Heavier the molecules, slower the speed at given temperature. The speed is higher at higher temperature.

The following figure illustrates the how molecular speed is distributed among the population of gases and at different temperature.

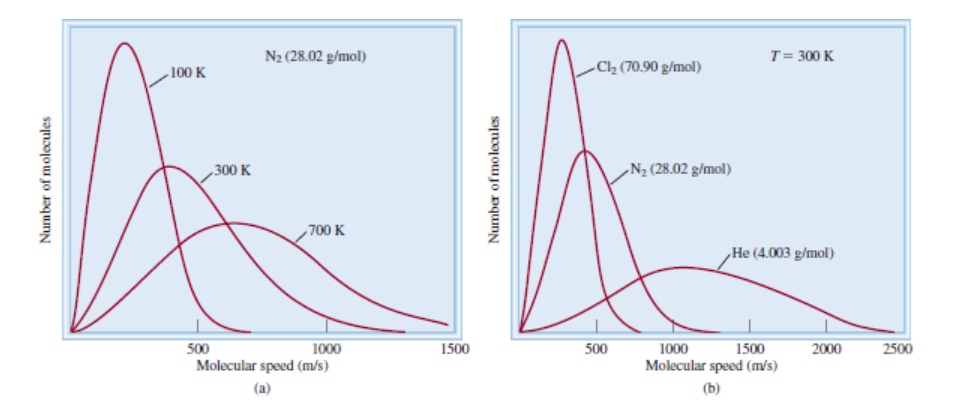
On the left is the speed distribution of N₂ molecules at different temperature. As you it can be seen, the peak shifts to lower speed when the temperature is lowered. Also at higher temperature, the distribution becomes broader.

The panel on the right shows at one temperature, distribution of different molecules, hence the molar masses, pare plotted. Lighter molecules have broader distribution while the heavier molecules have sharper distribution.

Example: The cruising speed of Boeing 747 jet is 570.0 mi/hr. What temperatures does butane (C₄H₁₀) gas, used in cigarette lighter, have the same speed? By the way, don't smoke! It's not good for you!

The volocity in m/s unit is more appropriate than mi/hr. $? \frac{m}{s} = 570 \frac{m i}{h r} (\frac{1.60934 k m}{1 m i}) (\frac{10^{3} m}{1 k m}) (\frac{1 h r}{60 \min}) (\frac{1 \min}{60 s}) = 158.3 k m / s$

The following is nearly the same question as above.

Example: The escape velocity required for gas molecules to overcome the earth's gravity and go off to outer space is 1.12 x 10³ m/s at 15°C. Calculate the molar mass of a species with that velocity. Would you expect to find He and H₂ molecules in the earth's atmosphere? What about argon atom?

Gas Diffusion and Effusion

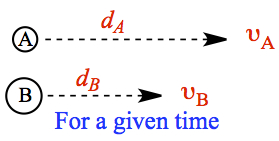
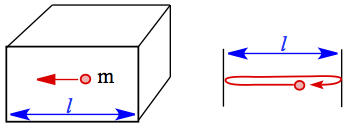
Diffusion - migration of molecules due to random motion

Effusion - escape of molecules under low pressure

Consider two molecules, lighter A and heavier B, moving in one direction, as shown on left. For a given time interval, distances covered by the molecules differ according to the velocity equation, which depends on molar mass. Lighter molecule travels further for a give time interval, if the two gases are at the same temperature. We can obtain the relationship between the distance traveled is given by the following ratio. $\frac{ν_{A}}{ν_{B}} = \frac{{(\frac{3 R T}{μ_{A}})}^{\frac{1}{2}}}{{(\frac{3 R T}{μ_{B}})}^{\frac{1}{2}}} = {(\frac{μ_{B}}{μ_{A}})}^{\frac{1}{2}}$ This is called Graham's law of diffusion

We can use this equation to have a subway (molecule) race, just as seen at the Yankee stadium, between molecules!

Seen at New York magazine.

Example: When gaseous ammonia and HCl meet, they form a complex NH₄Cl, and appear as white cloud. In the tube shown here, concentrated solution of ammonia is place 2 m away from the concentrated HCl. Where do they meet to form white cloud (blue in the figure!)?

Let us define distance covered by HCl as x. Then, the distance covered by NH₃ is 2 - x. Since reaching time is the same, the ratio of speeds is the ratio of the distances covered by each.

\frac{ν_{H C l}}{ν_{N H_{3}}} = \frac{x}{2 - x} = {(\frac{μ_{N H_{3}}}{μ_{H C l}})}^{\frac{1}{2}}

Then, solve for x, one gets

x = \frac{2 {(\frac{μ_{N H_{3}}}{μ_{H C l}})}^{\frac{1}{2}}}{1 + {(\frac{μ_{N H_{3}}}{μ_{H C l}})}^{\frac{1}{2}}}

Then, substitute the molar masses in, you get the cloud formation at x = 0.812 m (closer to HCl).

Deviation from Ideal Behavior

Ideal gas assumptions:

No volume associated with gas molecules

No interactions between molecules -- which affects pressure

These assumptions fail at high pressure, as shown below!

The plot is drawn so that compressibility, (PV_m/RT), is plotted against pressure, P. V_m is the molar volume; volume of 1 mol of gas.

If the gas behaves as ideal, meaning that it follows IGL, the gas would follow the blue curve. However, real gases behave quite differently at high pressure.

If one takes into account of the excluded volume and molecular interactions, one can obtain the following eqn, called van der Waals' eqn. $(P - \frac{a n^{2}}{V^{2}}) (V - n b) = n R T$ where a and b are the constants specific to gas molecules.