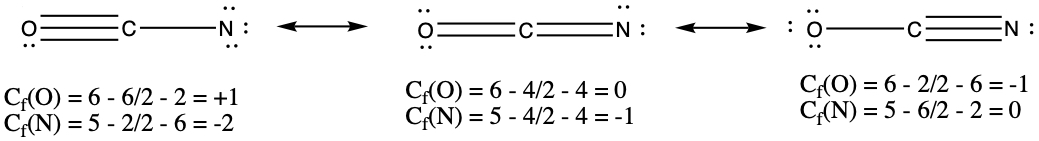Chapters 7-10. The Electronic Structure of Atoms to Chemical Bonding

Light and the Electromagnetic Spectrum

Light

Light is important in chemistry partly because light can determine structures and properties of molecules. There are many examples of using light for different purposes in our daily lives. For example, microwave oven uses the property of microwave (~100 mm wave length) to boil water. The MRI technique uses radio wave close to analog TV wave (VHF and UHF) in wave length to image the water content in your body. There are many many others.

Electronmagnetic Spectrum

We know what happens when the light passes through a prism. The white light separates into different colors, as shown in the figure below. The separated colors are generally called spectrum.

Each color is represented in terms of a wave. There are two characteristics of wave.

Wave Length (λ) — peak to peak distance (wave in coordinate space)

Frequency (ν) — # of peaks passing through time(wave in time domain)

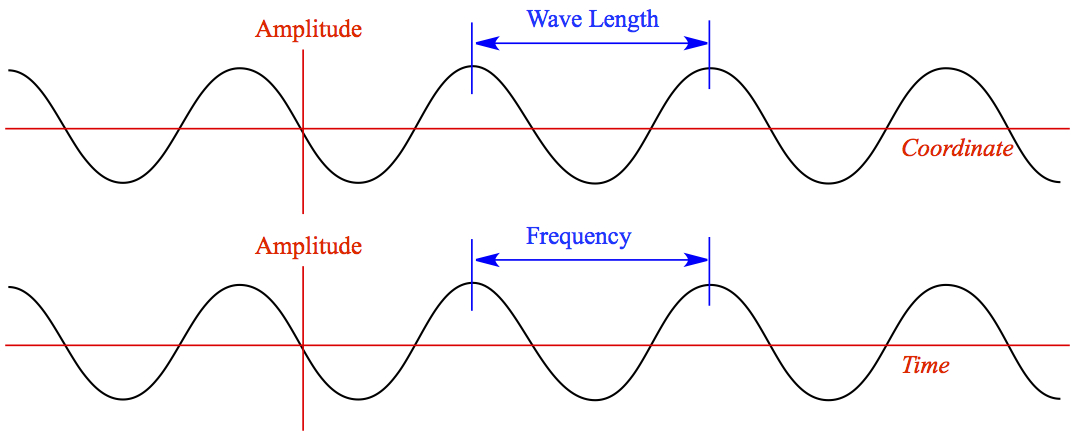
The unit of wave length is in the length unit, such as m.

The unit of frequency is in the recipical of time, such as /s (also called Herz or Hz)

Therefore, if these two units are multiplied, it becomes the speed, (length/time). For all electromagnetic waves, the frequency x wave length is always speed of light (2.998 x 10⁸m/s)

c = λ ν

It means that λ and ν are in the recipical relationship.

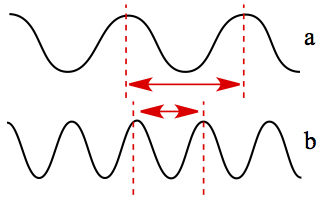
The wave length is longer in case a than that in case b. It also means that case b has higher frequency than in case a.

The following figure shows the length scale of electromagnetic waves with objects of the corresponding size. (Taken from this site.)

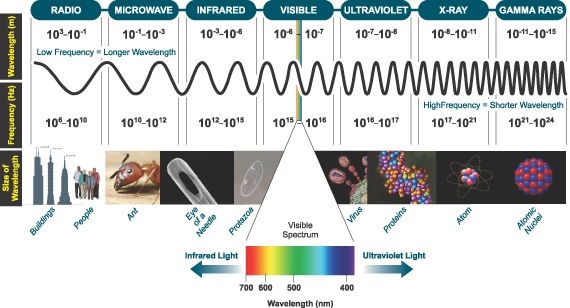
As you can see, the visible light, for which our eyes can detect, is only a very tiny window of the electromagnetic spectrum.

As the name electro-magnetic implies that the wave of this kind is consist of electric field and magnetic field. In a sense, each field induces the other, and pushing each other to propagate the wave. The following figure shows the interweaving of electric field and magnetic field for propagation of light pictorially.

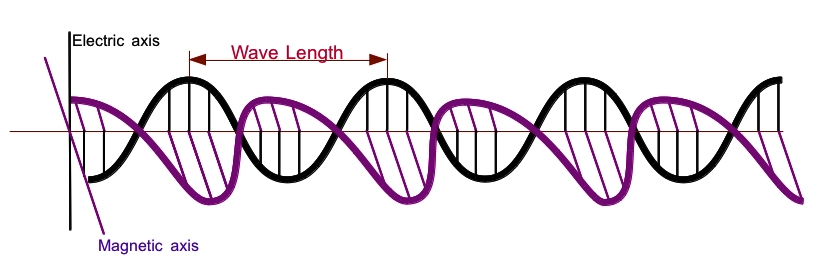
The electric field and magnetic field are perpendicular to each other and the direction of propagation is to the right.

Photoelectric Effect

I just said above that light is a wave. In the following light is explained by a particle. In the photoelectric effect, light is used to eject electron from a metal plate, which travels to the positively charged electrode so that the electrical current is produced. The electric current is registered in an ampmeter.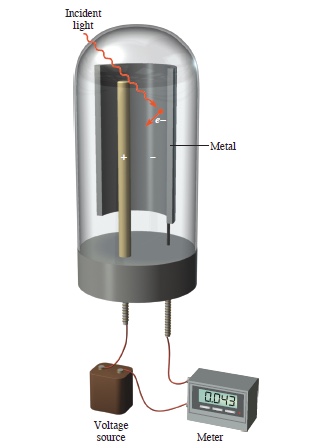

Einstein explained the phenomena by using Planck's idea five years prior, where Planck stated that the energy of a photon, a particle of light, is given by $E = h ν$ where h is called Planck's constant today and has a value 6.626 x 10^-34Js. Using this, Einstein explained the photoelectric effect by $E_{k} = h ν - W$ where E_k is kinetic energy of the ejected electron and W is so-called work function.

Electromagnetic Energy and Atomic Line Spectra

When the sun's light is passed through a prism, as you know, the color separates. Let's say that you have a precision instrument to separate the color into much more details than a simple prism can do. Upon analyzing the color in the Sun's light, you see the dark band or missing color at certain wave lengths. Such dark lines are called absorption line spectra. The instrument used to observe the spectral lines are something like the following:

Fraunhofer Society The sun light enters behind us, and directed into the prism on the rotating disk that angle can be chosen so that the portion of the solar spectrum enters into what appears to be a telescope, generally referred to as spctroscope. When the selected part of the sun light is observed at the other end of the spectroscope, the some colors are interrupted by dark lines, as shown below. These are the absorption lines.

Look at the following figure. This figure is the spectrum of sun's ray taken with the precision instrument in the visible light range.

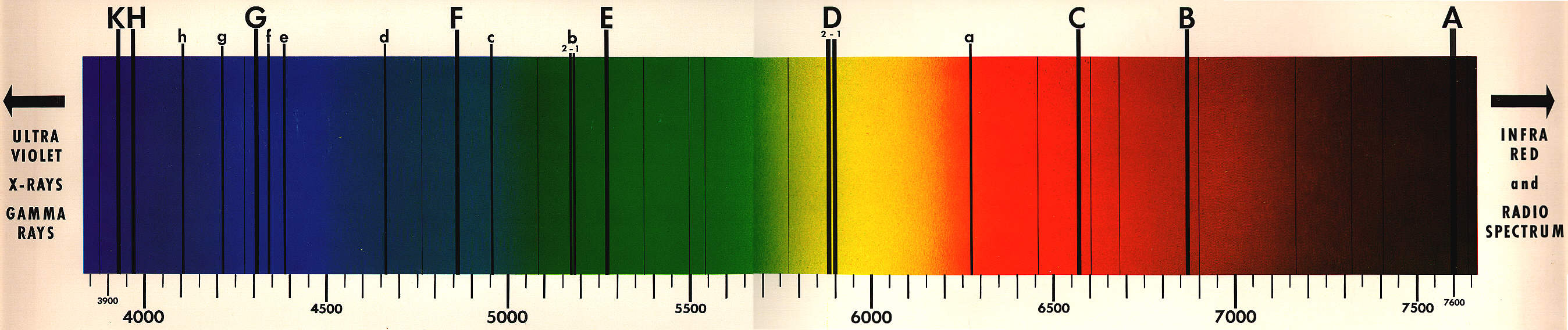
To the right of the figure wave length increases, and the scale is in the unit of Ångström, Å (1 Å = 10^-10 m). The dark bands are clearly visible. So, what do the dark lines represent? These lines puzzled the scientists since 1814 (earlier by Wollaston in 1802). However, the mystery was slowly unraveling, starting with the laboratory reproduction of the line spectra.

In the laboratories, experiments similar to the following figure had been done.

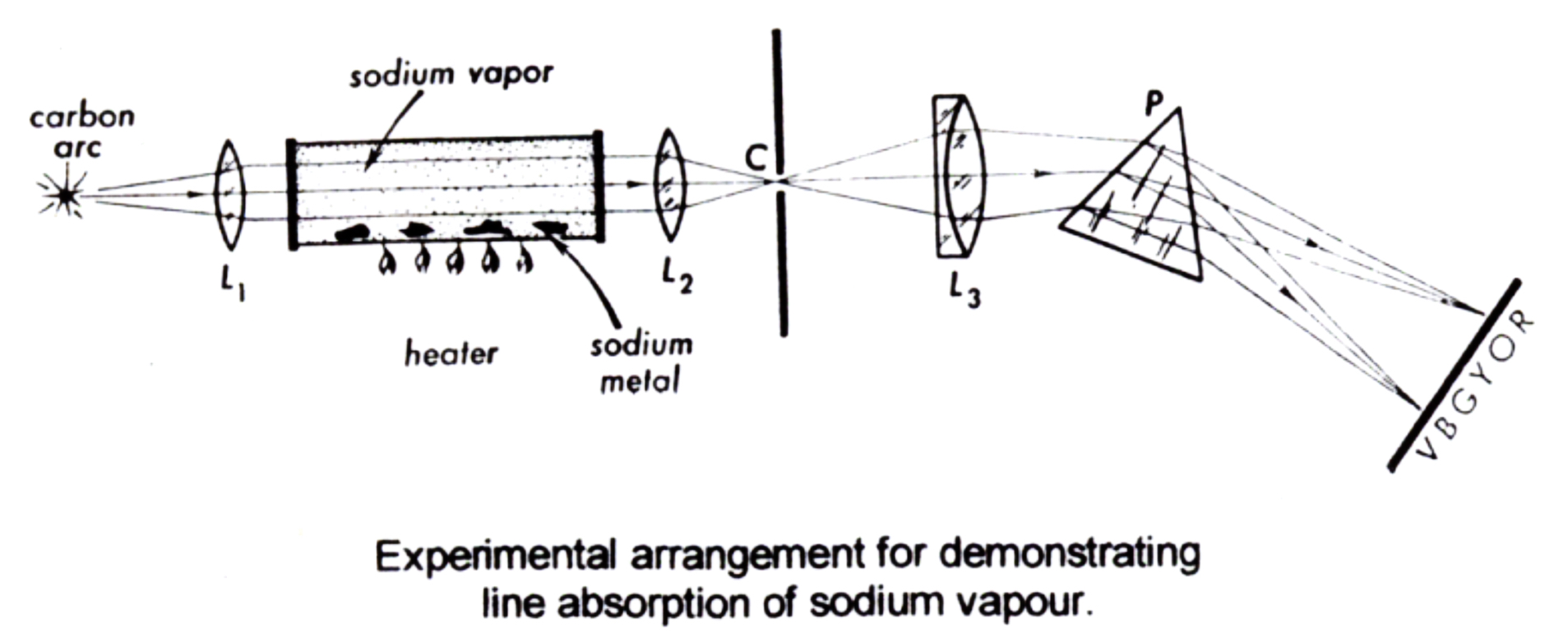
In this example, the heater vaporizes Na atom in the sealed glass tube, and shine the light from the carbon arc lamp onto the tube, one can reproduce the two dark bands, labeled as D above, in the solar spectra.

It means that sun is made up, at least partially, of sodium! The consequence of this finding is obvious! The Earth may not be as unique as we thought it was.

Mathematical relationship of wave length with misterious whole number!

Scientists started to find the patterns of other elements in the Sun's ray. What do those pattern tell us? What they started to see, was that there was a relationship between wave length and integers!

Balmer came up with the following, called Balmer equation:

Wave Length	Frequency
$\frac{1}{λ} = R_{\infty} [\frac{1}{2^{2}} - \frac{1}{n^{2}}]$	$ν = R_{\infty} c (\frac{10^{9} n m}{m}) [\frac{1}{2^{2}} - \frac{1}{n^{2}}]$

In these equations R_∞ is what is known today as Rydberg constant (1.097 x 10^-2 nm^-1), c is the speed of light, and n is an integer larger than 2. Be careful with conversion, as R_∞ unit is different from c! In the frequency equation, the extra factor of 10⁹ nm/m is used to convert the nm^-1 unit in the R_∞ into m^-1 unit so that the frequency comes out in the Hz (s^-1) unit.

Rydberg then generalized Balmer's equation to fit all line spectra of hydrogen. Thus, we have the Balmer-Rydberg equation

Wave Length	Frequency
$\frac{1}{λ} = R_{\infty} [\frac{1}{m^{2}} - \frac{1}{n^{2}}]$	$ν = R_{\infty} c (\frac{10^{9} n m}{m}) [\frac{1}{m^{2}} - \frac{1}{n^{2}}]$

with m < n.

It works great with hydrogen atom, but nothing else. They have to wait another 30 years or so to fully comprehend where the atomic spectral lines come from. However, some partial answers had started to come out, particularly the relationship between the line spectra and the structures of atom by Niels Bohr.

Particle-like Properties of Electromagnetic Energy

So, we said above that electromagnetic wave is a wave with frequency and wave length. It is a wave! Einstein, however, said in 1905 (annus mirabilis) that he could explain the phenomenon called "photoelectric effect" if he used light being particles! Einstein used the idea from Planck whose seemingly desparate theory to explain the so-called black-body radiation through a packet of energy (particle of energy), called a quantum.

In his theory, Planck considered the energy of a light particle, called photon, depends on the frequency of light, given by the following equation.

E = h ν

where h is Planck constant (h = 6.626 x 10^-34Js, very tiny number!), and since c = λ ν, the energy of light particle is associated with the wave length, as

$E = \frac{h c}{λ}$

What's important here is that the electromagnetic radiation is both wave and particle, wave-particle duality.

Tentative structure of atom: Bohr atom

Physicists then wanted to understand why atom is stable. At the time, they only new atom has a heavy nucleus with + charge and electrons with - charge, are around nucleus, according to Rutherford (Chapter 2). You know that + charge and - charge attract each other. If an electron with a negative charge is zipping initially around a nucleus with positive charge, the electron should start to spiral down to nucleus by emitting light of higher and higher frequency, as speeding up toward the nucleus. And, eventually, the electron would collide with nucleus, and the atom would disappear. 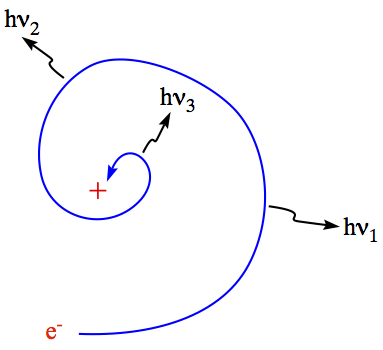This is the scenerio that the classical electromagnetism tells us. (See the figure on right.)

What it means is that atom is not stable in terms of classical physics! It also means that we needed a new and fundamental mechanics for atomic and subatomic processes!

Bohr in 1914 gave the partial answer to the structure of atom, and simultaneously solved hydrogen atomic spectral lines. His idea was hinted from Rutherford's nuclear atom. Bohr was able dervie an mathematical expression for state of hydrogen atom, as having a number of definite and stable orbits that are permanent. Electrons in atoms then circumnavigate the nucleus on these orbits. The state of hydrogen atom is decided by a single integer, n, as shown below,

$E_{n} = \frac{{− R}_{H}}{n^{2}}$ where R_H is called Rydberg constant (1312 kJ/mol, or 2.18 x 10^-18J).

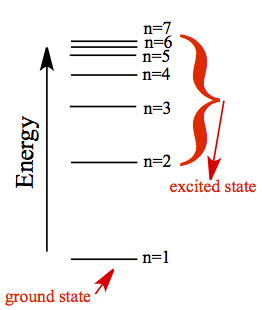
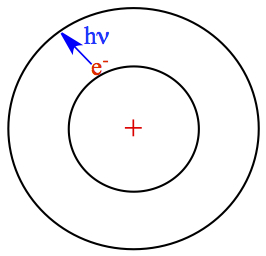
The figure on left shows the atomic structure according to Bohr. Since there are stable orbits, and in order for the electron to go to higher orbit, say n = 2 state (or any other n except for n=1 is called excited state ), from its lowest energy state (ground state with n = 1), the jump (it is called transition) must be accompanied by an absorption of a photon of energy with E = h ν. This jump is what is known as quantum jump! Atom absorbs specific frequency of light to make a quantum jump.

Now, we can explain why Balmer-Rydberg equation only has integers. According to Bohr, the difference between the energies of the two states correspond to the quantum jump with photon energy, E_photon = h ν = ΔE_nm. The last term, ΔE_nm is the difference between the two states where m labels the lower energy of the two states, and n labels the higher.

$E_{p h o t o n} = h ν = Δ E_{m n} = E_{n} - E_{m} = h c R_{\infty} N_{A} (\frac{10^{9} n m}{1 m}) [\frac{1}{m^{2}} - \frac{1}{n^{2}}] = R_{H} [\frac{1}{m^{2}} - \frac{1}{n^{2}}]$

This equation completely solves the atomic spectra of hydrogen.

Example: What is the energy in kJ/mol of photon being absorbed for transition between n = 1 and n = 2?

Using the above equation, we have $E_{p h o t o n} = h c R_{\infty} [\frac{1}{m^{2}} - \frac{1}{n^{2}}]$

we have m = 1 and n = 2. Since the answer is expressed by per mole quantity, we need to multiply the above by Avogadro's number.

$E_{p h o t o n} = h c R_{\infty} [\frac{1}{m^{2}} - \frac{1}{n^{2}}] N_{A}$

Place all the constants in with units, we have a $E_{p h o t o n} = (6.626 \times 10^{- 34} J s) (2.998 \times 10^{8} m / s) (1.097 \times 10^{- 2} \frac{1}{n m} (\frac{10^{9} n m}{1 m})) [1 - 0.25] (6.022 \times 10^{23} / m o l)$

$E_{p h o t o n} = 98.421 \times 10^{4} J / m o l = 984.2 k J / m o l$

Depending on the lower states of the two integers in the Balmer-Rydberg equation, the state with label m, the spectra are assigned as spectral series.

Name	Lower state	Region
Lyman Series	m = 1	Ultraviolet
Balmer Series	m = 2	Visible
Paschen Series	m = 3	Infrared
Brackett Series	m = 4	Infrared
Pfund Series	m = 5	Infrared
Humphreys Series	m = 6	Infrared

Example: What is the upper state n in the Balmer series that emitted a photon with its energy 275.6 kJ/mol?

In the Balmer series, the lower state, m = 2. Since we have the energy of photon absorbed, all we need to do is to rearrange the following equation and solve for n,

$E_{p h o t o n} = R_{H} [\frac{1}{m^{2}} - \frac{1}{n^{2}}]$ for which we know E_photon, and R_H. To isolate n, you need to do the following, $\frac{E_{p h o t o n}}{R_{H}} = \frac{1}{m^{2}} - \frac{1}{n^{2}}$ Here we know m = 2, then, $\frac{1}{n^{2}} = \frac{1}{2^{2}} - \frac{E_{p h o t o n}}{R_{H}}$ Then, the recipical of the equation is, $n^{2} = \frac{1}{\frac{1}{2^{2}} - \frac{E_{p h o t o n}}{R_{H}}}$ $n = \sqrt{\frac{1}{\frac{1}{2^{2}} - \frac{E_{p h o t o n}}{R_{H}}}} = \sqrt{\frac{1}{\frac{1}{2^{2}} - \frac{275.6 k J / m o l}{1312 k J / m o l}}} = 5.00$ Therefore, the transition was from m = 2 to the n = 5 state.

Wave-like Properties of Matter

Having seen wave is described by particle, de Broglie thought that the opposite might be true. It means that, this tiime, particle can be considered as wave. Oh, why not!? So, he derived an equation relating the characteristics of wave and particle in the following way:

We already established that $E = \frac{h c}{λ}$

Therefore, $λ = \frac{h c}{E}$

and from Einstein's E = mc², we have $λ = \frac{h c}{E} = \frac{h c}{m c^{2}} = \frac{h}{m c} \to \frac{h}{m v}$

Since c, the speed of light, is a velocity, we can substitute v, velocity of particle, in place of c. The denominator in the last term, mv, is a linear momentum, which is associated with particle of mass m moving at the speed v. Weird cool, right?

Example: What is the de Broglie wave length of electron in 1s orbital in hydrogen atom, if its average velocity was 0.730 % of the speed of light? Compare the value obtained to the wave length of Usain Bolt who can run a 100 m dash in 9.58 s, if he weighs 94.0 kg.

The speed of light is 2.998 x 10⁸ m/s, and the mass of an electron is 9.11 x 10^-31 kg. $λ = \frac{h}{m v}$

$λ = \frac{h}{m v} = \frac{6.626 \times 10^{- 34} J s}{9.11 \times 10^{- 31} k g \cdot (0.00730 \cdot 2.998 \times 10^{8} m / s)} = 3.32 \times 10^{- 10} m = 3.32 \overset{\circ}{A}$ The symbol Å, angstrom, is a distance unit of 10^-10 m. So, this wave length corresponds to the atomic scale. Since the average radius of hydrogen atom is 0.529 Å, the circumnavigation of electron is 3.32 Å and matches with our calculated value.

As for Usain Bolt, the calculation is straight forward. His wave length is then,

$λ = \frac{h}{m v} = \frac{6.626 \times 10^{- 34} J s}{94.0 k g (\frac{100 m}{9.58 s})} = 0.6753 \times 10^{- 32} m$

So, for a macroscopic particle, the de Broglie wave length is very very small. The effect of wave nature of us is not even detectable; it is even smaller than the atomic scale!! On the other hand, for a hydrogen atom, the wave length is the same scale as the atomic scale, and therefore the duality of wave and particle exists.

Example: What is the wave length, in m, of α particle with kinetic energy of 8.0 x 10^-13 J. The mass of α prticle is 4.00150 amu (1 amu = 1.67 x 10^-27 kg.

Quantum Mechanics and the Heisenberg Uncertainty Principle

So far, we have established:

All electromagnetic waves for different purposes (such as nuking your coffee or getting chest X-ray), differ only by wave length.

Wave is particle.

Particle is wave.

Heisenberg's Uncertainty Principle

Weirdness doesn't stop here. One of the corner stones of quantum mechanics is Uncertainty principle of Heisenberg. The principle sharply separates the ideas of the classical world (pre-quantum era) and the quantum world.

When a baseball is thrown out of the hand of a pitcher, you can track how the ball is traveling. If you are a good baseball player and if you know what kind of pitch the pitcher would throw, you can perhaps hit the ball hard. This is partly because you can track the ball with your eyes and your brain computes the ball's trajectory. The trajectory is a notion completely mathematically definable using initial speed and direction (velocity), as well as initial position of the ball. So, trajectory needs position and velocity. This is classical world.

In a microscopic world the notion of trajectory must be rejected, said Heisenberg. Here he establishes one of the most fundamental aspect of the quantum world through his Uncertainty Principle.

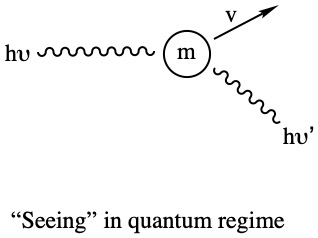
Heisenberg's idea is that the motion of quantum particles, such as electrons, protons, photons, etc., are fuzzy. If you know more about the position, you would lose the exactness of speed and its direction. On the other hand, if you know more about the velocity (speed and direction), you know less about where the particle is. That's way too weird!! Anyway, Heisenberg put his idea into mathematical form: $(△ x) (△ m v) \geq \frac{h}{4 π}$

It tells you that the products of uncertainty in measurement of coordinate, Δx, and uncertainty in the measurement of momentum (velocity), Δmv is always greater or equal to Planck's constant, h/4π. This inequality gives the fuzziness in the motion of subatomic particles.

Weird!

Wave Functions and Quantum Numbers

Mathematical foundation of quantum mechanics was layed by Heisenberg in 1924. Soon after, Heisenberg's advisor and his colleague quickly established what is known today as matrix mechanics. In 1926, Schrödinger established his so-called wave mechanics. It was argued among the physcists of the day which one is correct formulation of quantum mechanics. Schrödinger later showed the equivalency of the two formulations. Here is his equation that bares his name,

\hat{H} Ψ = E Ψ

Schrödinger Equation

It doesn't really matter what it really means, but we just look at the result of solving this equation. The function Ψ is called wave function, and E is the energy.

Quantum mechanics can be applied to different systems at substomic and molecular levels. Since in this chapter we are dealing with atomic structure, we are going to look at the Schrödinger's result to hydrogen atom and its spectra.

When solving the Schrödinger equation, one obtains 3 sets of integers and a set of half-integers, called quantum numbers.

m_l

m_s

What's interesting about these sets of numbers, is that they describe the structure of atoms. These numbers completely describe the state of atom.

Principal Quantum Number, n

This quantum number describes the energy of the hydrogen atom. $E_{n} = \frac{{− R}_{H}}{n^{2}}$ This formulation is completely different from that of Bohr, seen above, yet the constant R_H turned out to be exactly the same as the one obtained by Bohr. As before, the value for R_H = 1312 kJ/mol for hydrogen atom.

Angular Momentum Quantum Number, l

Shape of orbital is determined by anuglar momentum quantum number, l. Orbital is related to the probability of finding an electron. If one squares the orbital, it becomes probability.

The value of l runs from 0 to n - 1. So, if you start with n = 2, l can run from 0 to 1. If n = 5, then l can be 0, 1, 2, 3, or 4.

These different orbitals have different shapes. We'll look at them in the next section.

Magnetic Quantum Number, m_l

Degeneracies in the angular momentum quantum numbers —meaning that how many of the same orbital in the given l quantum number.

There are (l - 1)*2 sets of orbitals in a given l, and the value of m_l runs from -l to +l in itegral manner.

So,

m_l

This quantum number came about because the atomic spectra split when the atom is in magnetic field. This splitting occurs due to the negatively charged electron moving around the nucleus. The magnetic field is created when there is a moving charge. (Look at induction of magnetic field by current in the wire, here. Video is not a very good quality, but very informative.)

Spin Quantum Number, m_s

This spin quantum number only assumes either +½ or -½. The +½ electron is called α (alpha) electron, and the -½ electron is called β (beta) electron, represented as ↿ (half up arrow) and ⇂ (half down arrow), respectively, when used within the orbital energy diagram, as discussed below.

Notations

Using above mentioned quantum numbers, we can find out all possible combination of n, l, m_l and are listed in Table 5.1 below.

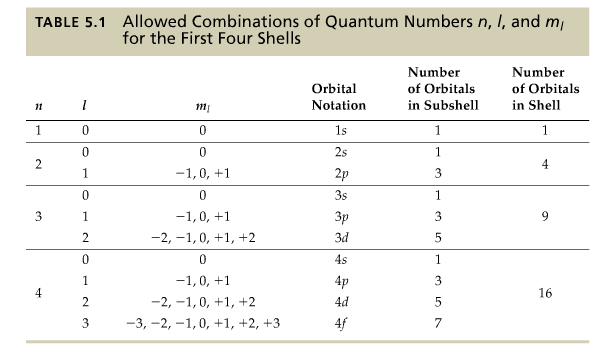
If n = 1, only s orbital is possible, and the orbital arising from the n and l, we call it 1s orbital, etc, as shown in the table.

As it is seen, all p orbitals have 3 sets of orbitals, all d orbtials 5 sets, all f orbitals 7 sets.

Energies of orbitals are shown in the following figure.

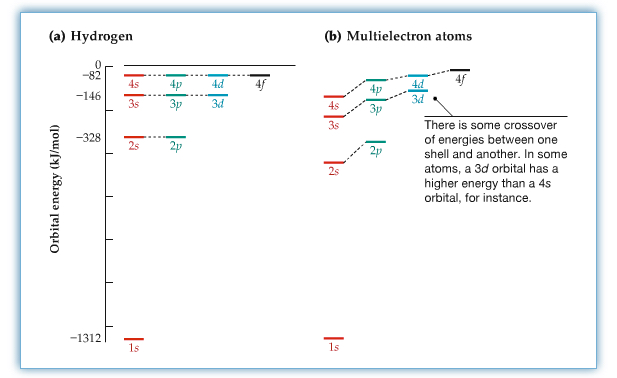
For hydrogen atom the energy of the orbital within the same principal quantum numbers are the same, while multi-electron case are different, due to electron-electron interactions in the atom.

Shapes of Orbitals

What orital represents is where the electrons are found. Each orbital can hold either 0, 1 or 2 electrons. So, for any s orbital can hold up to two electrons, but any p orbitals can hold up to 6 electrons since there are three sets of p orbitals due to the values of m_l (-1, 0, and +1). Therefore, d orbitals → 10 electrons maximum since m_l = -2, -1, 0, 1, 2.

Shapes of orbitals are depended upon the value of l quantum number.

s orbitals for l = 0 — spherical

p orbitals for l = 1

d orbitals for l = 2

f orbitals for l = 3

The following beautiful pictures of orbitals show the shapes of each and the shell structure is clearly shown. The picture is laid out according to the Periodic Table of Elements.

Electron Spin and the Pauli Exclusion Principle

As mentioned above, there are half-integral quantum number, called spin quantum number, m_s. This quantum number also describe about magnetic field of electron. However, this has nothing to do with motion of electron around nucleus. Electron seems to behave as ultimately tiny magnet. The two quantum numbers, ±½, can be thought of as N---S and S---N configurations of a magnet.

In 1925, after very careful sorting of elements of on the Periodic Table, Pauli realized that all 4 sets of quantum numbers, n, l, m_l, and m_s must be different for each of the electrons in an atom. This is called Pauli exclusion principle.

Another way to put this principle, is that there are no more than 2 electron can be placed in an orbital. Therefore, 1s orbital can have maximum of 2 electrons, 2p—6 electrons, 3d—10 electrons.

Orbital Energies in Multielectron Atoms

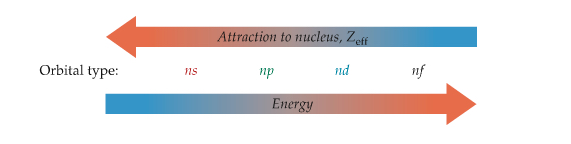
As shown in the Wave Function and Quantum Number section , the orbital energies of multielectron atoms are different from that of the hydrogen atom. This is due to the fact that electron in the low-energy orbitals shields outer electrons. If outer electron is shielded, the attraction to nucleus from the outer electron is effectively less (you can call it effective nuclear charge). The effectiveness of shielding depends on the types of orbitals according to the following figure.

Electron Configurations of Multielectron Atoms

Atoms in ambient temperature and pressure are assumed to be in its lowest energy state, called ground state. When external source such as light or heat is given to atoms, atoms may go to what is known as excited state. Excited state has finite life time, and eventually go down to its ground state. Here we look at how the ground state of atoms is like by placinig electrons into orbitals.

Electron Configuration—how electrons are placed in atomic orbitals. For example, 6-electron atom, carbon is written as

1s²2s²2p² . The superscript tells you how many electrons there are in the specified orbital. In this case there are two electrons in 1s orbital and two electrons in 2s, and two electrons in 2p orbital. How do you know what order to fill?

Use Aufbau Principle. Given the principal quantum number, you can write all possible angular momentum terms, as follows. If n = 1, then orbital arising from it is 1s. If n = 2, then orbitals arising from it are 1s, 2s, and 2p. If n = 3, then orbitals arising from it are 1s, 2s, 2p, 3s, 3p, and 3d. And so on so forth.

Then cross out anti-diagonally, as follows.

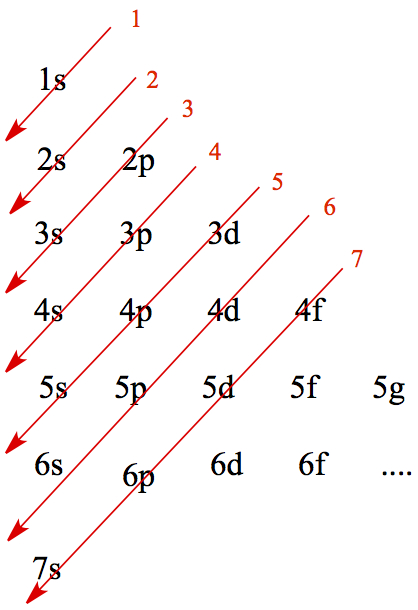
Following the red arrow in order, and write down the orbitals. This is the order to which you fill electrons in multi-electron atoms.

Then, ordering of orbitals are:

1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d...

As you can see for carbon, the electron configuration is s²2s²2p². The superscripted numbers tell how many electrons there are in the orbitals.

Here are some rules you must follow to construct electron configuration:

Lower energy orbitals are filled first.

m_s

Hund's rule

One electron goes into each orbital until all are half-filled.

Using the Aufbau Principle, we can write down most of the electron configuration of elements.

Z	Name	e^- config
1	H	1s¹
2	He	1s²
3	Li	1s²2s¹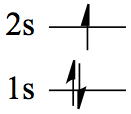
4	Be	1s²2s²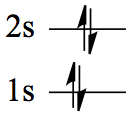
5	B	1s²2s² 2p¹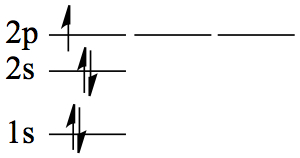
6	C	1s²2s² 2p²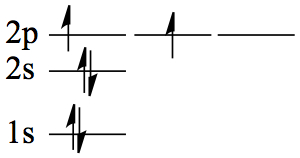
7	N	1s²2s² 2p³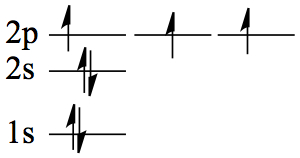
8	O	1s²2s² 2p⁴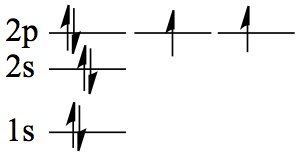
9	F	1s²2s² 2p⁵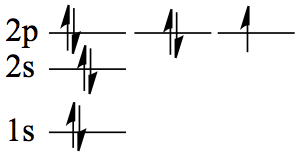
10	Ne	1s²2s² 2p⁶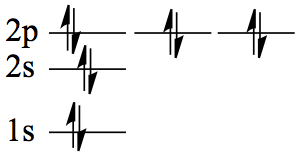
11	Na	1s²2s² 2p⁶3s¹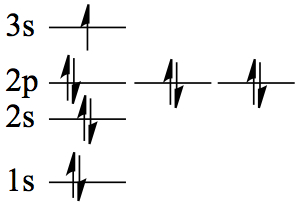

Do you see the pattern? When constructing orbital diagram, don't forget the Hund's rule!

Anomalous Electron Configurations

Even though, the Aufbau principle works great, there are some exceptions that you have to watch out. For example, Cr (z=24) and Cu (z=29). The expected electron configurations of these atoms are:

For Cr, 1s²2s² 2p⁶3s² 3p⁶4s² 3d⁴, but observed one is 1s²2s² 2p⁶3s² 3p⁶4s¹ 3d⁵.

For Cu, 1s²2s² 2p⁶3s² 3p⁶4s² 3d⁹, but observed one is 1s²2s² 2p⁶3s² 3p⁶4s¹ 3d¹⁰

So, as you can see in both cases, s orbital is made into singly occupied, and d into either half-filled or completely filled. The half-filled configuration is more stable than s filled and d unevenly filled.

Here, all anomalous electron configuration species are listed:

Cr, Cu, Mo, Au, Ru, Rh Rg, Pt, Pd, La, Ce, Gd, Ac, Th, Pa, U, Np, Cm, Ds, and Rg.

Electron Configurations and the Periodic Table

Now, we are at the point for which how the periodic table is layed out. It might be quite obvious now. Look at the following figure.

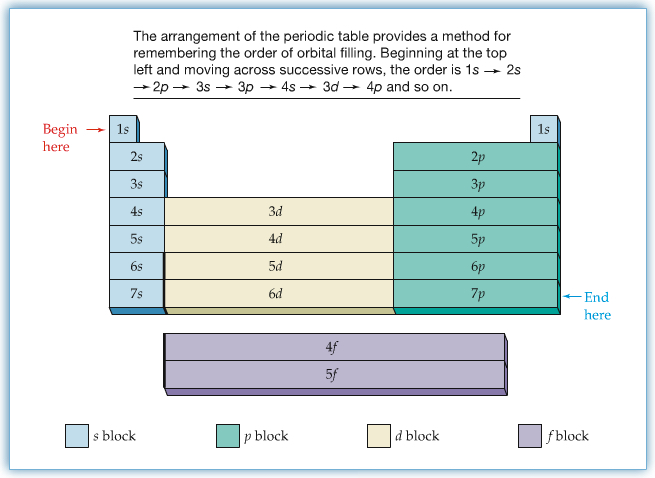
From quantum mechanical point of view, each row represents the principal quantum numbers, and if the element belong to the same group, the highest energy orbitals have the same characters.

Group	Orbitals
1 and 2	s
13 to 18 (or 3A to 8A)	p
3 to 12 (transition metals)	d
Lanthanides and Actinides	f

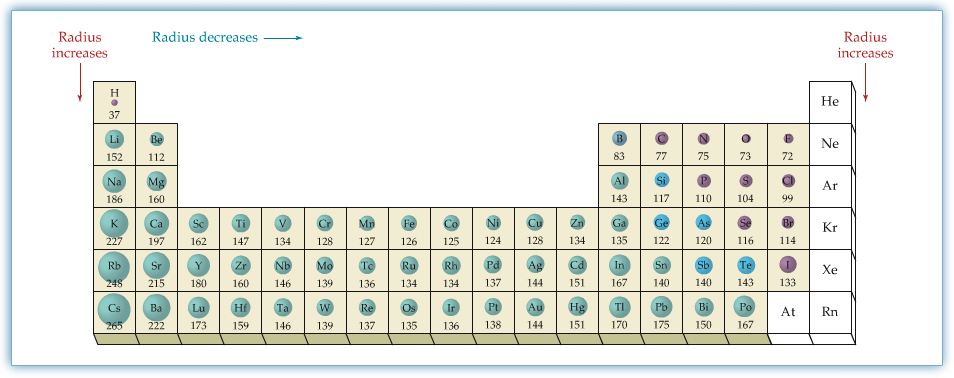
Atomic Radii

Atomic Radius—defined by the half of the distance between two of the same nuclei (homonuclear diatomic molecule).

Hydrogen molecule, H₂, has its bond distance of 0.741 Å. Therefore, hydrogen's atomic radius is 0.375 Å. The following table shows the atomic radii. The values are in pm.

Electron Configurations of Ions

As we have seen in the previous chapter, electron configuration is the key in understanding where atoms are located on the Periodic Table of Elements.

Can we understand how ions are made in terms of electron configuration?

We know that Na atom tends to become +1 ion, and the group 17 atoms tend to become -1 ions.

Group	Charge
1	+1
2	+2
17	-1
16	-2
15	-3

The electron configurations of Na (11 electrons) and Na⁺ (10 electrons) according to aufbau principle are:

Na: 1s²2s²2p⁶3s¹

⁺

⁶

The electron configurations of Cl (17 electrons) and Cl^- (18 electrons) according to aufbau principle are:

Cl: 1s²2s²2p⁶3s²3p⁵

⁶

The point here is that ions are made such that the noble gas configuration is obtained for each. For Na, Na⁺ assumes Ne configuration, and for Cl, Cl^- assumes Ar configuration.

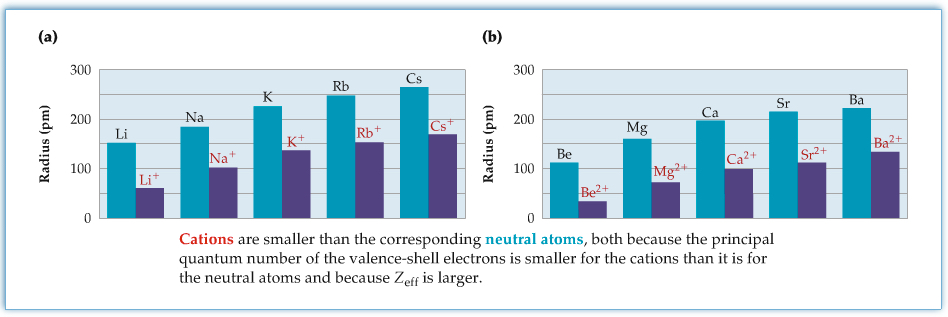
Ionic Radii

Ionic radii of atoms are substantially different from those of neutral atoms. The following two figures show, respectively, ionic radii of cations (groups 1 and 2), and ioinic radii of anions of halides (group 17). The cationic radii are much smaller than the parent neutral atoms, and the ionic radii of anions are much larger than the parent. The effect has to do with the effective nuclear charge that we talked about in Chapter 5. For cation, the valence electrons are less shielded due to the loss of electron such that there are more positive charge effectively. On the other hand, the anion's valence electrons are more shielded due to extra electron.

Ionization Energy

Ionization energy (or ionization potential)—energy required to remove the highest energy electron from atom to make a cation. We denote it as E_i1.

We know from the structure of hydrogen atom that its ionization energy is 1312 kJ/mol (Chapter 5).

Second ionization energy is the energy required to remove the second electron from a cation, denoted as E_i2.

The periodic trend of ionization enery is shown in the following figure.

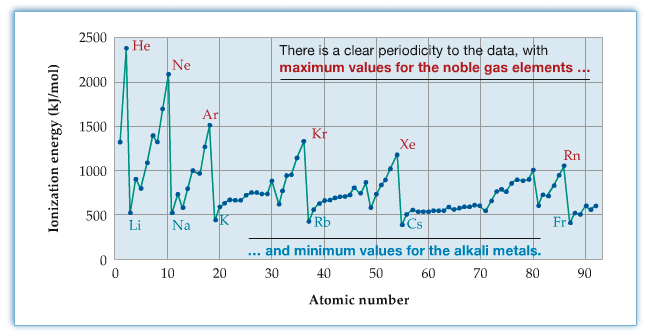
As it is seen above, as one moves toward right side of the Periodic Table, ionization potential increases. For elements in the same group, the ionization energy reduces as one moves down.

Higher-order ionization energy, that is the energy required to remove 2^nd, 3^rd and higher electrons, also has some trend. The following table shows the trend.

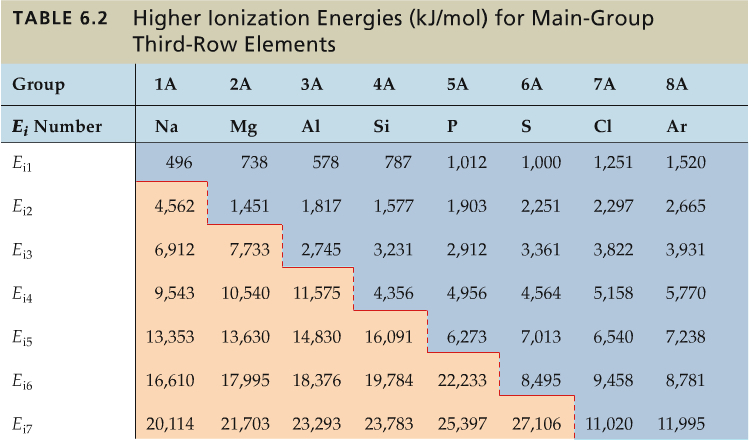
There is a shape dividing line between relatively small ionization energy and very large ones. For Na, after E_i1, the ionization energy sharply rises. For Mg, it is after two electrons. For Al, 3, and so on so forth.

Electron Affinity

Electron affinity—energy released by atom upon receiving an electron.

If the atom such as Cl receives an electron and becomes Cl^-, the resulting anion is more stable by more than 350 kJ/mol! If unstable anion is formed, then we define electron affinity to be 0 kJ/mol. This is due to the fact that experimentally such energy is not measurable.

The following figure shows the periodic trend for electron affinity.

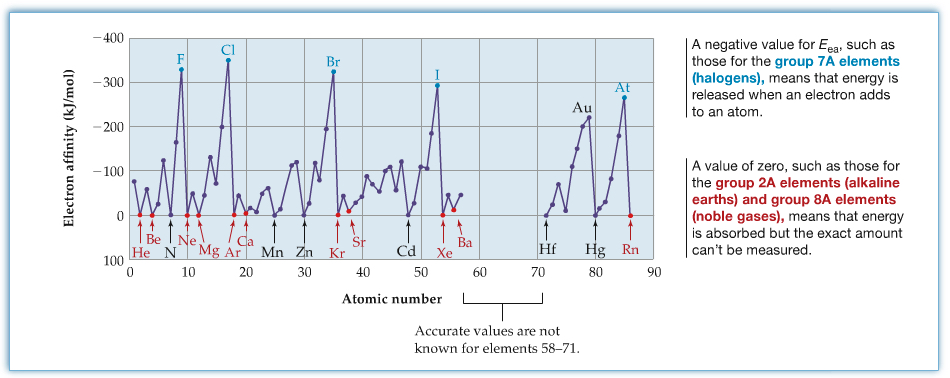
The periodic trend is that, for main group elments, the electron affinity increases as the atomic number, Z, increases. However, as you can see in the figure, nitrogen and phosphorus have the decreased of electron affinity. This is due to the stability of these atoms for their electron configurations being half-filled with the p³ configuration. You see the similar trend in Mn where the electron configuration is ...4s²3d⁵.

Octet Rule

From what we have seen on the periodic trend is that:

^st

_i2

Group 17 elements have the large electron affinity — therefore more stable

Group 18 elements have the largest ionization energies, and zero electron affinity — both tell stability is hight in these elements

All of the above facts shows the stability of noble gas electron configurations in the main group elemetns.

Octet Rule:
So, whenever possible, the main group atoms tend to surround themselves with eight electrons to become the noble gas electron configuration.

Example: The following ions all have the same umber of electrons: Ti⁴⁺, Sc³⁺, Ca²⁺, and S^2-. Order them according to their expected sizes, and explain your answer.

All the ions have 18 electrons, therefore, they are like Ar. For Ca, Sc, and Ti ions, the ionic charge increases, and it means that electrons feel more attraction to the positive charges. Therefore, among the three, from small to large, you have Ti⁴⁺ < Sc³⁺ < Ca²⁺.

The atomic radius of S is listed as 104pm in the figure above for the atomic radii. Comparing this number with the ionic radius of the cations shown above Ca²⁺ ion is about 100pm. Therefore, the negative ion of S should be a lot larger than its neutral atom. Thus, the ordering of size must then be:

Ti⁴⁺ < Sc³⁺ < Ca²⁺ < S^2-

Lattice Energy

Lattice energy is the stability (in + value) of formation of ionic compound from the constituent ions in gas phase. For example, in the case of the LiF(s), the lattice energy is given by chemical equation,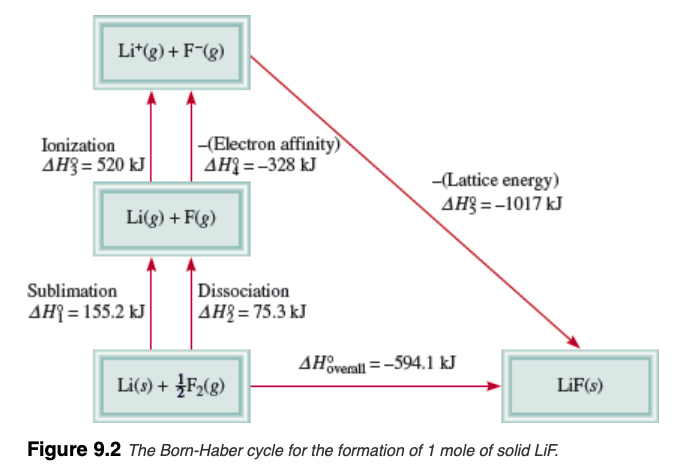 Li⁺(g) + F^-(g) → LiF(s) ΔH_lattice = -ΔH_rxn However, generally what we obtain experimentally is not the equation above. For LiF, the chemical equation is, Li(s) + ½F₂(g) → LiF(s) By knowing Hess's law and several of the ideas discussed in Chapter 8, we can construct the energy diagram to understand how one can obtain the lattice energy.

This type of representing the energetics is called the Born-Haber cycle.

Covalent Bond

When molecules are made, chemical bonds formed between different nuclei. The chemical bonds formed are so-called, covalent bonds. A covalent bond is formed between two nuclei so that resulting molecule is stabilizized, hence existence of the molecule.

The interactions of particles in H₂ molecule for example is only electromagnetic in nature, more specifically Coulomb interactions. As shown below, even a simple molecule such as H₂ has this many interactions to be taken into account, although they are all Coulombic in nature,

$V = c \frac{e_{i} e_{j}}{r_{ij}}$ where V is the interaction energy between two charged particles, e_i and e_j, r_ij is the distance between the charged particles i and j, and c is the proportionality constant. If the two charges are the same V > 0, which means that the interaction is repulsive. On the other hand, the two charges are different, V < 0, which means that the interaction is attractive. In H₂, we have these interactions:

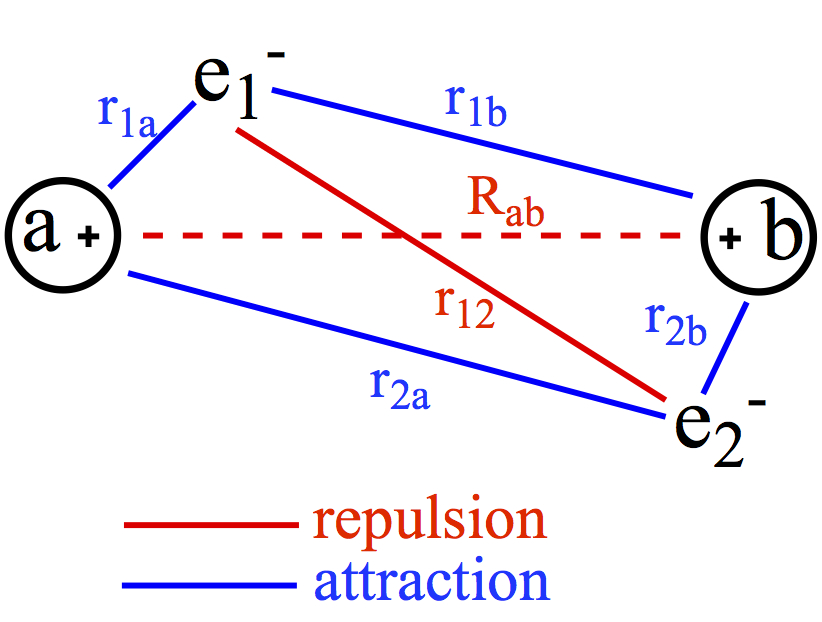
The red lines are repulsive interactions, and the blue lines represent attractive interaction. As simple as it seems, in H₂ molecule has six interactions to worry about. When we put these interactions in Schrödinger equation, we obtain the quantum mechanical description of chemical bond.

Remember from the previous chapters that Schrödinger's theory is wave mechanics. So in order for two H atoms to form a chemical bond, two waves one from each H atom collide. The figure below shows what happens when the two hydrogen atoms collide. Notice the tails of the two wave functions overlapping.

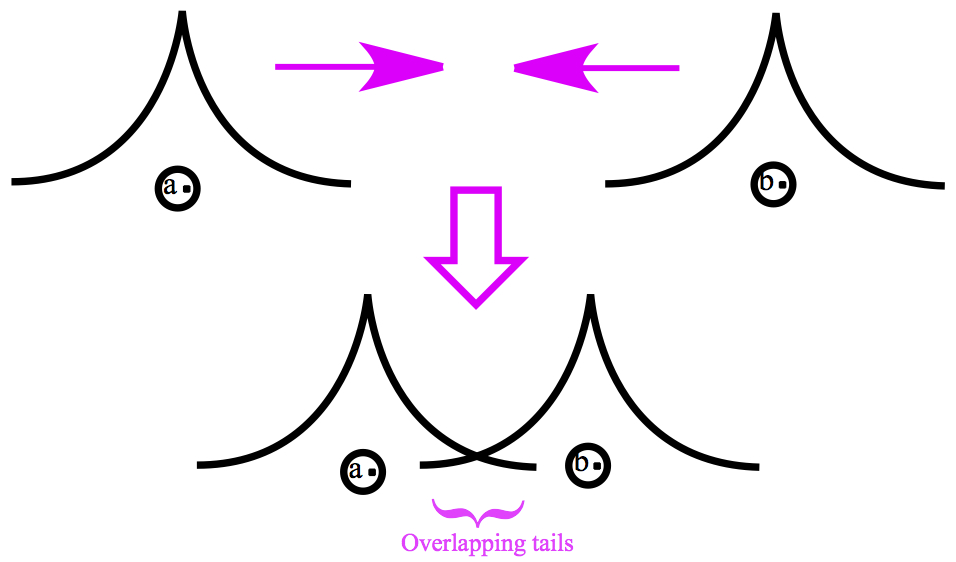
Afterall, these are waves. When, for example, two waves on water collide, the resulting wave shows interference pattern. Similarly, interference does occur in quantum mechanics, as well. Two types of interference: 1) constructive and 2)destructive. Constructive interference in H₂ makes a bonding orbital, and destructive interference results in the so-called anti-bonding orbitals. (More on this later.) Basically, the bonding characteristic of covalent bond came from the interferences of two colliding wave functions.

As far as energy is concerned, when chemical bond forms, the molecule is stabilized. The stability of molecule, as compared to two separated atoms, tells that the energy is released when chemical bond forms. On the other hand, when you want a chemical bond to break, you need to inject energy into the bond. The relationship between energy of molecule and the bond distance between two nuclei is shown in the figure below.

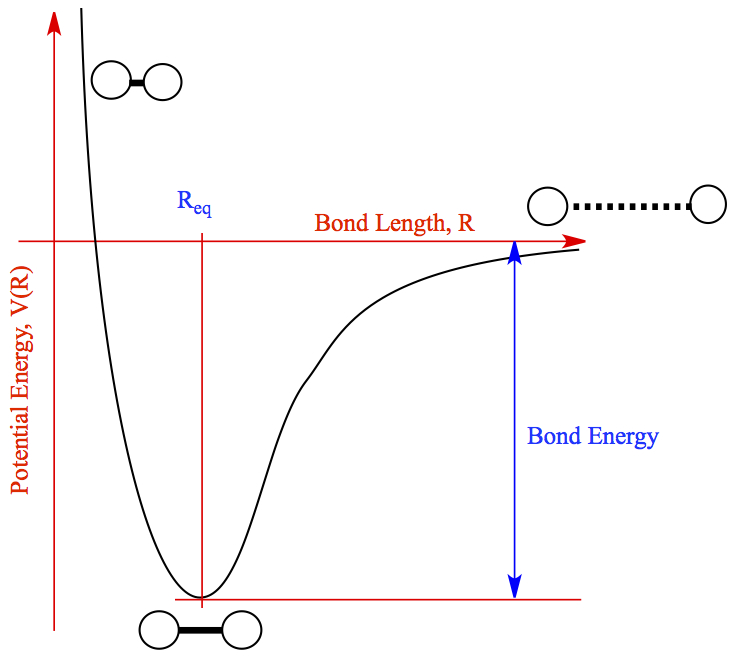
The general shape of the energy of any molecule as a function of bond distance looks like the above; different bonds have the different bond energy and the location of the equilibrium bond distance, R_eq, shown at the bottom of the well in the figure. The equilibrim bond distance is what we generally refer to as bond length or "bond distance".

So, from R_eq and try to break a covalent bond, you need to add energy to the system, while from two separated atoms to form a bond, there would be an energy release.

Strength of Covalent Bonds

It is possible for a molecule to have more than one covalent bond between the same nuclei. We generally refer to them as multiple bonds. If there are two, it is said that there is a double bond, triple bond for three, and so forth. For example, nitrogen molecule, N₂, has a triple bond.

So, as shown in the figure above (energy of molecule as a fxn of bond distance), one needs to put energy into the molecule to break a chemical bond. If there is more than one bond between the two nuclei, it stands to reason that there are more energy needed to break the multiple bond. Here, some examples are presented.

# of bonds	CC	NN	CO
Single	350	240	350
Double	611	418	732
Triple	835	945

Polar Covalent Bonds: Electronegativity

When a chemical bond is formed, the electrons feel their environment. If the bond formation dealt between Na and Cl, due to Na's low ionization energy and Cl's high electron affinity, Cl grabs an electron from Na's valence shell to form Cl^- ion and Na becomes Na⁺. In this case, the bonding is ionic. In the case of two carbon atoms, the resulting chemical bond is covalent in nature, and since both nuclei are C, the two C atoms share the two electron equally. However, there are many many molecules that their situations are in between NaCl and -CC- bondings. We refer to covalent bonding between the two extremes as polar covalent bond. A figure below shows the situation.

In the figure above, δ indicate a partial charge of atom in the molecule. The δ+ indicates that the atom has partiall positive charge, and the δ- indicates that the atom has partial negative charge. Even in a NaCl molecule, the overall charge of the molecule is zero, however, because of high electron affinity of Cl and the low ionization energy of Na, Cl gets - nad Na gets +. Similarly, in molecule in general has partial charges on atoms involved in bonding. One way to understand the polarity in covalent bonds, electronegativity can be used to assign partial charges on atoms. There are periodic trends in elelctronegativity, as shown in the figure below.

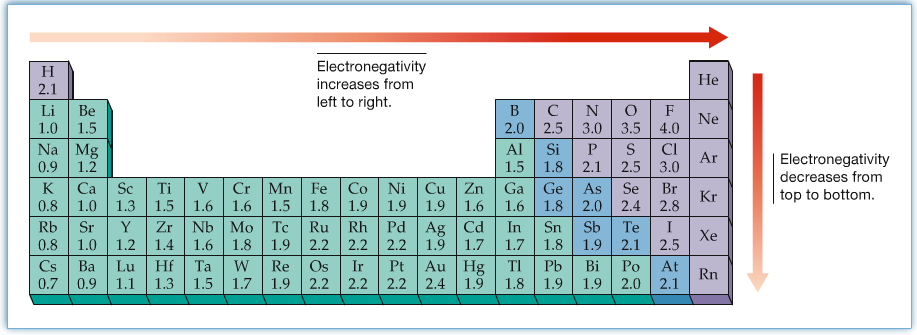
One can define electronegativity to be the ability of atom in a molecule to attract the shared electrons in a covalent bond. The highest electronegativity is assigned for fluorine, and the value of electronegativity decreases as going down the row in the periodic table, as well as going toward the left-side of the table.

electronegativity difference

One of the consequences of having a polar bond in a molecule is that, among other things, it can predict reactivity of molecules, particularly in organic chemistry that you take next year!

Electron-Dot Structures, Lewis Dot Structures

Covalent bond is to share two electrons between two nuclei. So, one can draw H₂ molecule as the following.

H : H

The two dots in the middle indicate that two H's share two electrons. This is called electron-dot structure or more generally known as Lewis (dot) structure.

In order for us to draw a Lewis structure for a given formula, one must know the number of valence electrons. For the main group elements and hydrogen, we have:

Group	# valence e^-	# of bonds
13	3	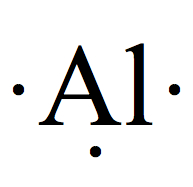3
14	4	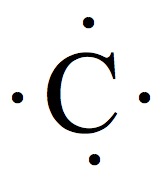4
15	5	3
16	6	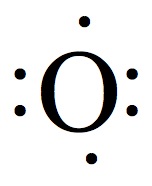2
17	7	1
H	1	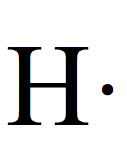1

We now utilize the octet rule we learned in Chapter 6 to draw a Lewis structure. Let's use water as an example. For H₂O, if we do the following all electrons are paired, and more importantly, oxgen atom satisfies octet.

If we place the oxygen atom in the middle and two hydrogens on the side, you can connect two dots that are not paired (red lines). The line represents the covalent bond. Then, oxygen now satisfies octet, having 8 electrons around it.

You notice that the resulting water structure has two pairs electrons, these pairs of electrons are called lone pair. The lone pair electrons in general don't usually react to form a bond to another atom.

So, drawing a Lewis structure basically boils down to connecting two dots.

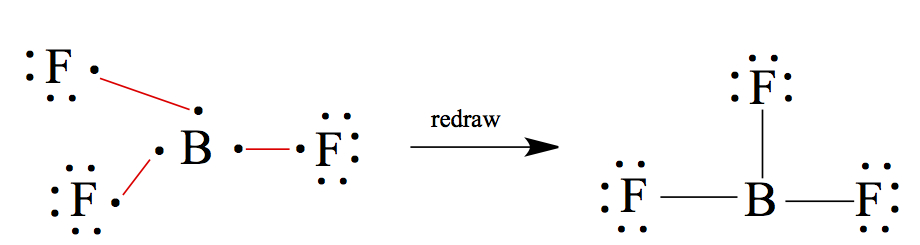
Example: Draw Lewis structures for the following molecules, BF₃, NO, CO, CO₂, and H₂O₂.

BF₃: B is group 13, therefore 3 valence electrons, and F is group 17, thus 7 electrons. B should be the central atom.

NO: N has 5 valence electrons and O has 6. So, connect two sets of unpaired electrons.

You notice here that one of the unpaired electron for N doesn't have a partner. For this molecule, this is as much as we can, so leave it. The unpaired electron left in a molecule is called free radical, highly reactive molecules.

CO: Similar to above, but quite difficult case. Using what we have done, that results in the middle case, where we have a double bond. There are two other structures we can draw, without violating the octet rule.

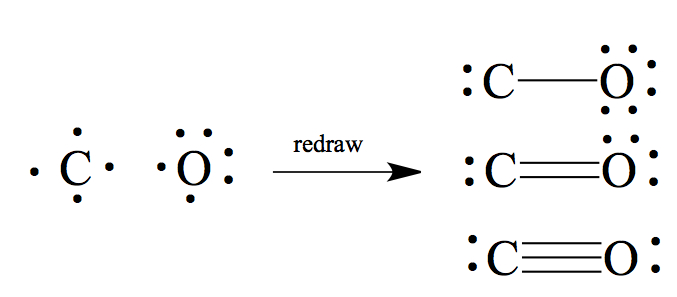
The actual winner is the triple bonded molecule. Generally, C-O single bond is about 1.43Å, and C=O double bond is 1.23Å. Carbon monoxide bond is much shorter, with 1.13Å, and therefore we must conclude that there must be a triple bond to be consistent with the bond length.

CO₂: If you have more than two atoms, less electronegative element becomes the central atom, except for H. In this case, C should be in the center.

H₂O₂:

For ions

The following examples show how you might go about constructing ionic structures.

In the first frame, draw all atoms with their valence electrons

2^nd frame. Connect unpaired electrons

3^rd frame. Keep in mind that you have one extra electron. Move the electron on the bracket to complete the octet on one of the oxygen

Last frame. Redraw.

Similar procedure, but keep in mind that there are two extra electrons

Once in a while, you encounter a situation that simply drawing a bond between two dots does not work. The case in point is HNO₃.

1^st frame. As usual, draw atoms with their valence electrons.

2^nd frame. Connect atoms with bonds.

3^rd frame. Two lower oxgens still have un paired electrons. One of the oxgen unpaired electron is bonded to one of the lone-pair electrons on the nitrogen to form a double bond. The broken lone-pair electron can be transferred to the unpaired electron on the oxygen on the right, you can make a new lone-pair.

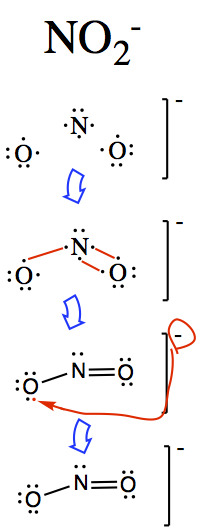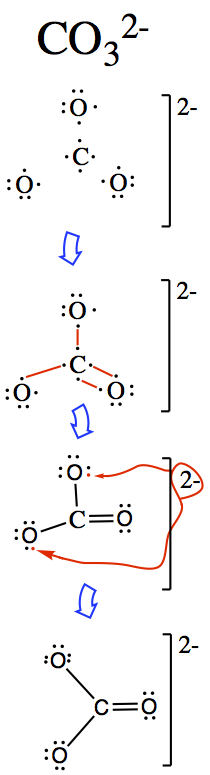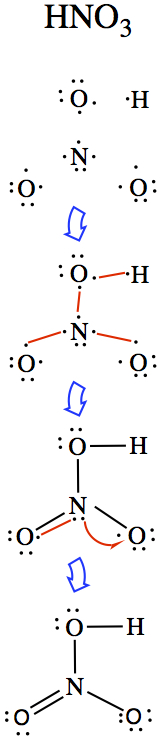Temptation is to do the following:

This results in 5 bonded nitrogen which has 10 electrons around it, hence it is no longer satisfying octet.

Last frame. Redraw.

For larger molecules

There are many different structures one can draw for a given formula. For example, C₃H₄O, I found seven different structures, called structural isomers, as shown below.

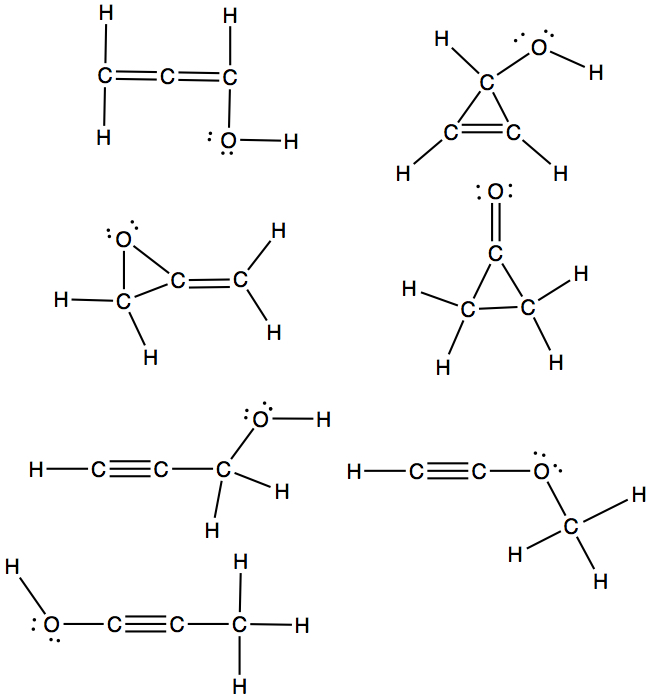
If the formula is C₃H₆O, then there are 7 (could be more) isomers!! These are all application of connecting dots, and they all satisfy octet!

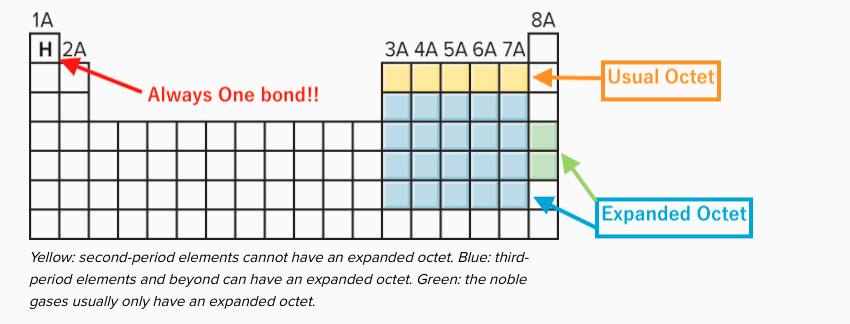
For molecules containing 3^rd row elements and beyond

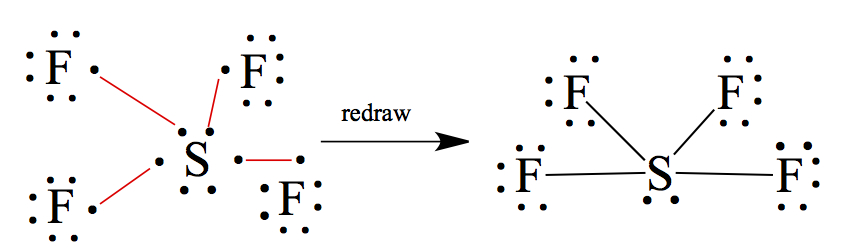
It is possible for 3^rd row elements and heavier elements to have more than 8 electrons around the central atom. We call this expanded octet. For example, the structure of SF₄ is shown below.

Around the central S atom there are 10 electrons. So, S is said to have expanded octet.

The following diagram will help you determine if the expanded octet should be used in the Lewis structures you might draw.

Note: Hydrogen can only form one bond!!!!

Resonance Structures

In the case of carbon monoxide structures we examined above, we said that between C and O there should be a triple bond, justifying our structure through experimental bond distance.

Just by following the usual way of drawing Lewis structure, you should have arrived at the middle picture with a double bond. The two other structures can be deduced by writing resonance structures from the double bonded structure.

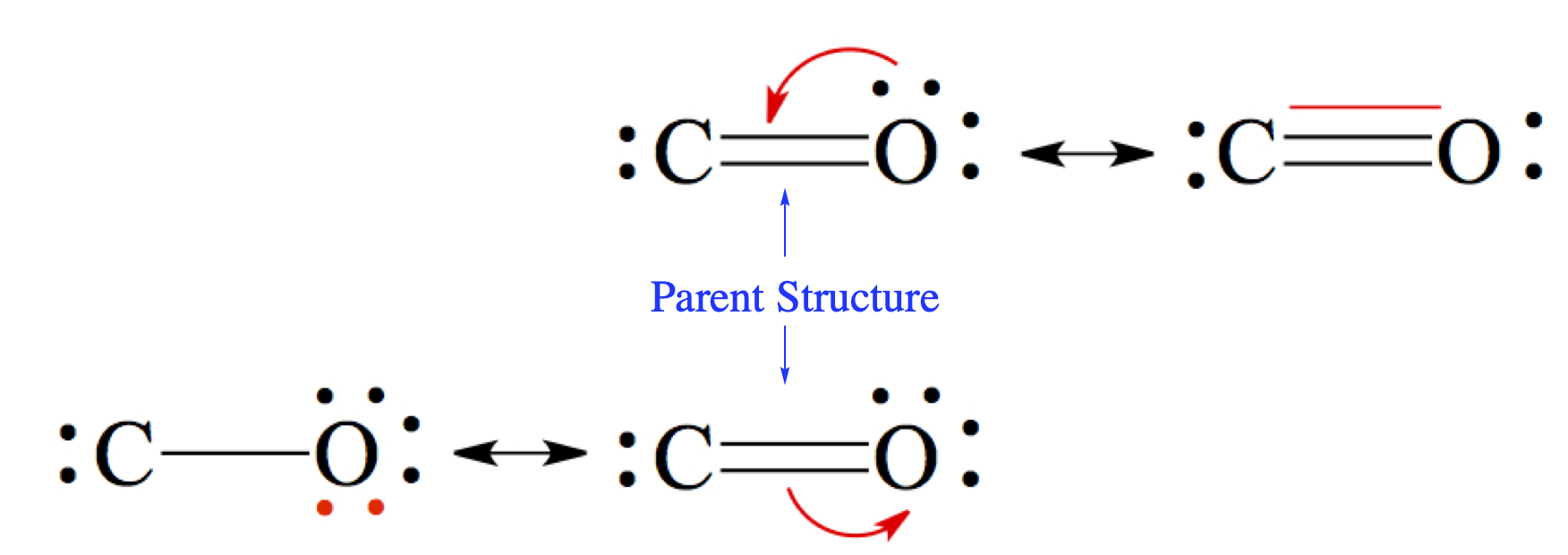
The double-sided arrow, ↔, in chemistry is reserved for resonance structures. The resonance structure with triple bond is constructed by taking one of the lone pair of oxygen and make the pair into a bond between C and O. You notice that there is no violation of the octet rule here. The bottom-left structure is make by moving a pair of electrons from the double bond to the oxygen. Here again, there is no violation of the octet rule. For the C atom, there are only four electrons, this makes C to have + charge and O to have - charge. In the triple-bonded molecule, the C atom has - charge, while O has +. See more in the next section.

Two resonance structures are related by moving electron pair such that

1) the resulting structure has the same number of valence electrons as the parent molecule,
2) Octet rule is followed, except that trivalent Carbon atom may have the formal charge of -1 and +1, and
3) the positions of nuclei do not move.

Another example applied to C₅H₇⁺ ion.

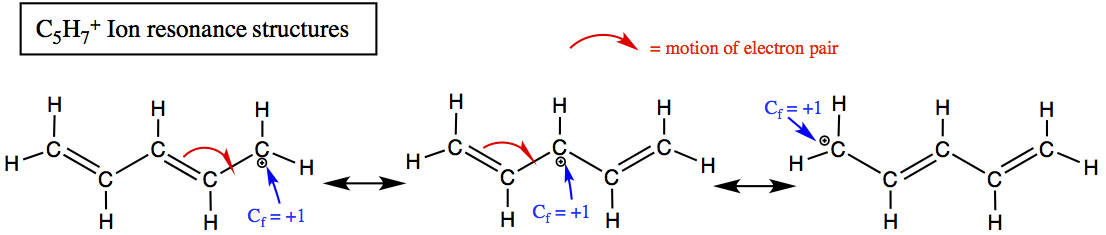
See how the + charge moves within the three resonance structures?

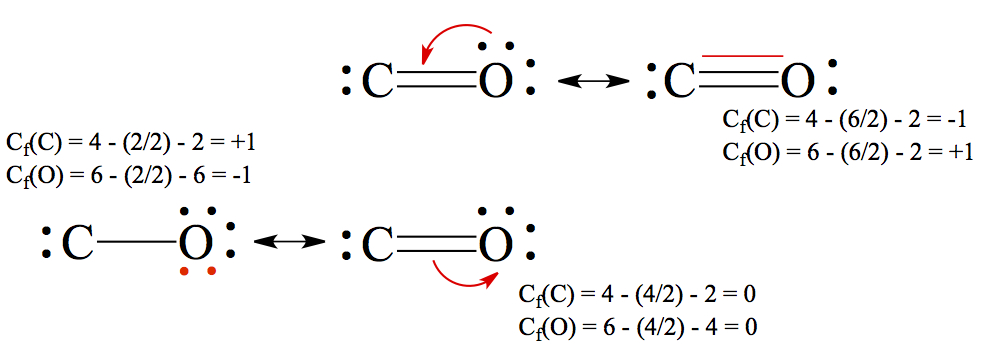
Formal Charges

Again, I'd like to bring up the carbon monoxide example. We had single-bonded, double-bonded, and triple-bonded CO, and I made an excuse of having to compare the bond distance to say that the triply bonded CO is perhaps the best resonance structure. Often times, formal charge on the atoms in a molecule is calculated to differentiate the stability of particular isomer.

Formal charge, C_f, is a fictitious charge of atoms in a molecule. One can calculate formal charge by using the following equation.

C_f = n_ve - n_be/2 - n_nb

where n_ve, n_be, and n_nb are the number of valence electros, number of bonded electrons, and number of non-bonding electrons, respectively.

Using the carbon monoxide example, we calculate the formal charges of C and O for each of the resonance structure.

Example: Draw all resonance structures of an OCN^- ion in O-C-N configuration. Assess which structure is most stable.

These are the structures drawn for the O-C-N configuration.

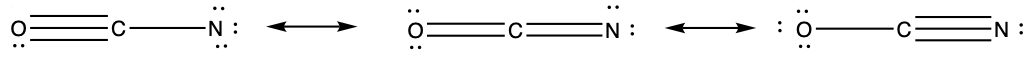
In order to obtain the stability of the ions, one can calculate the formal charges for each atom in the ions. Since all C has four bonds, which means that C_f(C) = 4 - 8/2 -0 = 0. So, calculate C_f for O and N.

+ Formal charges to check the stability among resonance structures.

Therefore, most stable one should be the struture on the right, and the least stable one is on the left.

We can assess the stability of molecule by calculating the formal charges of atoms in the molecule, having more than one resonance structure.

This concept is important in Organic Chemistry!

Bond Enthalpy

Bond Enthalpy, BE, is enthalpy change associated with breaking a chemical bond. Thus, BE always has a positive value.

Remember that

Breaking a bond == endothermic process

Making a bond == exothermic process

For example:

HCl(g) → H(g) + Cl(g) ΔH^° = 431.9 kJ/mol Then, by using one of the thermodynamic rules, you get H(g) + Cl(g) → HCl(g) ΔH^° = -431.9 kJ/mol

One can apply this idea of bond breaking and bond making in approximating the enthalpy change of reaction. After all, reaction is nothing more than bond breaking and bond forming.

Then, the entire reaction can be viewed as a sum of bond breaking (mainly in reactants) and a sum of bond making (mainly in products).

ΔH_rxn = ∑ n_b [BE(bond broken)] - ∑ n_f [BE(bond formed)] where ∑ signifies the sum over all bonds broken and formed, and n_b = the number of moles of bonds broken, and n_f = the number of moles of the bonds formed.

For example, the enthalpy change of the reaction,

CH₄ + HCl → CH₃Cl + H₂ is given by one of the C-H bond broken (BE(C-H) = 414 kJ/mol) in CH₄, by the H-Cl bond broken (BE(H-Cl) = 432 kJ/mol), by the formation of C-Cl bond (BE(C-Cl) = 338 kJ/mol) and H-H bond formation (BE(H-H) = 436 kJ/mol). Thus, we have
ΔH = BE(C-H) + BE(H-Cl) - BE(C-Cl) - BE(H-H) ΔH = 414 kJ/mol + 432 kJ/mol - 338 kJ/mol - 436 kJ/mol = + 72 kJ/mol. Thus, the reaction is approximately endothermic by 72 kJ/mol.

Valence Shell Electron Pair Repulsion Theory

3-D structures of Molecules We now now how to draw a structure of a molecule in 2-D by using connecting unpaired electrons.

Molecules in reality is not two-dimensional. They are actually three-dimensional entity, and have trend to assume certain shapes. In this section we use Valence Shell Electron Pair Repulsion (VSEPR) theory to deduce 3-D structure of molecules. 3-D structure is extremely important, since in many instances, reactivity of molecules can be determined.

From the Coulomb's law, the first equation at the very top of this page, the charges of the same sign have repulsive interaction. Considering the fact that molecules are made of chemical bonds and some have lone pair electrons, there must be bond-bond repulsive interaction or bond-lone pair interaction. The VSEPR theory utilize these repulsive interactions to deduce the 3-D structures of molecules. They key is to minimize the repulsive interactions in a molecule.

VSEPR Theory We must count and classify the number of charge clouds in order to deduce three-dimensional structure.

# of Bonds

# of Lone Pairs

Total # of Charge Cloud

# of bonds

# of lone pairs

By using the following table, one can deduce the 3-D structure.

Charge Clouds	# of Bonds	# of Lone Pairs	Structure	Example
2	2	0	Linear	CO₂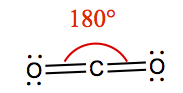

3	3	0	Trigonal Planar	COH₂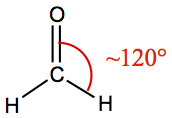
3	2	1	Bent	SO₂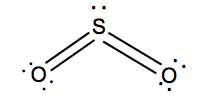

4	4	0	Tetrahedron	CH₄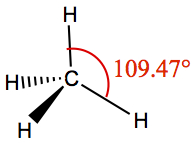
	3	1	Trigonal Pyramid	NH₃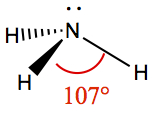
	2	2	Bent	H₂O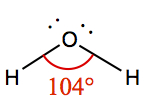

5	5	0	Trigonal Bipyramidal	PF₅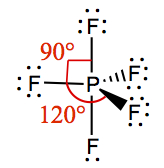
	4	1	See-Saw	SF₄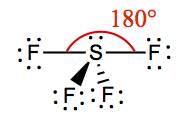
	3	2	T-shaped	ClF₃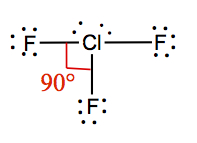
	2	3	Linear	XeF₂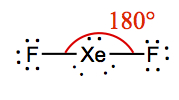

6	6	0	Octahedral	SF₆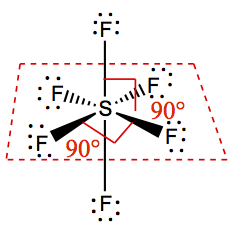
	5	1	Square Pyramidal	ClF₅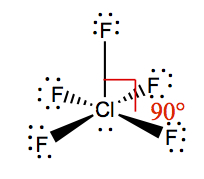
	2	2	Square Planar	XeF₄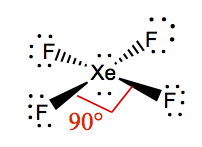

In order for you to determine the 3-D structure, you must first be able to draw a Lewis structure of the molecule so that the number of charge clouds, the number of bonds, and the number of lone pairs are known.

Dipole Moments

We learned above that many bonds are polar bond, determined by electronegativity difference between two atoms. When all bond polarities are added to obtain total polarity, we get dipole moment of molecule.

Remember that Fluorine is has the highest value of electronegativity, χ? Due to electronegativity difference, Δχ, b/w two atoms, bond would polarize.

If the Δχ = 0, then the bond is said to be non-polar.
If the Δχ is non-zero, the bond is polar.

So for molecule N=O, we have
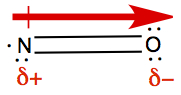As it is seen, arrow indicates the dipole moment of the bonds between N and O, and the arrow points toward more negative side, indicated with δ-, and the other end is more positive side, δ+. This is so because oxygen is closer to F in the periodic table than nitrogen.

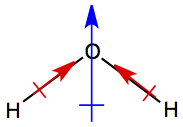Adding all Polarities of bonds → molecular dipole moment, μ

The bond dipole moments of O-H bonds (red arrow) in water points toward oxygen atom. When these two bond dipoles are added together, molecular dipole moment (blue arrow) is produced. As in the bond dipole, the direction the arrow is pointing has partially negative charge, and the opposite end has partially positive charge.

Example: Draw in polar bonds with arrows to show the bond dipole moments and molecular dipole moment of dimethyl ether (CH₃O CH₃), tetrafluoromethane (CF₄) and HCOCH₂CF₃.

In order to deduce dipole moments of molecule is to know the 3-D structure of the molecule. Then, draw in the bond dipoles (red arrows). We consider C-H and C-C bonds to be non-polar bonds, therefore we don't draw in the arrow for these bonds. After bond dipoles are drawn in, all bond dipole vectors are added, and the resulting vector is the molecular dipole moment (blue arrow ).

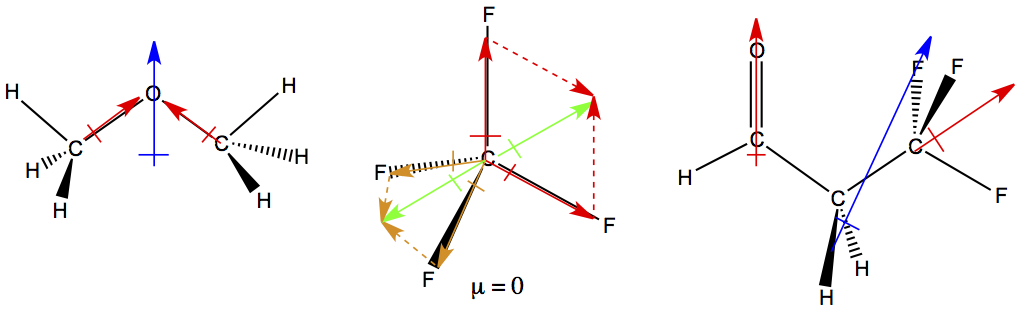
For CF₄, two of the red bond dipoles form a resultant green dipole in the plane of the computer monitor. For other two bond dipoles, with orange color, form another green resultant pointing in the opposite direction. And, they cancel each other, therefore the moleuclar dipole moment of CF₄ is zero.

Bond dipole is a Very Important Concept!! You'd have easier time knowing bond dipole and moleucular dipole moments in organic chemistry, Yes, in organic chemistry!

Valence Bond Theory and Hybrid Orbitals

When drawing a Lewis structure, we used a pair of valence electrons from each nucleus in the molecule to form a chemical bond.

We also talked about formation of chemical bond in H₂ from two hydrogen atoms; two 1s orbitals approach each other with overlapping tails, which gave rise to bonding and antibonding orbitals.

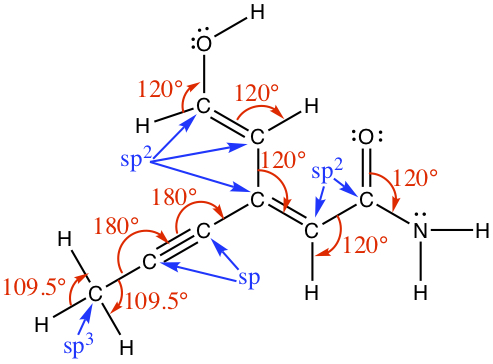
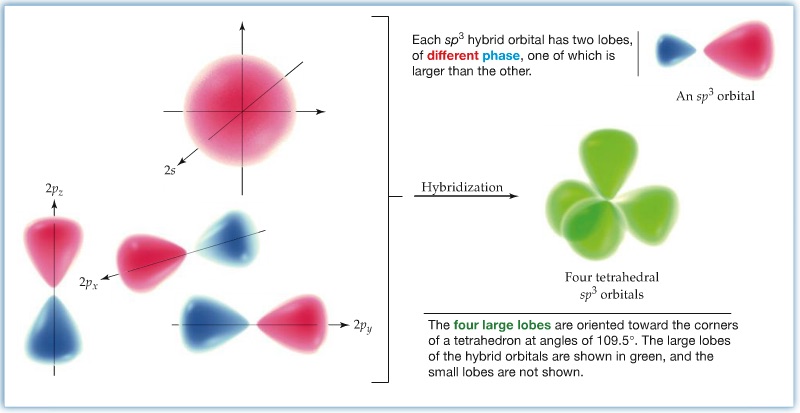
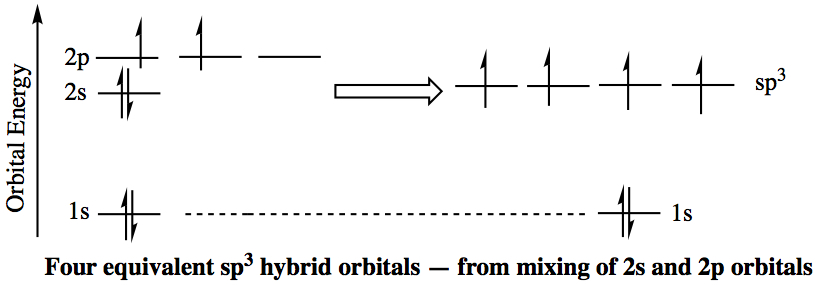
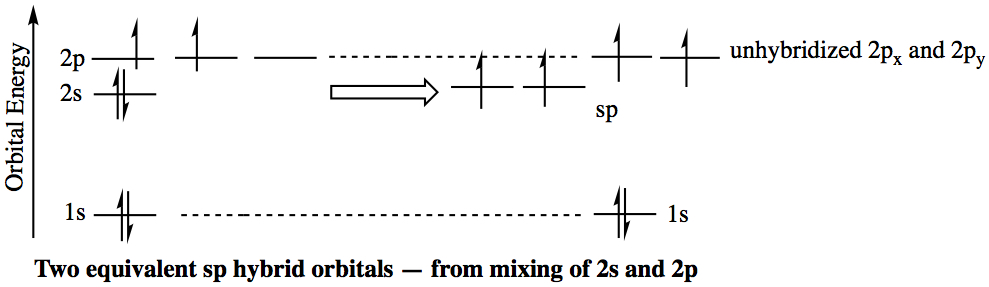
sp³ Hybrid Orbitals: Upon forming a chemical bond, for example in CH₄ 1s orbitals of four hydrogens overlap with the carbon's 2s and 2p orbitals, because carbon's valency is 4. Since methane assumes tetrahedral structure, each of the four bonds has to be completely equivalent. This means that carbon's atomic orbitals have to be modify to accomodate the four hydrogens' 1s orbitals. The accomodation comes via forming a so-called, hybrid orbitals. Carbon needs to use four of orbitals (2s, 2p_x, 2p_y, and 2p_z) and the four orbitals mixes to obtain four equivalent atomic orbitals, known as sp³ hybrid orbitals, as shown below. The sp³ orbital overlaps with hydrogen's 1s orbital to form a covalent bond, called σ bond.

The angle between each lobe assumes 109.47° since the sp³ carbon is tetrahedral.

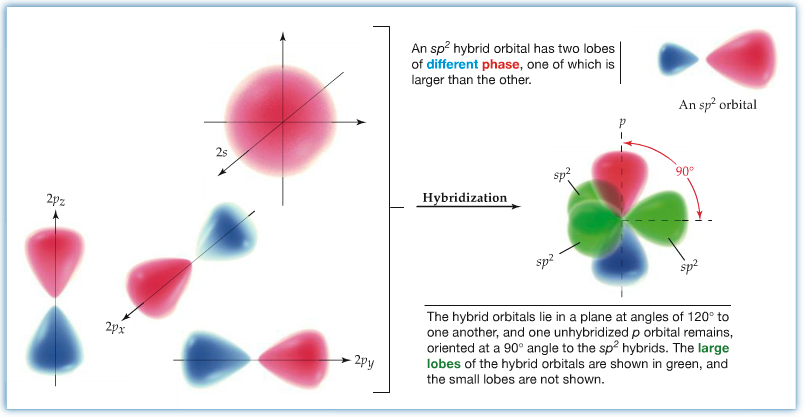
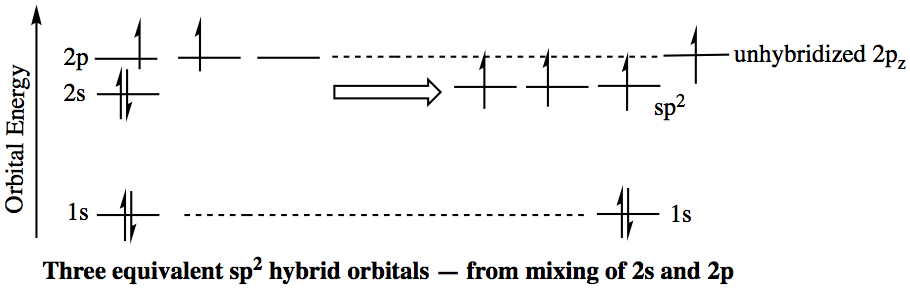
In terms of orbital energy diagram, it is shown below the how hybridization takes place.

sp² Hybrid Orbitals: If a carbon atom is in a double-bond environment, such as C₂H₄ (ethylene), the carbon is hybridized to become sp² hybrid orbital. As we have seen in the VSEPR theory, double-bonded carbon has a trigonal planar structure with approximate bond angle of 120°. In order to have three σ bond connections, one 2s and two 2p orbitals have to be mixed. This leaves unhybridized 2p orbital. The unhybridized 2p (typically 2p_z orbital) orbital is involved as the second bond to another carbon. We call this a π bond . The bond angle between the lobes of hybridized orbitals are about 120°, and each lobe is coplanar. The unhybridized p orbital is 90° to the plane. The sp² hybrid orbital is shown below.

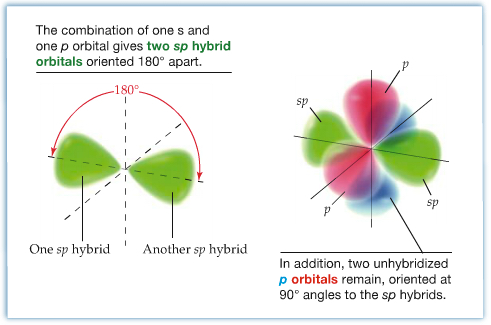
sp Hybrid Orbitals: In this case, a carbon atom is in the triply bonded enviroment. The VSEPR theory predicts that acetylene (C₂H₂) is a linear molecule (180° bond angle). Each carbon is bonded to two other atoms, hence only two atomic orbitals, namely one 2s and one 2p orbital are needed for hybridization. Two other 2p orbitals are unhybridized. These unhybridized p orbitals are involved in two π bonds.

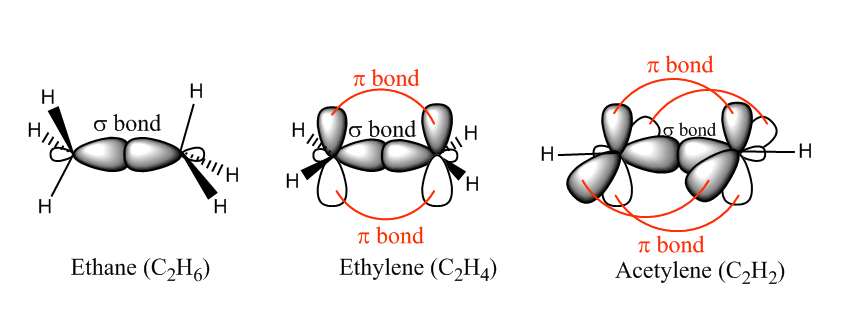
The following figure shows the bonding between two carbon atoms in ethane (C₂H₆), ethylene (C₂H₄) and acetylene (C₂H₂), for which possess a single bond, double bond, and triple bond, respectively. When a single bond is formed, we refer it to as σ bond. When multiple bond is formed, we have π bond. The π bond is formed by interaction between the two neighboring unhybridized 2p_z orbitals. Each 2p_z orbital has two lobes with different phase, and for a bonding orbital the two phases match.

Example: Identify hybridization of all carbon atoms in the following molecule.

+ Hybridization and geometry relation.

We can go futher, and assign oxygen at the top and nitrogen with single bonds are sp³ and the double bonded oxygen is sp² hybrid.

Molecular Orbital Theory

At the beginning of this chapter, we talked about the model of hydrogen moleucle using the Coulomb interactions. Then, from two hydrogen atoms approach each other to have overlapping tails of the two 1s orbitals, which gave rise to a set of molecular orbitals.

Again, for simplicity, we illustrate the formation of molecular orbitals using H₂. Each hydrogen atom has one electron in 1s orbital. When the chemical bond forms, the interaction of two waves (1s wave functions) give rise to two molecular orbitals. The bonding orbital, labeled σ is more stable than the original two 1s orbitals. The other molecular orbital is labeled as σ*, which is also known as anti-bonding orbital.

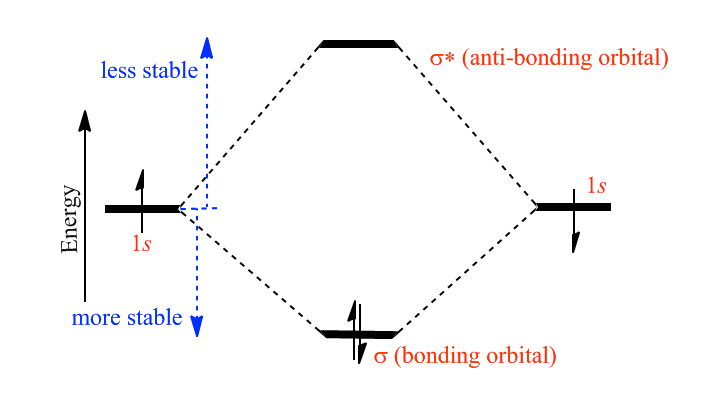
Since the anti-bonding orbital, in the picture below, is higer than the respective atoms, therefore, it is not stable. It means that if electrons are placed in the anti-bonding orbital, the molecule can dissociate. The stability of molecule can be calculated by occupation of orbitals to calculate bond order, O_B by using the following equation. $O_{B} = \frac{n_{b e} - n_{a e}}{2}$ Here n_be is the number of bonding electrons and n_ae is the number of antibonding electrons. If we use this equation for H₂^-, the bonder order is 1/2, and for He₂, O_B = 0, and these tell you that H₂^- molecule is weakly bound and for He₂ is expected of no existence.

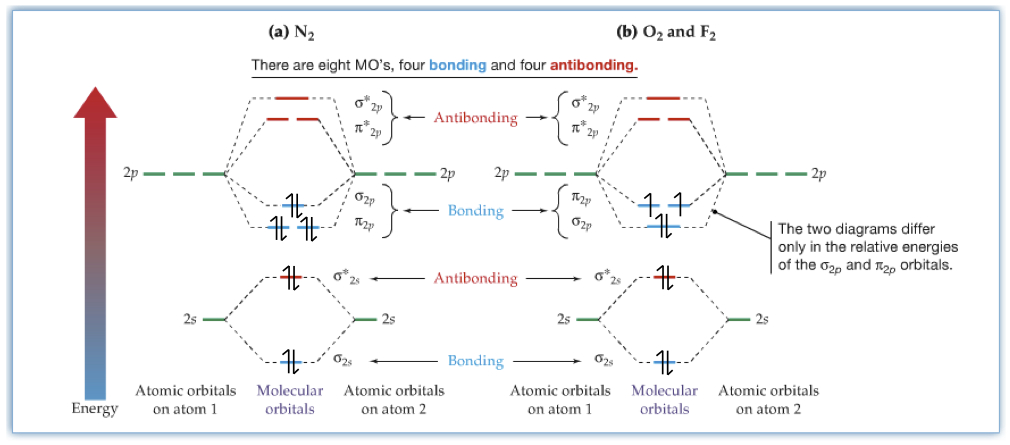
Molecular orbitals of more complicated molecules are very difficult to obtain from a pen and paper. Today with modern computers, we crunch out the molecular orbital calculations. One of the early triumphs of the molecular orbital theory is the diradical character of O₂ molecule. When liquid O₂ is placed between two magnets, surprisingly the liquid sticks to the magnet. It only means that O₂ is magnetic. From Lewis structure, we see that there should be a double bond between the two oxygen atoms, hence there is no magnetic character, called diamagnetic. However, the detailed molecular orbital calculations show that oxygen is paramagnetic, which means that the molecule possesses magnetic character. The following picture compares that the moleuclar orbitals of N₂, and O₂. The difference between the molecular orbitals is where the bonding orbitals labeled as π_2p and σ_2p . The order is reversed in O₂, which makes the occupation of π_2p to be one electron each and they are unpaired.

Chapters 7-10. The Electronic Structure of Atoms to Chemical Bonding

Combined chapters for understanding the electronic structure

Mathematical relationship of wave length with misterious whole number!

Lattice Energy