Valence Shell Electron Pair Repulsion Theory
3-D structures of Molecules We now now how to draw a structure of a molecule in 2-D by using connecting unpaired electrons.
Molecules in reality is not two-dimensional. They are actually three-dimensional entity, and have trend to assume certain shapes. In this section we use Valence Shell Electron Pair Repulsion (VSEPR) theory to deduce 3-D structure of molecules. 3-D structure is extremely important, since in many instances, reactivity of molecules can be determined.
From the Coulomb's law, the first equation at the very top of this page, the charges of the same sign have repulsive interaction. Considering the fact that molecules are made of chemical bonds and some have lone pair electrons, there must be bond-bond repulsive interaction or bond-lone pair interaction. The VSEPR theory utilize these repulsive interactions to deduce the 3-D structures of molecules. They key is to minimize the repulsive interactions in a molecule.
VSEPR Theory We must count and classify the number of charge clouds in order to deduce three-dimensional structure.
- # of Bonds: Regardless of having a multiple bond, chemical
bond(s) between two nuclei is considered as one charge cloud.
- # of Lone Pairs: Count the number of lone pair electrons.
- Total # of Charge Cloud: Add the # of bonds and # of
lone pairs.
By using the following table, one can deduce the 3-D structure.
| Charge Clouds | # of Bonds | # of Lone Pairs | Structure | Example | |
|---|---|---|---|---|---|
| 2 | 2 | 0 | Linear | CO2 | 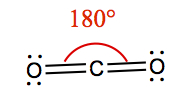 |
| 3 | 3 | 0 | Trigonal Planar | COH2 | 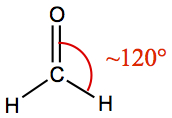
|
| 2 | 1 | Bent | SO2 | 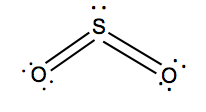 | |
| 4 | 4 | 0 | Tetrahedron | CH4 | 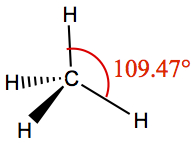
|
| 3 | 1 | Trigonal Pyramid | NH3 | 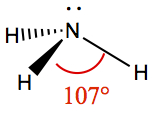 | |
| 2 | 2 | Bent | H2O | 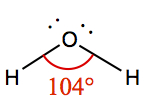 | |
| 5 | 5 | 0 | Trigonal Bipyramidal | PF5 | 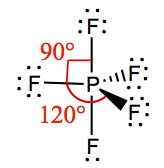
|
| 4 | 1 | See-Saw | SF4 | 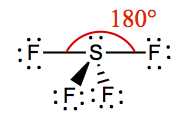 | |
| 3 | 2 | T-shaped | ClF3 | 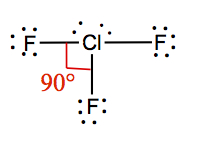 | |
| 2 | 3 | Linear | XeF2 | 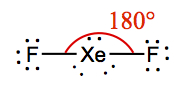 | |
| 6 | 6 | 0 | Octahedral | SF6 | 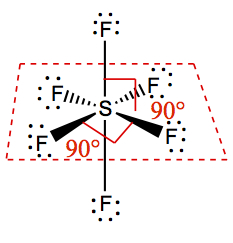
|
| 5 | 1 | Square Pyramidal | ClF5 | 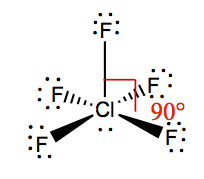 | |
| 2 | 2 | Square Planar | XeF4 | 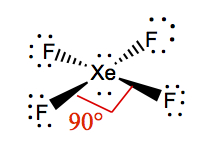 | |
In order for you to determine the 3-D structure, you must first be able to draw a Lewis structure of the molecule so that the number of charge clouds, the number of bonds, and the number of lone pairs are known.
Valence Bond Theory and Hybrid Orbitals
When drawing a Lewis structure, we used a pair of valence electrons from each nucleus in the molecule to form a chemical bond.We also talked about formation of chemical bond in H2 from two hydrogen atoms; two 1s orbitals approach each other with overlapping tails, which gave rise to bonding and antibonding orbitals.
sp3 Hybrid Orbitals: Upon forming a chemical bond, for example in CH4 1s orbitals of four hydrogens overlap with the carbon's 2s and 2p orbitals, because carbon's valency is 4. Since methane assumes tetrahedral structure, each of the four bonds has to be completely equivalent. This means that carbon's atomic orbitals have to be modify to accomodate the four hydrogens' 1s orbitals. The accomodation comes via forming a so-called, hybrid orbitals. Carbon needs to use four of orbitals (2s, 2px, 2py, and 2pz) and the four orbitals mixes to obtain four equivalent atomic orbitals, known as sp3 hybrid orbitals, as shown below. The sp3 orbital overlaps with hydrogen's 1s orbital to form a covalent bond, called σ bond.
The angle between each lobe assumes 109.47° since the sp3 carbon is tetrahedral.
sp2 Hybrid Orbitals: If a carbon atom is in a double-bond environment, such as C2H4 (ethylene), the carbon is hybridized to become sp2 hybrid orbital. As we have seen in the VSEPR theory, double-bonded carbon has a trigonal planar structure with approximate bond angle of 120°. In order to have three σ bond connections, one 2s and two 2p orbitals have to be mixed. This leaves unhybridized 2p orbital. The unhybridized 2p (typically 2pz orbital) orbital is involved as the second bond to another carbon. We call this a π bond . The bond angle between the lobes of hybridized orbitals are about 120°, and each lobe is coplanar. The unhybridized p orbital is 90° to the plane. The sp2 hybrid orbital is shown below.
sp Hybrid Orbitals: In this case, a carbon atom is in the triply bonded enviroment. The VSEPR theory predicts that acetylene (C2H2) is a linear molecule. Each carbon is bonded to two other atoms, hence only two atomic orbitals, namely one 2s and one 2p orbital are needed for hybridization. Two other 2p orbitals are unhybridized. These unhybridized p orbitals are involved in two π bonds.
The following figure shows the bonding between two carbon atoms in ethane (C2H6), ethylene (C2H4) and acetylene (C2H2), for which possess a single bond, double bond, and triple bond, respectively. When a single bond is formed, we refer it to as σ bond. When multiple bond is formed, we have π bond. The π bond is formed by interaction between the two neighboring unhybridized 2pz orbitals. Each 2pz orbital has two lobes with different phase, and for a bonding orbital the two phases match.
Molecular Orbital Theory
At the beginning of this chapter, we talked about the model of hydrogen moleucle using the Coulomb interactions. Then, from two hydrogen atoms approach each other to have overlapping tails of the two 1s orbitals, which gave rise to a set of molecular orbitals.
Again, for simplicity, we illustrate the formation of molecular orbitals using H2. Each hydrogen atom has one electron in 1s orbital. When the chemical bond forms, the interaction of two waves (1s wave functions) give rise to two molecular orbitals. The bonding orbital, labeled σ is more stable than the original two 1s orbitals. The other molecular orbital is labeled as σ*, which is also known as anti-bonding orbital.
Since the anti-bonding orbital, in the picture below, is higer than the respective atoms, therefore, it is not stable. It means that if electrons are placed in the anti-bonding orbital, the molecule can dissociate. The stability of molecule can be calculated by occupation of orbitals to calculate bond order, OB by using the following equation. Here nbe is the number of bonding electrons and nae is the number of antibonding electrons. If we use this equation for H2-, the bonder order is 1/2, and for He2, OB = 0, and these tell you that H2- molecule is weakly bound and for He2 is expected of no existence.
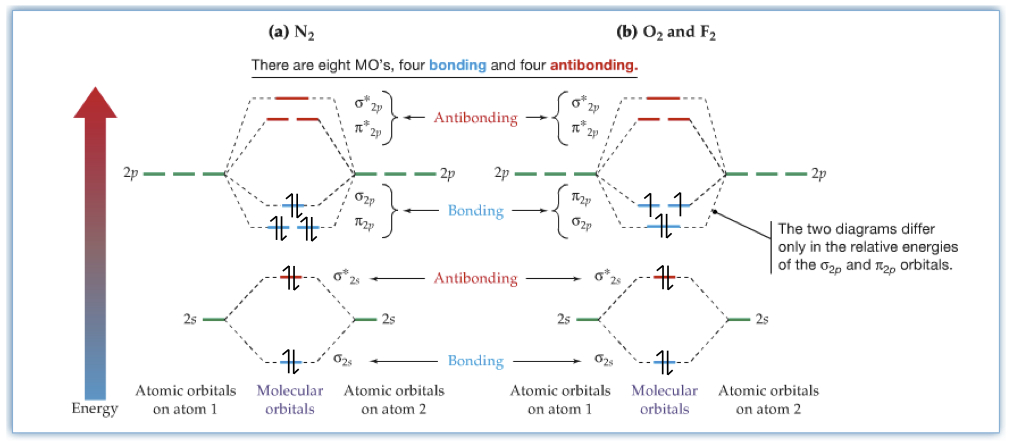
Molecular orbitals of more complicated molecules are very difficult to obtain from a pen and paper. Today with modern computers, we crunch out the molecular orbital calculations. One of the early triumphs of the molecular orbital theory is the diradical character of O2 molecule. When liquid O2 is placed between two magnets, surprisingly the liquid sticks to the magnet. It only means that O2 is magnetic. From Lewis structure, we see that there should be a double bond between the two oxygen atoms, hence there is no magnetic character, called diamagnetic. However, the detailed molecular orbital calculations show that oxygen is paramagnetic, which means that the molecule possesses magnetic character. The following picture compares that the moleuclar orbitals of N2, and O2. The difference between the molecular orbitals is where the bonding orbitals labeled as π2p and σ2p . The order is reversed in O2, which makes the occupation of π2p to be one electron each and they are unpaired.
Bond Polarity
Remember that Fluorine is has the highest value of electronegativity, χ? Due to electronegativity difference, Δχ, b/w two atoms, bond would polarize.
If the Δχ = 0, then the bond is said to be non-polar.
If the Δχ is non-zero, the bond is polar.
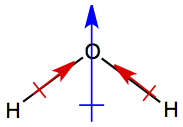
So for molecule N=O, we have
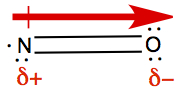 As it is seen, arrow indicates the dipole moment of the bonds between
N and O, and the arrow points toward more negative side, indicated with
δ-, and the other end is more positive side,
δ+. This is so because oxygen is closer to
F in the periodic table than nitrogen.
As it is seen, arrow indicates the dipole moment of the bonds between
N and O, and the arrow points toward more negative side, indicated with
δ-, and the other end is more positive side,
δ+. This is so because oxygen is closer to
F in the periodic table than nitrogen.
 Adding all Polarities of bonds →
molecular dipole moment, μ
Adding all Polarities of bonds →
molecular dipole moment, μ
The bond dipole moments of O-H bonds (red arrow) in water points toward oxygen atom. When these two bond dipoles are added together, molecular dipole moment (blue arrow) is produced. As in the bond dipole, the direction the arrow is pointing has partially negative charge, and the opposite end has partially positive charge.
In order to deduce dipole moments of molecule is to know the 3-D structure of the molecule. Then, draw in the bond dipoles (red arrows). We consider C-H and C-C bonds to be non-polar bonds, therefore we don't draw in the arrow for these bonds. After bond dipoles are drawn in, all bond dipole vectors are added, and the resulting vector is the molecular dipole moment (blue arrow ).
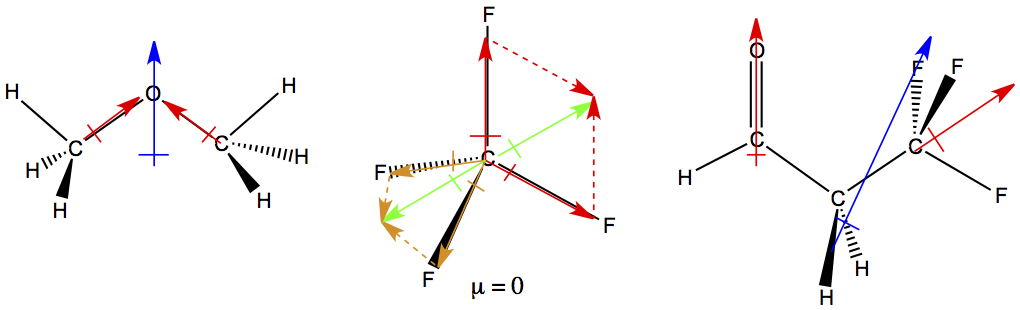
For CF4, two of the red bond dipoles form a resultant green dipole in the plane of the computer monitor. For other two bond dipoles, with orange color, form another green resultant pointing in the opposite direction. And, they cancel each other, therefore the moleuclar dipole moment of CF4 is zero.
Intermolecular Forces
Forces b/w molecules
Forces responsible for condensing gas into liquid and liquid into solid
Forces responsible for making different compounds to have different melting point and boiling point.
Four types:
 Force exits between ion and molecule with permanent dipole moment. Cation is attracted to the partially negative side of the polar molecule, and anion is attracted to the partially positive end of the polar molecule.
Force exits between ion and molecule with permanent dipole moment. Cation is attracted to the partially negative side of the polar molecule, and anion is attracted to the partially positive end of the polar molecule.
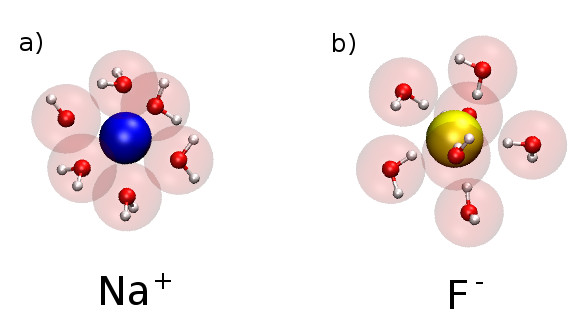 Water surrounds Na+ ion in a) and F- ion surrounded by water in b). The red sphere in water is the oxygen atom. Notice that the oxygen is pointing toward Na ion, and the hydrogen atoms point toward F ion.
Water surrounds Na+ ion in a) and F- ion surrounded by water in b). The red sphere in water is the oxygen atom. Notice that the oxygen is pointing toward Na ion, and the hydrogen atoms point toward F ion.
 Interaction b/w two molecules with permanent dipole moments. The partially positive charge side is attracted toward partially negative side, and vise versa.
Interaction b/w two molecules with permanent dipole moments. The partially positive charge side is attracted toward partially negative side, and vise versa.
So, if you have a bunch of N=O molecules, you'd see the packing of molecules as shown on the left diagram in the figure below. On the right diagram negative-negative interactions and positive-positive interactions, both represented by green arrows, are the repulsive interaction. So the structure is unstable. It'd eventually become the same packing as on the left.
Dipolar vs non-dipolar interactions
| N2 | NO | O2 | |
| Dipole(debye) | 0 | 0.153 | 0 |
| Mass (g/mol) | 28 | 30 | 32 |
| Boiling pt(K) | 77 | 121 | 90 |
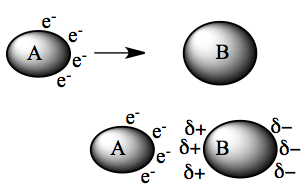
As they are close to each other, B sees the electrons on A, and the electrons on the left-side of B starts to avoid the approaching A (lower diagram on left). This induces polarity on molecule B, which in turn can polarize A as well. This is the source for the attractive force between non-polar non-ionic molecules.
If the molecule is easy to deform → said to be Polarizable.
| Halogen | mp (K) | bp (K) |
|---|---|---|
| F2 | 53.5 | 85.0 |
| Cl2 | 171.6 | 239.1 |
| Br2 | 265.9 | 331.9 |
| I2 | 386.8 | 457.5 |
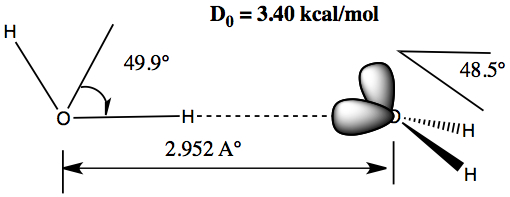
Sharing of hydrogen between two molecules
Each molecule must act as both the donor and acceptor.
The picture on the right is a dimer of water. The molecule on left is the H-donor and the one on right is the acceptor.
The shared hydrogen is co-linear with the lone pair-H-donor.
The binding energy for water dimer is quite small (3.4 kcal/mol). But, this is the force holding two strands of DNA.
Comparison of the strength of intermolecular forces
| Ion-Dipole | 10 - 50 kJ/mol | 2 - 12 kcal/mol |
| Dipole-Dipole | 3 - 4 kJ/mol | 0.5 - 1 kcal/mol |
| Dispersion | 1 - 10 kJ/mol | 0.2 - 2 kcal/mol |
| H-bond | 10 - 40 kJ/mol | 2 - 10 kcal/mol |