Energy and Its Conservation, First Law of Thermodynamics
Energy—ability to do work or to supply heat. Mathematically,
where q = heat and w = work.
Heat—Thermal energy transferred from one object to another.
Another way of defining energy is by
where T = kinetic energy and V is the potential energy. The kinetic energy is the energy of motion for a particle with mass m, and has where v = velocity of particle. The potential energy is related to position of that particle. The functional form of potential energy differs in different systems. For example, we have seen in Chapter 7 that interaction energies between particles in H2 molecule is given by Coulomb interaction. The distances, hence position, between two charges give the strength of the interaction.
Energy conservation: The figure below explains the relationship between energy (total energy), kinetic energy, and potential energy. Let's say that you place a ball in a symmetrical bowl-like environment without friction. The ball has a mass, m. Since we are dealing with rolling a ball, we are dealing with the potential energy in gravity which has dependence on mass and the height of the ball. The potential energy is then given by
where g is the gravitational force on earth, 9.81 m/s2, and h is the height of the ball compared at the bottom of the well (h = 0). Energy unit is in Joules, J = 1 kg m2/s2. When you let the ball go, the position of where you put the ball, labeled with h0 = 1, the kinetic energy is zero at the instance of letting the ball go. The ball starts to accerelate until it passes the bottom of the well, labeled h1 = 0, at which the potential energy is zero, but kinetic energy is maximum, because of the pull of the gravity. The ball then starts to slow down until it reaches at the same height as h0 on the opposite side, labeled h2.
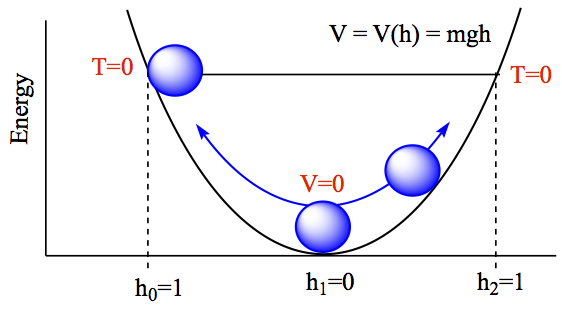
At each point of passage, the total energy is exactly the same.
- at h0, T = 0, E = V(h0),
- at h1, V = 0, E = T(h1),
- at h0, T = 0, E = V(h2),
- at any other position h, T ≠ 0, V ≠ 0, E = T + V
So, from these and in general, total energy of a process is conserved. Or total energy of the system is unchanged in a closed system.
Internal Energy and State Function
Thermodynamic system: An isolated system, i.e. the system of interest such as moleucules being surrounded by surrounding, and the surrounding is enclosed by an insulated wall so that no heat, no work, no molecules escape from the surrounding. The system can exchange heat and/or work to the surrounding.
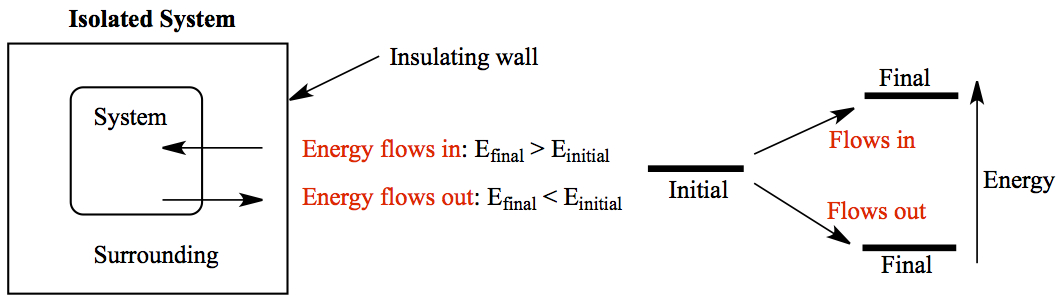
The energy of the system, internal energy which consists of molecular motions and interaction between them, can change so that the final energy can be higher or lower than its initial energy. When the final energy is higher than the initial, then the energy flows into the system from the surrounding. On the other hand, if the final energy is lower, the energy flows out of the system to the surrounding. These are depicted above.
State Function—if the quantity is independent of path, we call it state function. Energy is a state function. So, when calculating the overall energy change in the system, all you need to do, is to calculate the difference between the final energy and initial energy,
Expansion Work
Work: In general work is force times distance. In this chapter, we only consider work involving expansion work. Under ordinary laboratory conditions, atmospheric pressure, p, is constant. So, when expansion work is performed by the system, work done by the system is given by the following equation,
where ΔV is the change in volume, and p is the pressure. Pressure is measured in atmosphere, atm, and the volume is measured in L with if pΔV = 1 atm L = 101 J.
Since ΔV is defined as Vfinal - Vinitial, if the gas is expanded, meaning that Vfinal > Vinitial, the sign of the work is negative. In this case, it is said that the work is done by the system. If, however, the gas is compressed, then w is positive.
Energy and Enthalpy
We already saw that ΔE = q - pΔV. Since we can measure heat, by observing the temperatrue change, we can rearrange the equation and solve for q. Then, we get,
If there is no work, that is no change in volume, q = ΔE.
If the pressure is constant, then q = ΔE + pΔV. We define this heat measured at constant pressure to be enthalpy change, ΔH.
Enthalpy is state function, like energy. So, enthalpy change is not depended on the path. When the enthalpy of final state is higher than the initial state, it is said to be endothermic and one must inject heat into the system to achieve the final state. On the other hand, if the final state is lower in enthalpy, it is said to be exothermic where heat is generated (or liberated) by the system.
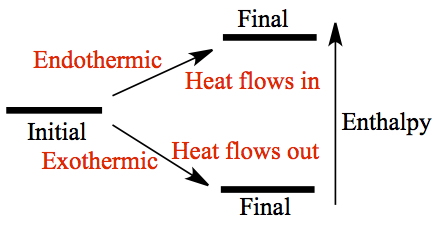
Thermodynamic Standard State
It is convenient for us to use standardized thermodynamic quantity, so that when reporting values can be compared directly.Thermodynamic standard state—most stabel form of a substance at 1 atm pressure and at specified temperature, usually 25°C. If solution is involved, the concentration is 1 M.
We denote enthalpy change measure at the standard state to be ΔH° ← notice a knot!
Enthalpy of Physical and Chemical Change
Enthalpy change associated with physical change Melting process (fusion), and boiling (vaporization) needs extra heat to melt or vaporize. For H2),
and
Then, by the virtue of enthalpy being state function, sublimation process is
Enthalpy change associated with chemical change Of course, we are now talking about heat generated or absorbed by the reaction. We call the heat, heat of reaction. We write down the heat of reaction at the end of chemical equation, for example, combustion of propane (C3H8)
The chemical equation that includes thermodynamic data, such as heat of reaction, is called thermochemical equation. In the above example, we have standard heat of reaction, and the reaction is exothermic.
If you reverse the reaction, that is,
the reaction becomes endothermic.
If on the other hand, the reaction is doubled the above,
If halved, the value of the ΔH° must be multiplied by ½.
Calorimetry and Heat Capacity
Heat Capacity Since heat, q, has to do with temperature change, heat and temperature change must be proportional to each other, i.e.
where ΔT = Tfinal - Tinitial. If you want an equation, instead of proportionality, we can put a proportionality constant, C, such that,
and C is called heat capacity. Heat capacity tells how much energy required by a substance to raise its temperature by 1°C. It has a unit of J/°C.
We can make heat capacity dependent on mass, it means that,
where m is the mass, and csp is specific heat. Specific heat is defined as energy required by 1 g of substance to raise its temperature by 1°C. Its unit is J/(°C g).
Furthermore, we can make depended on number of moles, as well. In such a case,
where n is the number of moles, and cm is the molar heat capacity, which is defined as energy required to by 1 mol of substance to raise its temperature by 1°C. Its unit is J/(°C mol).
Using these, we can measure heat.
Calorimeter—a device to measure heat. Some devices are rather elaborate, but the priciples are the same for any calorimeter. So, we illustrate a calorimetry experiment using a styrofoam coffee cup, as follows.
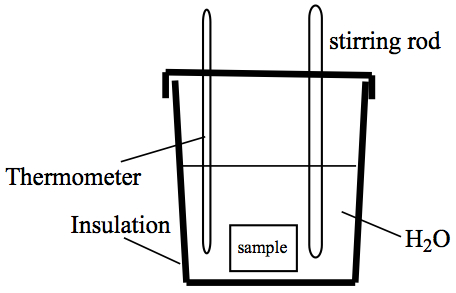
The styrofoam cup acts as insulating walls in the description of isolated system at the beginning of the chapter. We need to obtain temperature readings, so a thermometer is necessary, and in order to keep the temperature of water to be consistent throughout the cup, a stirring rod is provided. A calorimeter usually use water as the surrounding to the sample chamber. For simple experiments, such as the ones we perform in our labs, it doesn't have to have the sample chamber.
Specific heat of water is given as 4.182 J/(°C g).
In elaborate experiments, we can not use specific heat of water as the specific heat of surrounding, since the wall might absorb some of the heat and it might change the value. The specific heat of the calorimeter must be independently determined. For us in this course, we use the specific heat of water as the specific heat of calorimeter.
If the system releases heat to the surrounding, the surrounding receives the same amount of heat. So the amount of heat transferred is exactly the same magnitude. However, in this case, system is "pushing" the heat, and the surrounding is "pulling" the heat. This can be considered as opposite effect. In terms of mathematics, we denote this "push-pull" system to be,
where qsys is the heat from/to the system, and qcal is the heat to/from the calorimeter (surrounding).
If we use the specific heat equation for q, then one can expand the equation above as,
The ΔTsys on the left-hand side of the equation, is given by Tfinal - Tinitial of the system, while ΔTsys on the right-hand side of the equation, is given by Tfinal - Tinitial of the calorimeter or the surrounding. In either case, Tfinal is common to both the system and the surrounding.
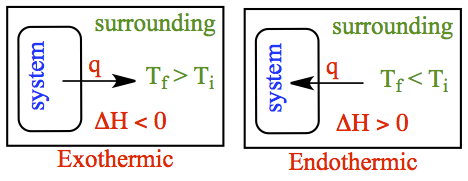
If the system is exothermic, then the heat is pushed into the surrounding. Hence the temperature of the surrounding becomes higher, compared to the initial temperature. On the other hand, if the system is endothermic, the heat is extracted from the surrounding and provided to the system. It means that the final temperature of the surrounding must become lower than the initial temperature. These situations are shown in the figure to the right.
ΔT is common to both water and metal, when it reaches equilibrium. We can use the "push-pull" heat equation,
Expand this equation,
The balanced equation is,
The rest is dimensional analysis, using 4.88g of barium hydroxide hexahyrate.
Hess's Law
When multiple stpes are involved in the reaction, the sum of all enthalpy changes in different stpes give the overall enthalpy of reaction.For example, we will look at the heat of reaction of the following.
Instead, we can do two separate experiments that are amenable to our course. We carry out the heat measurements of the following two reactions. The experiment and how to obtain ΔHrxn is illustrated in the example below. Before we move to the example, few tips when combining chemical equations.
When adding two equations We want the following equation.
The two steps involved in this reaction, and they are:
D → 2C ΔH2
In addition, there is no C in the overall equation, therefore, we must have the same number of C in both reactions. It means that we need to multiply 2 to the first reaction, and 3 to the second. Then, we have,
6C → 3D -3ΔH2
Here is an example of experiment we actually do in our lab.
Rxn 2 MgO(s) + 2HCl(aq) → MgCl2(aq) + H2O(l) ΔH2 = ?
In addition to above two reactions, we need the heat of formation of water to be able to make the overall equation to be correct.
Say that the following is the result of two reactions:
| mass | Volume | Tinitial | Tfinal | |
|---|---|---|---|---|
| Rxn 1 | 0.202g (Mg) | 100 mL HCl | 21.7°C | 31.7°C |
| Rxn 2 | 1.040g (MgO) | 100 mL HCl | 22.1°C | 30.2°C |
| The concentration of HCl used in both cases is 2.87 M, and its specific heat is 3.47 J/g°C. The density of HCl(aq) at the concentration is 1.048 g/mL. | ||||
Heat of reaction is calculated by by using,
Similar calculation for rxn 2 yields qcal = 2945.61 J. Therefore, qrxn 1 = - qcal = -3636.56 J, and qrxn 2 = - 2945.61 J.
Now we need to know the number of moles of Mg or MgO in the respective solution, and they are,
Dividing the qrxn 1 by the number of moles of Mg, qrxn 1 = -437.6 kJ/mol(Mg). Similarly, qrxn 2 = -114.7 kJ/mol(MgO).
Now we have to rearrange Rxn 1, Rxn 2, as well as the heat of formation of H2O to obtain the equation of interest.
Rxn 1 stays the same, but rxn 2 needs to be reversed, meaning that multiply the rxn 2 equation by -1. Furthermore, we need to cancel H2 in rxn 1, therefore, we need to divide the heats of formation of water by 2.
Rxn 2
MgCl2(aq) + H2O(l)
→
MgO(s) + 2HCl(aq)
ΔH2 = +114.7 kJ/mol
ΔHf
H2(g) + ½O2(g)
→
H2O(l)
ΔHf = -285.8 kJ/mol
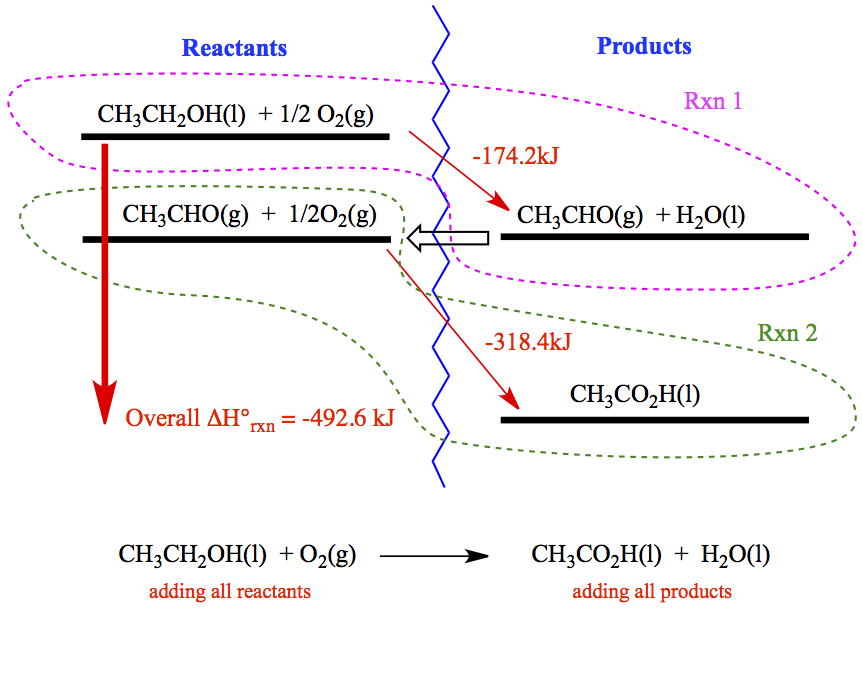
Hess's law can be illustrated in terms of energy diagram. For a reaction,
Rxn 2 CH3CHO(g) + ½O2(g) → CH3CO2H(l) ΔH° = -318.4 kJ
Standard Heats of Formation
Formation Reaction—reaction to make a compound from its stable elements. The reactants are the elements and the product is the moleucle of interest. For example, the formation reaction for water is,
as making liquid water from its elements, hydrogen molecule and oxygen molecule. The enthalpy associated with the formation reaction is called, heat of formation, ΔHf . As we have seen already,
If we measure the heat of formation at standard state, then the heat of formation is standard heat of formtion, ΔH°f.
Heats of Formation of Elements are zero! So, H2, O2, C(graphite), Cu, Fe, Cl2 have all zero for its formation enthalpy.
Standard Reaction Enthalpy. What's useful about the heats of formation, is the fact that one can obtain heat of reaction, by the following for the reaction,
where small letters, a, b, c, and d are the stoichiometry of the balanced chemical equation. Then,
This is quite useful because you don't have to know anything about the reaction to know the enthalpy of the reaction, simply by looking up on a table of ΔH°f (In our case, look at Appendix B in our text).
Bond Dissociation Energies
We have looked at the energy profile of a diatomic molecule, the last picture of this section. We discussed that when making a chemical bond from two atoms, energy is released. When a chemical bond is to break, one must input energy into the molecule. The energy required to break a bond into two fragments of molecule is called bond energy.
The bond energies can be useful in estimating the reaction enthalpy. Afterall, we are only rearranging chemical bonds during chemical reaction. So, for example, two ethane (C2H6) react to make butane, C4H10, and H2, as shown below.

Using this table, we have,
| Type | #affected bonds | Energy | Total |
|---|---|---|---|
| | |||
| Reactants | |||
| C—H | 2 | 410 x 2 | 820 |
| total of reactants | 820 | ||
| | |||
| Product | |||
| C—C | 1 | 350 x 1 | -350 |
| H—H | 1 | 436 x 1 | -436 |
| total of product | -786 | ||
| | |||
| ΔHestimated =
34 kJ/mol(8 kcal/mol) Actual = 42 kJ/mol(10 kcal/mol) |
|||
In this example, the estimated enthalpy of reaction is 34 kJ/mol, while calculating it from the heats of formation yields 42 kJ/mol. The difference between the estimated by the average bond dissociation energy and by heats of formation is quite small. We can do the similar series of hydrocarbons by breaking two C—H bonds and forming one C—C bond and one H—H bond. With our estimation, all should come out to be 34 kJ/mol, is this value correct for different reactions? Here is the answer,
Propane (C3H8) + Propane (C3H8) → Hexane (C6H14) + H2 ΔH° = 43 kJ/mol
Propane (C3H8) + Butane (C4H10) → Heptane (C7H14) + H2 ΔH° = 43 kJ/mol
Butane (C4H10) + Butane (C4H10) → Heptane (C8H18) + H2 ΔH° = 43 kJ/mol
So, as long as the reaction of this type or similar, one can estimate the reaction enthalpy by using the average bond energies.
If the reaction is more ivolved, this estimate just doesn't work. For example, in the following example the estimation breaks down.
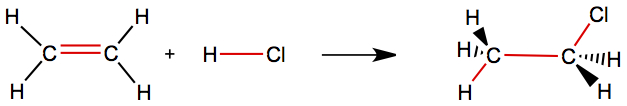
In this case we break two C—Hbonds and one H—Cl bond, and form one C—H bond and one C—Cl bond. In this case the estimation fails.
Using the average bond energy, we obtain ΔHestimate = +70 kJ/mol, while calculating it from the heats of formation, it is -69 kJ/mol. Therefore, it is off by nearly 140 kJ/mol and has wrong sign for the reaction enthalpy! In this case, the reaction is not just simply breaking bonds and forming the similar bonds; we have change in hybridization of both carbons from sp2 to sp3.
Entropy
Spontaneity. Our experience tells us that heat never seems to flow from cold to hot object in a natural way; it is always one direction, from hot to cold. Heat can not be coveyed from a cold object to hot object spontaneously. For example, if you have two pieces of metal with one piece heated to high temperature (metal 1 in the figure), and the second piece originally at room temperature (metal 2). It means that temperature of metal 1 is higher than that of metal 2. In this case, direction of the heat flow is to the right. This natural tendency for heat to flow in one direction is the statement of 2nd law of thermodynamics .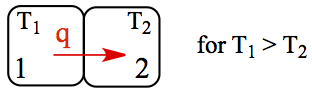
Some chemical reactions are spontaneous. For example, ice melts at room temperature, despite it must overcome the heat of fusion, ΔHfus > 0. Or when you turn your iPod on, electricity flows through the system immediately. This is due to that fact that red-ox reaction takes place in the battery to supply the electrons needed by the device.

Also from our experience that for a gas in a balloon the situation on right is much more likely than the spontaneous organization of gas molecules into a corner of the balloon at the same temperature! (Of course, if you lower the temperature, the gas molecules would condense into a liquid.
As far as energy is concerned, we have talked about energy has tendencey to flow toward lower energy side, since lower energy means the state is more stable. ....
Free Energy
Spontaneous process occurs when the Gibbs free energy is lower in the product, compared to the reactant. Gibbs free energy combines the enthalpy and entropy contributions in the spontaneous processes. For a chemical reaction, the Gibbs free energy change is given as,
Just as enthalpy and entropy are state functions, Gibbs free energy is also a state function. As shown in the figure below, spontaneity only comes when the ΔG < 0.
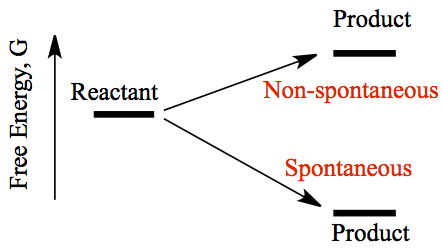
If the ΔG > 0, the reaction is non-spontaneous. If the Δ G = 0, the reaction is said to be in equilibrium where the rates of forward reaction is the same as that of the reverse direction. In such a reaction we use a double-arrow sign, ⇄ in chemical equation to indicate there is an equilibrium. Do you remember how we represent weak acids? For acetic acid, we wrote,
In order to determine the spontaneity of chemical process, there are three factors: 1) ΔH, 2) &DeltaS, and 3) T. Following table summarizes.
| Signs of | |||
|---|---|---|---|
| ΔH | ΔS | T | Spontaneity |
| + | - | high | spontaneous |
| + | - | low | non-spontaneous |
| + | + | high | non-spontaneous |
| + | + | low | non-spontaneous |
| - | - | high | non-spontaneous |
| - | - | low | spontaneous |
| - | + | high | spontaneous |
| - | + | low | spontaneous |
Since ΔG = ΔH - TΔS, and at equilibrium ΔG° = 0. It means that this is the temperature at which the reaction becomes spontaneous or nonspontaneous. Then, that temperature is
Above this temperature, the entropy term is large positive number, which becomes larger than the negative enthalpy term. Therefore, the overall free energy becomes positive, hence non-spontaneous.