 |
Department of Chemistry Chem 3 (Introduction to Chemistry) Dr. Nikita Matsunaga |
 |
Department of Chemistry Chem 3 (Introduction to Chemistry) Dr. Nikita Matsunaga |
Dimensional analysis is a very powerful method of calculating quantities one needs as a chemist. One can calculate, for example, an amount of substance needed to make a certain concentration of aqueous solution. The main idea of the method is to cancel out the units appearing in both the numerator and the denominator. Therefore, the units of the particular numerator-denominator pair has to be exactly the same. At the end, the unit that you are looking for on the left-hand side of the equation, is matched by the unit that is left over by canceling all other units on the right-hand side. The details of the method are shown below.
Step-by-step Dimensional Analysis:
The analysis is illustrated by the following example:
How many grams of NaCl is needed to make 150 mL solution of 2.00 M NaCl, given that the molar mass of NaCl is 58.4 g/mol?
The first thing one has to know,
obviously, is what units you are trying to get at the end. Hence, this
becomes your question. Put unit next to the question mark on the
left-hand side of the equation. At the end of a calculation, the unit is
compared with the uncanceled unit on the right-hand side of the equation.
In our example, we start our problem by writing:
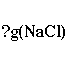
It is important to write down not
only the unit itself, but substance to which the unit belongs. So, we
write g(NaCl), and not just g. You will see in later
examples why it is important to include the substance.
We have to equate the grams of
NaCl on the left-hand side of the equation to something that is appropriate
for us to start our calculation. What is appropriate to put on the right-hand
side of the equation? Generally, in this kind of problem, there are many
givens available for you. One group is conversion factors that are made
of compounded units, such as g/mol, g/mL, or mol/L. Another group has
one unit alone, and this is the one you want to start your calculation with.
In our case, the only simple unit that is given is the volume of NaCl
solution needed. Hence,
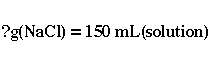
As it was mentioned in the
introduction, the name of the game here is to cancel out the unit that
you start with. This unit should appear in the denominator of the
conversion factor. In our example, we would like to cancel the unit,
mL(solution), by extending our equation with a conversion factor
in parentheses. There are two givens with compounded units. They are
58.4 g/mol (or 58.4 g(NaCl)/mol(NaCl)) and 2.00 mol(NaCl)/1.00 L(solution)
(or 2.00 mol(NaCl)/1000 mL(solution)) as a definition of 2.00 M NaCl. In
order to cancel the mL(solution), we shall use the definition of 2.00 M
NaCl solution. Therefore, we get
Check to see if the unit that was
given, mL(solution), matches with the denominator of the 2.00 M definition.
Again, place the cursor over the equation above.
When the product of the numerators
is divided by the product of the denominators, you get an answer, 17.533
g(NaCl). The significant figure in this problem is three, therefore you
should report your answer as 17.5 g(NaCl). So, you will need 17.5 g(NaCl)
to make 150 mL solution of 2.00 M NaCl solution. Pretty cool, eh!
Additionally, there is no reason for
us to keep 58.4 g(NaCl) in the numerator in all calculations. It can be
placed in the denominator as well, in which case your numerator is 1
mol(NaCl). The 58.4 g/mol really means 58.4 g(NaCl) = 1
mol(NaCl)!
Here is the final answer.
Want to practice further?
For now, I only have two parentheses, but I'm trying to extend the program
to add more parentheses automatically as problems get larger. I listed
below some more excercise questions that apply for this calculator.
Dimensional Analysis Calculator
Additional Questions:
last updated 12/06/98
We use the other conversion factor, 58.4 g/mol, to finish off this problem.
By placing 58.4 g(NaCl) in the numerator and 1 mol(NaCl) in the
denominator, we accomplished our mission.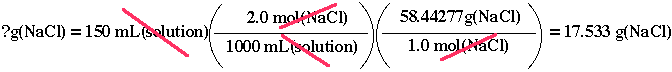
A dimensional analysis calculator is
shown below. You can apply the same techniques discussed above to use this
calculator. Let me explain what you can type in. As you can see, each
field is separated into two components, a value denoted as x1 and its unit
denoted as u1 for the first set of data. You can type the units and the
values we used above into this calculator. It will check to see if you
have the right units at the right places, then it calculates the answer
for you with the right unit.
Back to
Dr. Matsunaga's homepage