Chapter 3 Mass Relationships in Chemical Rxns

Atomic Mass

Atomic mass is represented by atomic mass unit (amu), and is defined by $1 a m u = \frac{m (C - 12)}{12} = 1.660539 \times 10^{- 24} g$

where m(C-12) is the mass of carbon-12 isotope.

If you look at Xe atom in the Periodic Table, forexample, the average mass of Xe is 131.29 amu.

Example: How many atoms are there in 10.0 g of Na?

As we've seen in Chapter 1, we can use dimensional analysis to solve this problem. As you read the question, you can write the equation down as,

?_Na = 10.0g_Na

should suffice. The conversion of 1 amu is 1.660539 x 10^-24 g.

$?_{N a} = 10.0 g_{N a} (\frac{1 a m u}{1.660539 \times 10^{- 24} g}) (\frac{1_{N a}}{22.99 a m u}) = 0.2619 \times 10^{24} N a$

That's a huge number!

Moles

Remember the first example in this chapter? In a 17 g of ammonia, there are always 14 g of nitrogen and 3 g of hydrogen? Can we standardize the mass in terms of gram quantity because gram is the quatity we can directly measure? As amu is defined using C-12 as fundamental unit (for one atom) of mass, we can express atomic mass in grams in the macroscopic scale. For this we need to know the quantity (or number), for example, of nitrogen in 14 g.

We define Avogadro's number to be the number of C-12 atoms present in an exactly 12.0 g of C-12, and is 6.022 x 10²³. This comes straight from the 1 amu = 1.660539 x 10^-24g (Take the recipical of the number associated with g).

It is nuissance to write such a large number all the time: we must express 12.0g/6.022x10²³ C-12. So we make this number into another unit; we call it a mole, abbreviated as mol. Therefore, 1 mol of substance always contains 6.022 x 10²³ substances.

So, C-12 contains 6.022 x 10²³ atoms, which is a mole of C-12.

Example: How many atoms are there in 12.0 g of N-15 and in 15.0 g of N-15?

We can solve this by dimensional analysis. One of the key conversion factors is relating C-12 to N-14. $?_{N - 15} = 12.0 g_{N} (\frac{1 a m u}{1.660539 \times 10^{- 24} g}) (\frac{1_{N - 15}}{15 a m u}) = 0.4818 \times 10^{24} = 4.818 \times 10_{N - 15}^{23}$ $?_{N - 15} = 15.0 g_{N} (\frac{1 a m u}{1.660539 \times 10^{- 24} g}) (\frac{1_{N - 15}}{15 a m u}) = 0.6022 \times 10^{24} = 6.022 \times 10_{N - 15}^{23}$ The number of atoms in 12 g N-15 is less than Avogadro's number—in C-12, however, it gives you Avogadro's number. For 15 g of N-15, the number of N-15 is the same as Avogadro's number. Hence, when the atomic mass in amu is the same as the gram quantity, you have 1 mol.

C-12 → 12 amu → 12 g → Avogadro's number → 1 mol

N-15 → 15 amu → 15 g → Avogadro's number → 1 mol

Average Mass

The average mass comes from averaging over all isotopic masses.

(Isotope = has the same # of protons, but differing in # of neutrons)

〈 m 〉 = c_{1} m_{1} + c_{2} m_{2} + c_{3} m_{3} + c_{4} m_{4} + \dots

Here the <m> is the average mass, and c₁ is the fractional abundance of isotope 1 with the mass, m₁, etc.

If you add all the c₁ + c₂ + c₃ + c₄ + … = 1

Here an easy example of average mass calculation.

Example: Copper has two naturally occuring isotopes. Cu-63 with its mass = 62.94 amu and its abundance = 69.17%, and Cu-65 with its mass = 64.93 amu and its abundance = 30.83%. What is the average mass in amu?

We have,

< m > = c₆₃m₆₃ + c₆₅m₆₅

to which we know all terms on the right-hand side of the equation. Only thing you need to worry about is the abundance expressed in percentage. The fractional abundance is obtained by diving the % by 100. Then,

< m > = (0.6917)(62.94 amu) + (0.3083)(64.93 amu) = 63.55 amu

Above is rather too easy. What about the following?

Example: Copper has two naturally occuring isotopes. Cu-63 with its mass = 62.94 amu and Cu-65 with its mass = 64.93 amu. If the average mass of copper is 63.55 amu, what are the natural abundances in percentage of each isotope?

This time, there are two unknowns, both the c₆₃ and c₆₅. One equation with two unkowns can not be solved. Nonetheless, we have again

< m > = c₆₃m₆₃ + c₆₅m₆₅
but we also have
c₆₃ + c₆₅ = 1

Using this, we now have two equations with two unknowns. This is solvable. We can rearrange the second equation above to sove for c₆₃, then substitute the c₆₃ equation into the average mass equation (1^st eqn) to obtain

$c_{65} = \frac{〈 m 〉 - m_{63}}{m_{65} - m_{63}}$

+ If you want to know how it is derived, click here.

Starting with $〈 m 〉 = c_{63} m_{63} + c_{65} m_{65}$

and we know that

$c_{63} + c_{65} = 1$

Rearranging above, we get

$c_{63} = 1 - c_{65}$

Substituting above into the average mass equation,

$〈 m 〉 = (1 - c_{65}) m_{63} + c_{65} m_{65}$

Then, distribute.

$〈 m 〉 = m_{63} - c_{65} m_{63} + c_{65} m_{65}$

Rearragne to obtain, $〈 m 〉 - m_{63} = c_{65} (m_{65} - m_{63})$

Then finally, solve for c₆₅, $c_{65} = \frac{〈 m 〉 - m_{63}}{m_{65} - m_{63}}$

Once you get the c₆₅ isolated, you can put all the numbers in. Then, you get, $c_{65} = \frac{〈 m 〉 - m_{63}}{m_{65} - m_{63}} = \frac{63.55 a m u - 62.94 a m u}{64.93 a m u - 62.94 a m u} = 0.3065$

Therefore, c₆₅ = 30.65%. Then, c₆₃ = 69.35%. Comparing with the example above, the answer is reasonable.

Molar Mass

So the mystery of where the fraction in the average mass came from, is solved. Let's go back to mole quantity. The average mass listed on the Periodic Table, in the case of Xe, was 131.30 amu. It is much more covenient for us to express this in macroscopic quantity. The mole and amu are defined through C-12, 12 g is 1 mol, and we saw above that 15 g of 15 amu N-15 gives you 1 mol. Therefore, atomic mass in amu gives the equivalent number in g, and always gives the Avogadro's number amount. The average mass works exactly the same way. The average mass of Xe is 131.30 amu, therefore in 131.30 g gives 1 mole. This is called molar mass of element. The unit is g/mol.

Example: What are the molar masses of He, Ca, and Cu?

Just look at the Periodic Table and read off the average masses. For He, it is 4.003, therefore 4.003 g/mol. For Ca, it is 40.078, therefore 40.078 g/mol. Cu = 63.546 g/mol.

Molar Mass of Molecules

The average masses of atoms on the periodic table give the grams of element in one mole of that element. We call it, molar mass of element.

For molecules, molar mass, denoted as μ (mu of Greek character), is given as the total mass of the molecule in one mole of that molecule. Therefore, for water molecule,

μ_H2O = 2m_H + m_O

Example: Molar mass of water:

Not much more complicated example...

Example: Molar mass of Prussian Blue (indigo dye):

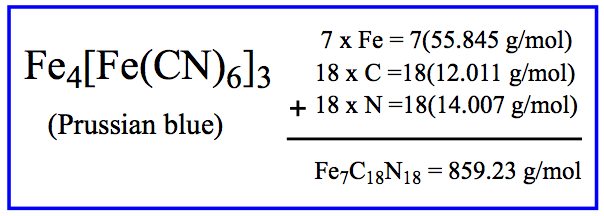
Chemical Calculations

Now you're in the position to perform chemical calculations. For this purpose, we follow dimensional analysis! What's important here is that when comparing two chemical species, you must use stoichiometry, and hence you need to have the balanced chemical equation.

Let's start simple.

Example: a) How many moles are there in a 10.00g of CO₂? b) How many g are there in a 10.0 mol of CO₂?

The molar mass of CO₂ is 44.01 g/mol. So, we ask: a) for calculating the number of moles is $? m o l_{C O 2} = 10.00 g_{C O 2} (\frac{1 {m o l}_{C O 2}}{44.01 g_{C O 2}}) = 0.227221086 {m o l}_{C O 2} = 0.2272 {m o l}_{C O 2}$

The second part is similar.

$? g_{C O 2} = 10.0 {m o l}_{C O 2} (\frac{44.01 g_{C O 2}}{1 {m o l}_{C O 2}}) = 440.1 g_{C O 2} = 440 g_{C O 2}$

Comparison b/w molecules → Use stoichiometry

g to mol and mol to g → always done with the molar mass

Percent Composition

Percent composition of elements in a molecule: We can use % by mass to obtain the percentage of elements in compounds.

In water, 11.19% is H, and 88.81 is O. It then means that for a 100 g of H₂O, there are 11.19 g H and 88.81 g O.

Example: Mass Percent

What is the mass % composition of H and O in H₂O?

Since there are 2 mol H and 1 mol O for 1 mol of H₂ with m = 18.01528 g/mol $\begin{array}{l} %_{H} = \frac{2 (1.008 g / m o l)}{18.01528 g / m o l} \times 100 % = 11.19 % \\ %_{O} = \frac{15.9994 g / m o l}{18.01528 g / m o l} \times 100 % = 88.81 % \end{array}$

Example: Empirical formula from % composition

Using the above % for H₂O, obtain simplest formula (empirical formula).

So, in 100 g H₂O, there are 88.81 g O and 11.19 g H. Since the chemical formula canb be thought as the numerical mole ratio of elements. Let's convert the mass of each element to # of moles.

$\begin{array}{l} ? m o l_{O} = 88.81 g_{O} (\frac{1 m o l_{O}}{15.9994 g_{O}}) = 5.55083 m o l_{O} \\ ? m o l_{H} = 11.19 g_{H} (\frac{1 m o l_{H}}{1.0079 g_{H}}) = 11.10185 m o l_{H} \end{array}$

Molecular formula is simple numerical ratio between elements in molecules. So, 11 mol H to 5.6 mol O reduces to 2 mol H and 1 mol O. This is why water has formula H₂O. $H_{11.10185} O_{5.55083} \to H_{\frac{11.10185}{5.55083}} O_{\frac{5.55083}{5.55083}} = H_{2.00003} O_{1} = H_{2} O$

Basically, by writing down the number of moles calculated from % composition for each element, then divide the numbers by the smallest value of moles. Here the important thing it to calculate the number of moles from %.

Chemical Rxn

Chemical reaction is represented by chemical equation, which separates reactant(s), which is starting material(s), to products(s), which is end result(s) of the reaction, by using an arrow (→), representing the direction to which the reaction proceeds.

This is often referred to as forward reaction. There is reverse reaction, for which the arrow is reversed(←), and product is converted to reactant. Yet another one, having two arrows pointing opposite ways and placed on top of each other (⇄), symbolizes the conditioin called equilibrium (topic covered in Chapter 11 and much of CHM4).

Example: Given the following chemcial equation, calculate various quatities.

P₄ + 6Cl₂ → 4PCl₃

Let's start with:
How many moles of Cl₂ do you need to obtain 2 moles of PCl₃?

$? m o l_{C l_{2}} = 2.0 m o l_{P C l_{3}} (\frac{6 m o l_{C l_{2}}}{4 m o l_{P C l_{3}}}) = 3.0 m o l_{C l_{2}}$

How many moles of PCl₃ can it be obtained if you have 2.0 mol of P₄?

$? m o l_{P C l_{3}} = 2.0 m o l_{P_{4}} (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) = 8.0 m o l_{P C l_{3}}$

If you have 2.00 g of P₄, how many mole of PCl₃ can it be obtained?

$? m o l_{P C l_{3}} = 2.00 g_{P_{4}} (\frac{1 m o l_{P_{4}}}{123.895 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) = 0.06457080 m o l_{P C l_{3}} = 0.0646 m o l_{P C l_{3}}$

If you have 2.00 g of P₄, how many grams of PCl₃ can it be obtained? $? g_{P C l_{3}} = 2.00 g_{P_{4}} (\frac{1 m o l_{P_{4}}}{123.895 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) (\frac{137.33 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 8.867509 g_{P C l_{3}} = 8.87 g_{P C l_{3}}$

So, above examples shows the complexity of converting grams of cetrain reactant to grams of certain product is easily calculated.

Experimental Determination of Empirical Formula

Using the procedure to obtain empirical formula from % composition, we can work out the so-called combustion analysis. Combustion of hydrocarbon, species that contains only C and H, is a process where the hyrdocarbon molecules react with O₂ to produce carbon dioxide and water.

C_xH_y + O₂ → xCO₂ + (y/2)H₂O

So, if you know the amount of CO₂ and H₂O produced in the combustion process, we can calculate the values of x and y, and therefore we can obtain empirical formula of the reactant.

Example: Combustion Analysis

Combustion of hydrocarbon produced 33.01 g CO₂ and 13.51 g H₂O. What is the empirical formula of the hydrocarbon?

From equation above, the number of moles of C in CO₂ came from C_xH_y, so as the number of moles of H in H₂O. If we covert the mass of CO₂ to mol of C, and the mass of H₂O to mol of H, we can obtain the empirical formula for the hydrocarbon.

$\begin{array}{l} ? m o l_{C} = 33.01 g_{C O_{2}} (\frac{1 m o l_{C O_{2}}}{44.0095 g_{C O_{2}}}) (\frac{1 m o l_{C}}{1 m o l_{C O_{2}}}) = 0.750 m o l_{C} \\ ? m o l_{H} = 13.51 g_{H_{2} O} (\frac{1 m o l_{H_{2} O}}{18.01528 g_{H_{2} O}}) (\frac{2 m o l_{H}}{1 m o l_{H_{2} O}}) = 1.50 m o l_{H} \end{array}$

Above calculations show C_0.750H_1.50, and yields CH₂ by dividing both numbers by 0.750.

Example: Combustion Analysis #2

A 12.01 g tartaric acid contains C, H, and O. Upon combustion, 14.08 g CO₂ and 4.32 g H₂O are produced. Deduce the empirical formula.

Now we have added complication of having O in the compound. Oxygen can come from O₂ and these oxygen becomes distributed into CO₂ and H₂O, so we must determine the mass of O in the sample somehow.

The way to calculate the mass of O in the sample is to calculate the masses of C and H and subtracted from the total sample mass (12.01 g). Then, you have the mass of oxygen from the original sample.

$\begin{array}{l} ? g_{C} = 14.08 g_{C O_{2}} (\frac{1 m o l_{C O_{2}}}{44.0095 g_{C O_{2}}}) (\frac{1 m o l_{C}}{1 m o l_{C O_{2}}}) (\frac{12.0107 g_{C}}{1 m o l_{C}}) = 3.84259 g_{C} \\ ? g_{H} = 4.32 g_{H_{2} O} (\frac{1 m o l_{H_{2} O}}{18.01528 g_{H_{2} O}}) (\frac{2 m o l_{H}}{1 m o l_{H_{2} O}}) (\frac{1.00794 g_{H}}{1 m o l_{H}}) = 0.48340 g_{H} \end{array}$ $12.01 g - 3.84259 g_{C} - 0.48340 g_{H} = 7.684 g_{O}$

$\begin{array}{l} ? m o l_{C} = 14.08 g_{C O_{2}} (\frac{1 m o l_{C O_{2}}}{44.0095 g_{C O_{2}}}) (\frac{1 m o l_{C}}{1 m o l_{C O_{2}}}) = 0.31993 m o l_{C} \\ ? m o l_{H} = 4.32 g_{H_{2} O} (\frac{1 m o l_{H_{2} O}}{18.01528 g_{H_{2} O}}) (\frac{2 m o l_{H}}{1 m o l_{H_{2} O}}) = 0.47959 m o l_{H} \\ ? m o l_{O} = 7.684 g_{O} (\frac{1 m o l_{O}}{15.9994 g_{O}}) = 0.48027 m o l_{O} \end{array}$ $C_{0.31993} H_{0.47959} O_{0.48027} = C_{1} H_{1.49905} O_{1.50117} = C_{2} H_{3} O_{3}$

If one calculates the molar mass for the empirical formula, you get 74.046 g/mol. The actual molar mass of tartaric acid is 148.092 g/mol. Therefore, if the empirical formula is multiplied by two, one gets the correct formula.

Balancing Chemical Equation

Chemical Equation
Chemical equation shows the transformation of molecules starting with the reactants, the left-hand side of the equation, and ending in products on the right-hand side. The arrow separates the reactants from the products. Below is an example of a reaction for water molecules transformed into hydrogen molecules and oxygen molecules.

From the point of view of Conservation of Mass, it stands to reason that all atoms present in the reactants have to be present in the products.

m_reactants = m_products

There are 4 hydrogen atoms and 2 oxygen atoms on the left-hand side.

There are 4 hydrogen atoms and 2 oxygen atoms on the right-hand side.

When the chemical equation satisfys mass conservation, it is said to be balanced.

Balancing
Some tips upon balancing chemical eqns.

Do more complicated molecules first

Leave homonuclear diatomic molecules and other simpler molecules to the end

Example: Balance the following:

Al + S → Al₂S₃

Since on the right-hand side, there are two Al and three S atoms, the left-hand side must have respectively the same Al and S atoms. So,

2Al + 3S → Al₂S₃

Too easy? What about next one?

Example: Balance the following:

C₂H₈N₂ + N₂O₄ → N₂ + CO₂ + H₂O

Step by step.

First to match the number of C

C₂H₈N₂ + N₂O₄ → N₂ + 2CO₂ + H₂O

We need at least 8 H, so

C₂H₈N₂ + N₂O₄ → N₂ + 2CO₂ + 4H₂O

By doing above, you realize you have 8 oxygen on the right-hand side, but only 4 on the left, so

C₂H₈N₂ + 2N₂O₄ → N₂ + 2CO₂ + 4H₂O

Finally, adjust N by,

C₂H₈N₂ + 2N₂O₄ → 3N₂ + 2CO₂ + 4H₂O

However I explain it, you have to practice to get a hung of it!

Stoichiometry

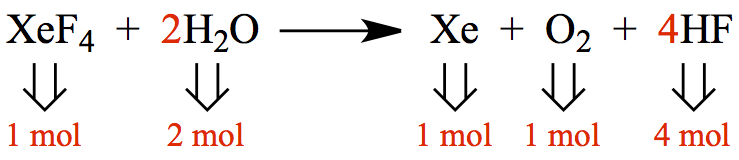
Consider the following:

XeF₄ + 2H₂O → Xe + O₂ + 4HF

We can pictorially represent above chemical eqn as,

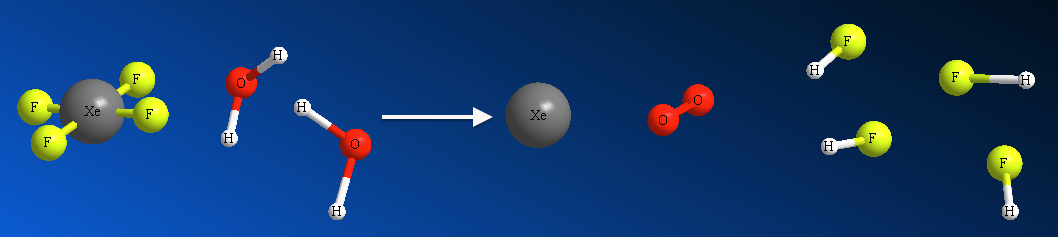
This is a microscopic view with each of the molecules in the reaction are shown.

How should we represent this microscopic knowledge onto the macroscopic view? What I mean by is, say, you are asked to calculate the gram quantity of XeF₄ to make 10.0 g of HF. Now, it is no longer a single-molecule picture. Remember that a mere 18.0 g of water contains 6.022 x 10²³ molecules!!??, i.e. 602 200 000 000 000 000 000 000 of them!!!!

For macroscopic quantities, we define mole, abbreviated as mol.

Definition: There are 6.022 x 10²³ ¹²C atoms in exactly 12.00 g of ¹²C.

It means that there are 12.011 g of naturally occuring carbon, containing different isotopes. It means that the average masses of the elements on the Periodic Table are the masses of each element in 1 mol of that element.

Therefore, the number of molecules in the microscopic picture also corresponds to the amount of moles of each molecules. The coefficients in front of chemical formula are so-called stoichiometric coefficients. They represent the number of moles!

Yield of Product

Acutal vs. Theoretical Yields

The amount of product actually produced is called yield (or actual yield). Since the reaction of interest may have other pathways so that the the product may not form as much as it should, or even your filteration system may have reduced your products. So, the actual yield may be lower than the theoretically possible amount of product. The theoretical yield is the maximum amount allowed by the stoichiometry.

Percent Yield

$%_{y i e l d} = \frac{g_{a c t u a l}}{g_{t h e o r e t i c a l}} \times 100 %$

Example: % yield of reaction:

Given the following reaction.

P₄ + 6Cl₂ → 4PCl₃ If there was 6.44 g of PCl₃ produced from 2.00 g of P₄, what is the % yield?

$? g_{P C l_{3}} = 2.00 g_{P_{4}} (\frac{1 m o l_{P_{4}}}{123.895 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) (\frac{137.33 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 6.578473 g_{P C l_{3}} = 6.58 g_{P C l_{3}}$ $%_{y i e l d} = \frac{6.44 g}{6.58 g} \times 100 % = 97.8723 % = 97.9 %$

%_yield can be used as the conversion factor in the dimensional analysis!

It means that some # of g_{something actual} = 100 g_{something theoretical}

Limiting Reactant

Here is a recipe for pizza:

Item	Qty
Dough	1
Tomato sauce	5 oz
Cheese	2 cups

So, if you have above quantity of items, you can make a pizza. If you have two doughs, but you still have a 5-oz tomato sauce, and 4 cups of cheese, how many complete pizza can you make? Obviously only one still, because of the 5 oz tomato sauce. In chemical terms, the equivalent of tomato sauce here is what we call limiting reactant, and this yield only one pizza.

Example: Limiting Reactant: What is the mass of PCl₃ formed from 125 g of P₄ and 323 g of Cl₂ in the following reaction?

P₄ + 6Cl₂ → 4PCl₃

$\begin{array}{l} ? g_{P C l_{3}} = 125 g_{P_{4}} (\frac{1 m o l_{P_{4}}}{123.9 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) (\frac{137.3 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 554 g_{P C l_{3}} \\ ? g_{P C l_{3}} = 323 g_{C l_{2}} (\frac{1 m o l_{C l_{2}}}{70.91 g_{C l_{4}}}) (\frac{4 m o l_{P C l_{3}}}{6 m o l_{C l_{2}}}) (\frac{137.3 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 417 g_{P C l_{3}} \end{array}$

Therefore, Cl₂ yields smaller quantity of product. Hence, Cl₂ is the limiting reactant, yielding 417 g.

Chapter 3 Mass Relationships in Chemical Rxns

Intro to chemical calculations

Moles

Molar Mass