Chapter 1 Matter and Measurement

Example:1.85 The density of silver is 10.5 g/cm³. What is the mass in kg of a cube of silver that measures 0.62 m on each side?

The volume of the cube is (0.62 m)³. The question is how many kg are there in (0.62 m)³? $? k g = {(0.62 m)}^{3} {(\frac{10^{2} c m}{1 m})}^{3} (\frac{10.5 g}{1 c m^{3}}) (\frac{1 k g}{10^{3} g}) = 2.502444 \times 10^{3} k g = 2.5 \times 10^{3} k g$

Example:1.52 Carry out the following conversions:
a. 5 pm = __ cm = __ nm
b. 8.5 cm³ = __ m³ = __ mm³

a. Ask, how many cm are there in 5 pm? $? c m = 5 p m (\frac{1 m}{10^{12} p m}) (\frac{10^{2} c m}{1 m}) = 5 \times 10^{- 10} c m$ Similarly, $? n m = 5 p m (\frac{1 m}{10^{12} p m}) (\frac{10^{9} n m}{1 m}) = 5 \times 10^{- 3} n m$

b. Little tricky. But, the similar question, how many m³ are there in 8.5 cm³? $? m^{3} = 8.5 c m^{3} {(\frac{1 m}{10^{2} c m})}^{3} = 8.5 \times 10^{- 6} m^{3}$ Notice we're cubing the whole parenthesis!! Then, we can do the second part, as well. $? m m^{3} = 8.5 c m^{3} {(\frac{1 m}{10^{2} c m})}^{3} {(\frac{10^{3} m m}{1 m})}^{3} = 8.5 \times 10^{3} m m^{3}$

Example:1.96 When an irregularly shaped chunk of silicon weighing 8.763 g was placed in a graduated cylinder containing 25.00 mL of water, the water level in the cylinder rose to 28.76 mL. What is the density of silicon in g/cm³?

Since $d = \frac{m}{V}$ The volume of silicon is given by the difference of the water levels before and after placing the silicon in, which is 3.76 mL. $d = \frac{8.763 g}{3.76 m L} = 2.330585 g / m L = 2.33 g / c m^{3}$ The conversion factor 1 mL = 1 cm³ is used in the last equality.

Example:1.105 Vinaigrette salad dressing consists mainly of oil and vinegar. The density of olive oil is 0.918 g/cm³, the density of vinegar is 1.006 g/cm³, and the two do not mix. If a certain mixture of olive oil and vinegar has a total mass of 397.8 g and a total volume of 422.8 cm³, what is the volume of oil and what is the volume of vninegar in the mixture?

+ Can you summerize the question in terms of a diagram? Also, what is the essence of the question?

The question can be summarized as follows.

We know the total volume and its components are $V_{t o t a l} = V_{o i l} + V_{v i n}$ Similarly, the total mass and its components are $m_{t o t a l} = m_{o i l} + m_{v i n}$

+ Before you look at the answer, please think about the problem!

But, the mass is related to the volume by density, since density is mass/volume. Then, we can write the total mass to be

m_{t o t a l} = d_{o i l} V_{o i l} + d_{v i n} V_{v i n}

If we solve for V_oil for the total volume equation above,

V_{o i l} = V_{t o t a l} - V_{v i n}

If we substitute above into the total mass, we have

m_{t o t a l} = d_{o i l} (V_{t o t a l} - V_{v i n}) + d_{v i n} V_{v i n}

Now, as you can see that only unknown we have in the equation above is V_vin. Let's solve for that.

m_{t o t a l} = d_{o i l} (V_{t o t a l} - V_{v i n}) + d_{v i n} V_{v i n}

m_{t o t a l} = d_{o i l} V_{t o t a l} - d_{o i l} V_{v i n} + d_{v i n} V_{v i n}

m_{t o t a l} = d_{o i l} V_{t o t a l} + V_{v i n} (d_{v i n} - d_{o i l})

m_{t o t a l} - d_{o i l} V_{t o t a l} = V_{v i n} (d_{v i n} - d_{o i l})

And, finally,

V_{v i n} = \frac{m_{t o t a l} - d_{o i l} V_{t o t a l}}{(d_{v i n} - d_{o i l})}

Place all the values in, then

V_{v i n} = \frac{397.8 g - (0.918 g / c m^{3} \cdot 422.8 c m^{3})}{1.006 g / c m^{3} - 0.918 g / c m^{3}} = \frac{9.6696 g}{0.088 g / c m^{3}}

The volume of vinegar then is

V_{v i n} = 109.8818 c m^{3} = 110 c m^{3}

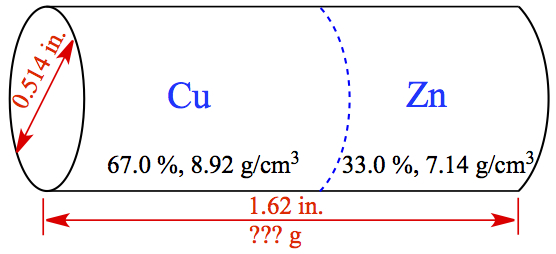
Therefore, the volume of oil then is $V_{o i l} = V_{t o t a l} - V_{v i n} = 442.8 c m^{3} - 110 c m^{3} = 313 c m^{3}$

Example:1.112 Brass is a copper-zinc alloy. What is the mass in grams of a brass cylinder having a length of 1.62 in. and a diameter of 0.514 in. if the composition of the brass is 67.0 % copper and 33.0 % zinc by mass? The density of copper is 8.92 g/cm³, and the density of zinc is 7.14 g/cm³. Assume that the density of the brass varies linearly with composition.

+ Summerize the question in a diagram, and think about what's given and how you might approach it.

This is a difficult one. Although in reality brass is completely a uniform mixture of Cu and Zn, and one can not separate them, we picture the two component to be separable.

So, we are looking for the total mass of the alloy. From the picture, you can see that if the mass of Cu and the mass of Zn are calculated, we have the mass of the alloy. It means, $m_{a l l o y} = m_{C u} + m_{Z n}$

The mass of copper and the mass of zinc are related to the mass of alloy by the percentage. From the definition of % by mass, we know that $\begin{array}{l} m_{C u} = 0.67 m_{a l l o y} \\ m_{Z n} = 0.33 m_{a l l o y} \end{array}$

We also have the total volume of alloy, $V = π r^{2} l$ where r is the radius of the circular face and l is the length. $? c m = 0.257 i n (\frac{2.54 c m}{1 i n}) = 0.65278 c m$ $? c m = 1.62 i n (\frac{2.54 c m}{1 i n}) = 4.1148 c m$ $V_{a l l o y} = π {(0.65278 c m)}^{2} (4.1148 c m) = 5.50849 c m^{3}$

+ Click here to see the answer.

The volume of alloy, for which we have now a numerical value, should be examined further. We know that there are two contribution, one from Cu and one from Zn.

V_{a l l o y} = V_{c u} + V_{Z n}

Since d = m/V, we can rearrange to have V=m/d. Then,

V_{a l l o y} = \frac{m_{C u}}{d_{C u}} + \frac{m_{Z n}}{d_{Z n}}

We also know that in this alloy the mass of Cu is 67% of total mass, as well as the mass of Zn is 33% of total mass. Then, the above equation is

V_{a l l o y} = \frac{0.67 m_{a l l o y}}{d_{C u}} + \frac{0.33 m_{a l l o y}}{d_{Z n}}

As you can see, only unknown in the equation is m_alloy. Let's now solve for m_alloy. Let's multiply first and the second terms of the right-hand side of the quation by, respectively, d_Zn/d_Zn and d_Cu/d_Cu. (Effectively, you are multiplying 1 to both terms!)

V_{a l l o y} = \frac{0.67 m_{a l l o y} d_{Z n}}{d_{C u} d_{Z n}} + \frac{0.33 m_{a l l o y} d_{C u}}{d_{Z n} d_{C u}}

V_{a l l o y} = \frac{m_{a l l o y} (0.67 d_{Z n} + 033 d_{C u})}{d_{C u} d_{Z n}}

d_{C u} d_{Z n} V_{a l l o y} = m_{a l l o y} (0.67 d_{Z n} + 033 d_{C u})

m_{a l l o y} = \frac{d_{C u} d_{Z n} V_{a l l o y}}{0.67 d_{Z n} + 033 d_{C u}}

m_{a l l o y} = \frac{(8.92 g / c m^{3}) (7.14 g / c m^{3}) (5.50849 c m^{3})}{0.67 (7.14 g / c m^{3}) + 0.33 (8.92 g / c m^{3})} = \frac{350.829118 g^{2} / c m^{3}}{7.7274 g / c m^{3}} = 45.4 g

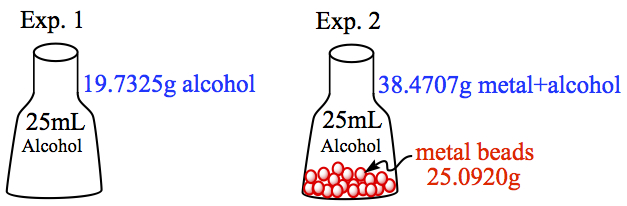
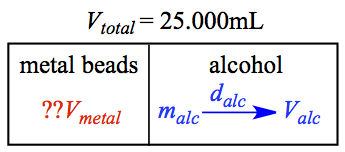
Example: A calibrated pycnometer with its volume 25.000 mL was filled with ethyl alcohol. By weighing the flask before and after adding the alcohol, it was determined that the pycnometer contains 19.7325 g of alcohol. In a second experiment, a 25.0920 g of metal beads were added to the pycnometer and the pycnometer was filled with alcohol to 25.000 mL mark. The total mass of the metal beads and alcohol in the pycnometer was deternined to be 38.4704 g. What is the density of the metal beads in g/mL?

+ Diagram the question.

The two experiments are depicted as follows.

In the first experiment (Exp. 1) shows the volume of pycnometer and the mass of alcohol in the pycnometer. Can you see that you can calculate the density of alcohol?

In the second experiment, we have the mass of the metal beads, and the combined mass of metal and alcohol. Of course, the volume of the pycnometer stays the same. In order to calculate the density of the metal beads, we need to know the mass and volume of the metal. $d_{m e t a l} = \frac{m_{m e t a l}}{V_{m e t a l}}$ We know the mass of the metal, 25.0920 g. So, we are looking for the volume of the metal beads. Let's visualize the volume inside the pycnometer as follows.

+ Here is the answer.

The total volume of 25 mL is composed of metal beads part and alcohol part. If we know the volume of alcohol, we can subtract the amount of alcohol from the total to get the volume of the metal beads. We can calculate the mass of alcohol, and it can be converted to the volume by knowing the density of alcohol. Experiment 1 provides the density.

m_alc = 38.4707 g − 25.0920 g = 13.3787 g

$? m L_{a l c} = 13.3787 g (\frac{25.000 m L}{19.7325 g}) = 16.9501 m L$

V_metal = 25.000 mL − 16.9501 mL = 8.050 mL

Then, the density of metal beads is then $d_{m e t a l} = \frac{25.0920 g}{8.050 m L} = 3.11702 g / m L = 3.117 g / m L$

Example:1.100. A graduated cylinder is filled to the 40.00-mL mark with a mineral oil. The masses of the cylinder before and after the addition of the oil are 124.966g and 159.446g, respectively. In a separate experiment, a metal ball (sphere) of mass 18.713g is placed in the cylinder and the cylinder is filled again to the 40.00-mL mark with the mineral oil. The combined mass of the ball and oil is 50.952g. Calculate the density and radius of the metal ball. The volume of sphere of radius r is (4/3)πr³.

This is nearly the same question as above! Do you see?

Example: What is the length of a 10-lb spool of 12 gauge aluminum wire? A 12 gauge has a diameter of 0.0808 in. and the density of aluminum is 2.70 g/cm³.

We can visualize the question by unfolding the spool and straighten the wire to a cylindrical form as follows.

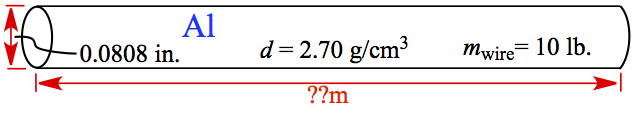
The volume of cylinder is given by $V = π r^{2} l$ where r is the radius of the circular face, and l is the length in question. Solving for l, we have $l = \frac{V}{π r^{2}}$ Let's calculate the volume first. Since the length we want is in m, the volume we calculate should be in m³; so this is what we're looking for. What is our given? The given should be 10 lb. 12 gauge and 0.0808 in. are measures of diameter, which relates to r. So, only option is 10 lb. We ask, how many m³ are there in 10 lb.? $? m^{3} = 10 l b (\frac{453.6 g}{1 l b}) (\frac{c m^{3}}{2.70 g}) {(\frac{1 m}{100 c m})}^{3} = 1.67999 \times 10^{- 3} m^{3}$ For r we need the value in m. The radius of the circular area is 0.0404 in. So, $? m = 0.0404 i n (\frac{2.54 c m}{1 i n}) (\frac{1 m}{100 c m}) = 1.02616 \times 10^{- 3} m$ Substitute the numbers into l = V /(πr²), we get. $l = \frac{1.67999 \times 10^{- 3} m^{3}}{π {(1.02616 \times 10^{- 3} m)}^{2}} = \frac{1.67999 \times 10^{- 3} m^{3}}{3.30811 \times 10^{- 6} m^{2}} = 507.842 m = 508 m$

Example: One acre-ft is defined as a volume of an acre of land filled with water to a depth of one foot. What is 1 acre-ft in ft³? and in m³, given that 640 acre = 1 mi², 1 mi = 1.609344 km, 1 in. = 2.54 cm, and 12 in. = 1 ft?

The pictorial representation of the question is as follows.

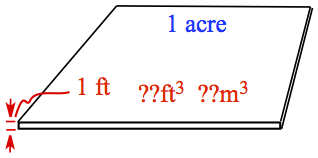
We want to know the volume of acre-ft in, first, ft³. If we convert the area of 1 acre in ft², the volume is obtained by multiplying 1 ft at the end, so our question is, how many ft² are there in 1 acre? $? f t^{2} = 1 a c r e (\frac{1 m i^{2}}{640 a c r e}) {(\frac{1.609344 k m}{1 m i})}^{2} {(\frac{10^{3} m}{1 k m})}^{2} {(\frac{10^{2} c m}{1 m})}^{2} {(\frac{1 i n}{2.54 c m})}^{2} {(\frac{1 f t}{12 i n})}^{2}$ $? f t^{2} = 43560 f t^{2} = 4.36 \times 10^{4} f t^{2} \to 4.36 \times 10^{4} f t^{3}$ The last arrow indicates that the height of 1 ft is multipled to get the volume.

Let's calculate now the volume in m³. $? m^{3} = 43560 f t^{3} {(\frac{12 i n}{1 f t})}^{3} {(\frac{2.54 c m}{1 i n})}^{3} {(\frac{1 m}{10^{2} c m})}^{3} = 1233.412 m^{3} = 1.23 \times 10^{3} m^{3}$

Example: Taken from the Prelab question: What is the volume of a room in L that hold 30.0 kg of oxygen (O₂), if the density of O₂ is 1.300 g/L, and oxygen in air is 21.0 % by volume?

The pictorial representation of the problem is

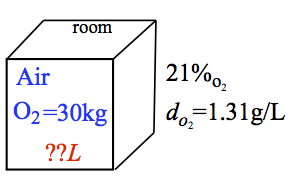
The key is to understand what each of the givens and what we are looking for. First, we are looking for the volume of the room. There seems to be no conversion factor that relates O₂ to the room. But, air does relate to O₂. So, instead of asking for the volume of the room, we are asking for the volume of air. Density is a conversion factor converting mass to volume or vise versa. The percent by volume is also a conversion factor because when expanded, it means that $21 %_{O_{2} (v o l u m e)} = \frac{21 L_{O_{2}}}{100 L_{a i r}} \times 100 %$ So, we use the ratio of 21 L_O₂ / 100 L_air as the conversion factor. It must mean that the 30.0 kg is our given, so that we ask, "How many L of air that contains a 30 kg of O₂?" Then, $? L_{a i r} = 30.0 k g_{O_{2}} (\frac{10^{3} g_{O_{2}}}{1 k g_{O_{2}}}) (\frac{1 L_{O_{2}}}{1.31 g_{O_{2}}}) (\frac{100 L_{a i r}}{21.0 L_{O_{2}}}) = 1.0905125 \times 10^{5} L_{a i r} = 1.09 \times 10^{5} L_{a i r}$

Example: 1.93 Sodium (Na) metal undergoes a chemical reaction with chlorine (Cl) gas to yield sodium chloride, table salt. If 1.00 g of sodium reacts with 1.54 g of chlorine, 2.54 g of sodium chloride is formed, 17.9 kJ of heat is released. How much sodium and how much chlorine in grams would have react to release 171 kcal of heat

Pictorially, you have

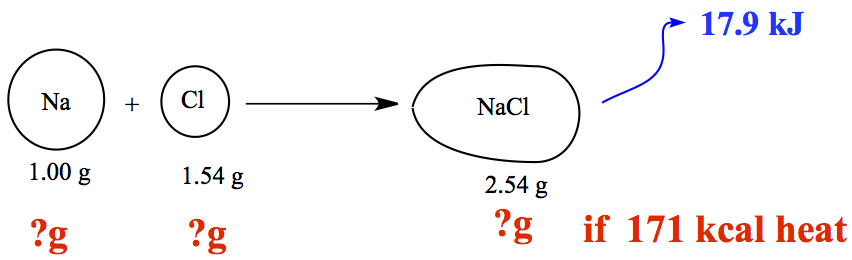
You can see that 17.9 kJ of heat generated per 1.00 g Na. So, we can use 17.9 kJ/g_Na as a conversion factor. We ask, $? g_{N a} = 171 k c a l (\frac{1000 c a l}{1 k c a l}) (\frac{4.184 J}{1 c a;}) (\frac{1 k J}{1000 J}) (\frac{1.00 g_{N a}}{17.9 k J}) = 39.970 g_{N a} = 40.0 g_{N a}$

Example: 1.92 Chlorine is used to disinfect swimming pools. The accepted concentration for this purpose is 1 ppm chlorine, or 1 g of chlorine per million g of water. Calculate the volume of a chlorine solution ( in mL) a homeowner should add to her swimming pool if the solution concentration is 6.0 % chlorine by mass and there are 2.0 x 10⁴ gal of water in the pool. 1 gal = 3.79 L density of liquid = 1.0 g / mL

Chapter 1 Matter & Measurement

Units Conversions

Chapter 1 Practice Problems