Chapters 3 and 4. Additional & Practice Problems

Example:How many g of PCl₃ formed from 100 g of Cl₂, if it was reacted with 50.0 g of P₄ according to the following reaction? Also, how many g of P₄ left after the reaction?

P₄ + Cl₂ → PCl₃

First, the chemical eqation is not balanced. So, you need to balance it.

P₄ + 6Cl₂ → 4PCl₃ Since we know the masses of the both reactants, we need to do limiting reactant calculation.

\begin{array}{l} ? g_{P C l_{3}} = 50.0 g_{P_{4}} (\frac{1 m o l_{P_{4}}}{123.9 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{1 m o l_{P_{4}}}) (\frac{137.3 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 222 g_{P C l_{3}} \\ ? g_{P C l_{3}} = 100 g_{C l_{2}} (\frac{1 m o l_{C l_{2}}}{70.91 g_{P_{4}}}) (\frac{4 m o l_{P C l_{3}}}{6 m o l_{C l_{2}}}) (\frac{137.3 g_{P C l_{3}}}{1 m o l_{P C l_{3}}}) = 129 g_{P C l_{3}} \end{array}

Therefore, 129 g of PCl₃ prodced, and Cl₂ is the limiting reactant.

In order for us to calculate the number of g of P₄ left over, we need to know how many g of P₄ used for producing 129 g of PCl₃. So, we say, $? g_{P_{4}} = 129 g_{P C l_{3}}$

Example:1.120 The moecular formula of malonic acid is C₃H₄O₄. If a solution containing 0.762 g of the acid is requires 12.44 mL of 1.174 M NaOH for neutralization, how many ionizable H atoms are present in the molecule?

The situation is that we can calculate the number of moles of H⁺ from the acid reacted by knowing the volume of NaOH with the number of H⁺ available for dissociation from the mass and the chemical formula.

Pictorially,


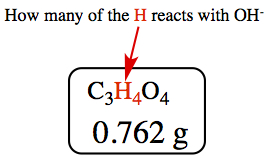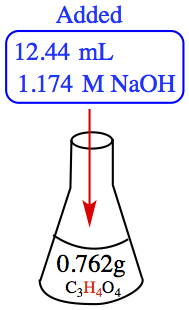We can calculate the number of moles of H available in the molecule, depending on how many of the hydrogens dissociated because we know the molar mass! In principle (at the current chapter), you have up to four H available for dissociation. So, you might need to calculate for four different scenarios!	From this picture, we can calculate the number of moles of H consumued by the OH^- ion.

It means that we need to perform two different set of calculations: from the picture on left to see how many moles of H dissociates depending on the level of dissociation; you have up to four hydrogens, and from the picture on right to see how many moles of H actually dissociated. If the two calculations match in numbers you can tell how many of the H in the molcules dissociated.

If only one H dissociates: $? m o l_{H^{+}} = 0.762 g_{C_{3} H_{4} O_{4}} (\frac{1 m o l_{C_{3} H_{4} O_{4}}}{104.062 g_{C_{3} H_{4} O_{4}}}) (\frac{1 m o l_{H^{+}}}{1 m o l_{C_{3} H_{4} O_{4}}}) = 0.00732256 m o l_{H^{+}} = 7.32 \times 10^{- 3} m o l_{H^{+}}$

If two H dissociate: $? m o l_{H^{+}} = 0.762 g_{C_{3} H_{4} O_{4}} (\frac{1 m o l_{C_{3} H_{4} O_{4}}}{104.062 g_{C_{3} H_{4} O_{4}}}) (\frac{2 m o l_{H^{+}}}{1 m o l_{C_{3} H_{4} O_{4}}}) = 0.01464512 m o l_{H^{+}} = 1.46 \times 10^{- 2} m o l_{H^{+}}$

Just in case, if three H dissociate: $? m o l_{H^{+}} = 0.762 g_{C_{3} H_{4} O_{4}} (\frac{1 m o l_{C_{3} H_{4} O_{4}}}{104.062 g_{C_{3} H_{4} O_{4}}}) (\frac{3 m o l_{H^{+}}}{1 m o l_{C_{3} H_{4} O_{4}}}) = 0.02196767 m o l_{H^{+}} = 2.20 \times 10^{- 2} m o l_{H^{+}}$

Now, the second part: We need to calculate the actual amount of H⁺ dissociated, for which it was neutralized by the OH^- ion. For such calculation, you need to set up dimensional analysis. You ask yourself,

"how many moles of H⁺ does it require to react 12.44 mL of 1.174 M NaOH?"

The [1.174 M] is the molarity, which contains two fundamental units mol and L or 10³mL, thusly molarity is a conversion factor. So, we start our calculation by

?mol_H = 12.44 mL_NaOH Continuing the calculation yields,

? m o l_{H^{+}} = 12.44 m L_{N a O H} (\frac{1.174 m o l_{N a O H}}{10^{3} m L_{N a O H}}) (\frac{1 m o l_{O H^{-}}}{1 m o l_{N a O H}}) (\frac{1 m o l_{H^{+}}}{1 m o l_{O H^{-}}}) = 0.01460456 m o l_{H^{+}} = 1.460 \times 10^{- 2} m o l_{H^{+}}

The value just calculated corresponds to the two H dissoication. Therefore, there are two hydrogens in the molecule avialable for ionization.

Example:1.122 A 60.0 mL 0.513 M glucose (C₆H₁₂O₆) solution is mixed with 120.0 mL of 2.33 M glucose solution. What is the final concentration, if you assume that the volume is additive?

Example: Calculate the concentration of chloride ions in the solution where 200.0 mL of 0.400M NaCl is titrated with the 80.0 mL of 0.750M AgNO₃.

How many g of AgCl is produced by adding 160.0 mL of 0.75M AgNO₃ into 200.0 mL of 0.400M NaCl?

Example:1.127 The molar mass of a certain metal carbonate, MCO₃, can be determined by adding an excess of HCl acid to react with all the carbonate and then "back titrating" the remaining acid with a NaOH solution. (a) Write an equation for these reactions. (b) In a certain experiment, 20.00 mL of 0.0800 M HCl were added to a 0.1022 g sample of MCO₃. The excess HCl required 5.64 mL of 0.1000 M NaOH for neutralization. Calculate the molar mass of the carbonate and identify M.

For simplification, we assume that the metal M of MCO₃ molecule dissoicates into M²⁺ and CO₃^2-. Then, it takes 2 mol H⁺ to make H₂CO₃.

The excess HCl part: Here the assumption is that the H₂CO₃ would not let any of H to dissociates.

The pictorial representation is:

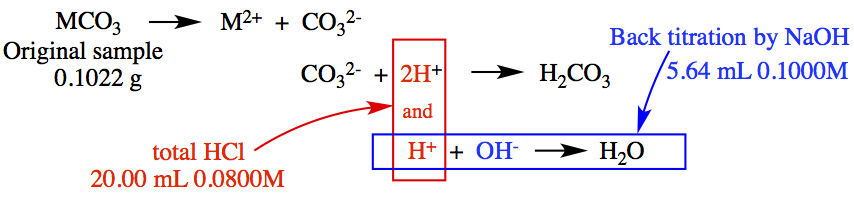
As you can see in the diagram above, there is a sequence of three reactions occur:

1^st line. MCO₃ dissociation

2^nd line. CO₃^2- binds with 2 mol H⁺

3^rd line. Excess H⁺ is neutralized by NaOH

So, the strategy in solving this question is to obtain:

1) the total amount of H⁺ in HCl,

2) the amount of H⁺ used up by NaOH,

3) the amount of H⁺ bound to CO₃^2-,

4) the amount of CO₃^2-,

5) the amount in grams of CO₃^2-,

6) the gram quantity of M²⁺

7) finally calculate molar mass of M²⁺, hence the identity of metal M.

I'm not sure if the following is helpful, but it is pictorial representation of the strategy on how to solve the problem.

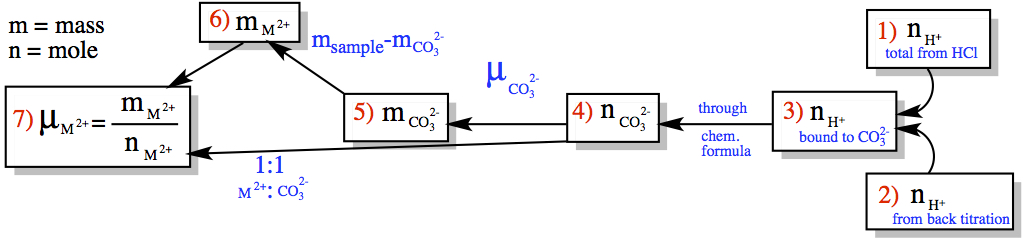
1) The total number of protons from the 0.0800 M HCl solution is $? m o l_{_{H^{+}}}^{t o t a l} = 20.00 m L_{H C l} (\frac{0.0800 m o l_{H C l}}{1000 m L_{H C l}}) (\frac{1 m o l_{H^{+}}}{1 m o l_{H C l}}) = 1.60 \times 10^{- 3} m o l_{H^{+}}$ 2) The amount of H⁺ used up by the back titration using 0.1000 M NaOH is $? m o l_{_{H^{+}}}^{n e u t r a l} = 5.64 m L_{N a O H} (\frac{0.1000 m o l_{N a O H}}{1000 m L_{N a O H}}) (\frac{1 m o l_{O H^{-}}}{1 m o l_{N a O H}}) (\frac{1 m o l_{H^{+}}}{1 m o l_{O H^{-}}}) = 5.64 \times 10^{- 4} m o l_{H^{+}}$ 3) So, if we subtract the amount of H⁺ neutralized from the total amount of H⁺ came from HCl gives the amount of H⁺ bound to CO₃^2-. $? m o l_{_{H^{+}}}^{b o u n d} = m o l_{_{H^{+}}}^{t o t a l} - m o l_{_{H^{+}}}^{n e u t r a l} = 1.60 \times 10^{- 3} m o l_{H^{+}} - 5.64 \times 10^{- 4} m o l_{H^{+}} = 1.04 \times 10^{- 3} m o l_{H^{+}}$ 4) The number of moles of CO₃^2- can be obtained from the second process in the diagram in 1:2 mole ratio of carbonate ion to hydrogen ion. $? m o l_{C O_{_{3}}^{2 -}} = 1.04 \times 10^{- 3} m o l_{H^{+}} (\frac{1 m o l_{C O_{3}^{2 -}}}{2 m o l_{H^{+}}}) = 0.520 \times 10^{- 3} m o l_{C O_{3}^{2 -}}$ 5) We can also obtain the number of g of CO₃^2- as well, $? g_{C O_{_{3}}^{2 -}} = 1.04 \times 10^{- 3} m o l_{H^{+}} (\frac{1 m o l_{C O_{3}^{2 -}}}{2 m o l_{H^{+}}}) (\frac{60.01 g_{C O_{3}^{2 -}}}{1 m o l_{C O_{3}^{2 -}}}) = 3.12 \times 10^{- 2} g_{C O_{3}^{2 -}}$ 6) This gives us the number of g of M²⁺ ion in the sample, $? g_{M^{2 +}} = 0.1022 g - 3.12 \times 10^{- 2} g_{C O_{3}^{2 -}} = 0.0710 g_{M^{2 +}}$ 7) Then, the molar mass is calculated as $μ_{M^{2 +}} = \frac{0.0710 g}{0.520 \times 10^{- 3} m o l} = 136.538 g / m o l = 137 g / m o l$

Looking up the Periodic Table reveals that the metal ion is Barium, Ba with its molar mass, 137.33 g/mol.

Example:1.128 A 5.012-g sample of an iron chloride hydrate was dried in an oven. The mass of the anhydrous compound was 3.195 g. The compound was then dissolved in water and reacted with an excess of AgNO3. The AgCl precipitate formed weighed 7.225 g. What is the formula of the original compound?

Example:1.131 The concentration of lead ions (Pb²⁺) in a sample of polluted water that also contains nitrate ions (NO₃^-) is determined by adding solid sodium sulfate (Na₂SO₄) to exactly 500 mL of the water. (a) Write the molecular and net ionic equations for the reaction. (b) Calculate the molar concentration of Pb2+ if 0.00450 g of Na₂SO₄ was needed for the complete precipitation of Pb²⁺ ions as PbSO₄.

(a) The polluted sample contains Pb²⁺ and NO₃^-,and by adding Na₂SO₄ precipitates out PbSO₄. Therefore, the molecular equation is:

Pb(NO₃)₂(aq) + Na₂SO₄(aq) → 2NaNO₃(aq) + PbSO₄(s)

There are spectator ions and are: Na⁺ and NO₃^- So they will be canceled out in the net ionic equation:

Pb²⁺(aq) + SO₄^2-(aq) → PbSO₄(s)

(b) The concentration of [Pb²⁺] is given in molarity by: $[P b^{2 +}] = \frac{m o l_{p b^{2 +}}}{L_{P b^{2 +}}}$ for which the denominator is known, 500 mL or 0.5 L. It means that the question is really asking about the number of moles of Pb ion by using 0.00450 g of Na₂SO₄. $? m o l_{P b^{2 +}} = 0.00450 g_{N a_{2} S O_{4}} (\frac{1 m o l_{N a_{2} S O_{4}}}{105.9888 g_{N a_{2} S O_{4}}}) (\frac{1 m o l_{S O_{4}^{2 -}}}{1 m o l_{N a_{2} S O_{4}}}) (\frac{1 m o l_{P b S O_{4}}}{1 m o l_{S O_{4}^{2 -}}}) (\frac{1 m o l_{P b^{2 +}}}{1 m o l_{P b S O_{4}}}) = 4.2457 \times 10^{- 5} m o l_{P b^{2 +}}$

Then, the result is used to convert it into molarity unit,

$[P b^{2 +}] = \frac{4.2457 \times 10^{- 5} m o l_{p b^{2 +}}}{0.5 L_{P b^{2 +}}} = 8.49146 \times 10^{- 5} M = 8.49 \times 10^{- 5} M$

Example:1.145 Acetylsalicylic acid (C₉H₈O₄) is a monoprotic acid commonly known as "aspirin." A typical aspirin tablet, however, contains only a small amount of the acid. In an experiment to determine its composition, an aspirin tablet was crushed and dissolved in water. It took 12.25 mL of 0.1466 M NaOH to neutralize the solution. Calculate the number of grains of aspirin in the tablet. (One grain = 0.0648 g.)

It is presumed that the acetylsalicylic acid (weak acid) reacts with sodium hydroxide, the strong base, thus the net ionic equation is

C₉H₈O₄ + OH^- → H₂O + C₉H₇O₄^- Then, we can calculate the grains of acetylsalicylic acid in straight-forward manner,

$? g r a i n_{s a l} = 12.25 m L_{N a O H} (\frac{0.1466 m o l_{N a O H}}{10^{3} m L_{N a O H}}) (\frac{1 m o l_{O H^{-}}}{1 m o l_{N a O H}}) (\frac{1 m o l_{s a l}}{1 m o l_{O H^{-}}}) (\frac{180.157 g_{s a l}}{1 m o l_{s a l}}) (\frac{1 g r a i n_{s a l}}{0.0648 g_{s a l}}) = 4.99282 g r a i n s = 4.99 g r a i n s$

Example:4.162 A quantity of 25.0 mL of a solution containing both Fe²⁺ and Fe³⁺ ions is titrated with 23.0 mL of 0.0200 M KMnO₄ (in dilute sulfuric acid). As a result, all of the Fe²⁺ ions are oxidized to Fe³⁺ ions. Next, the solution is treated with Zn metal to convert all of the Fe³⁺ ions to Fe²⁺ ions. Finally, the solution containing only the Fe²⁺ ions requires 40.0 mL of the same KMnO₄ solution for oxidation to Fe³⁺. Calculate the molar concentrations of Fe²⁺ and Fe³⁺ in the original solution. The net ionic equation is

MnO₄^- + 5Fe²⁺ → Mn²⁺ + 5Fe³⁺ + 4H₂O

So, we need to know the [Fe²⁺]_original and [Fe³⁺]_original, both of which we do know the volume, 25.0 mL.

The first titration give the Fe²⁺ in the original solution. The second titration gives the total amount of Fe in the solution. By this time, all Fe ions are converted to Fe²⁺. Thus, by calulating the amount of Fe²⁺ in the second titration and its difference with the first one gives the [Fe³⁺]_original.

$? m o l_{F e^{2 +}} = 23.0 m L_{K M n O_{4}} (\frac{0.0200 m o l_{K M n O_{4}}}{1000 m L_{K M n O_{4}}}) (\frac{5 m o l_{F e^{2 +}}}{1 m o l_{K M n O_{4}}}) = 2.30 \times 10^{- 3} m o l_{F e^{2 +}}$

$? m o l_{F e^{2 +}} = 40.0 m L_{K M n O_{4}} (\frac{0.0200 m o l_{K M n O_{4}}}{1000 m L_{K M n O_{4}}}) (\frac{5 m o l_{F e^{2 +}}}{1 m o l_{K M n O_{4}}}) = 4.00 \times 10^{- 3} m o l_{F e^{2 +}}$

$m o l_{F e^{3 +}} = (4.00 - 2.30) \times 10^{- 3} m o l = 1.70 \times 10^{- 3} m o l_{F e^{3 +}}$

$[F e^{2 +}] = \frac{2.30 \times 10^{- 3} m o l_{F e^{2 +}}}{25.0 m L (\frac{1 L}{10^{3} m L})} = 0.0920 M_{F e^{2 +}}$

$[F e^{3 +}] = \frac{1.70 \times 10^{- 3} m o l_{F e^{3 +}}}{25.0 m L (\frac{1 L}{10^{3} m L})} = 0.0680 M_{F e^{3 +}}$

Example: 2.111 A sample of naturally occuring silicon consists of ²⁸Si (27.9869 amu), ²⁹Si (28.9765 amu) and ³⁰Si (29.9738 amu). If the atomic mass of silicon is 28.0855 and the natural abundance of ²⁹Si is 4.68 %, what are the natural abundances of ²⁸Si and ³⁰Si?

This is solved exactly the same way as we did in the class for copper. The key equation is $〈 m 〉 = c_{28} m_{28} + c_{29} m_{29} + c_{30} m_{30}$ for which we know < m >, all masses of isotopes, and c₂₉. So, we have an equation with two unknowns. We need one more relation. We have for natural abundance in fractional form, $c_{28} + c_{29} + c_{30} = 1$ We rearrange above to solve for c₂₈, we get $c_{28} = 1 - c_{29} - c_{30}$ Substitute this into the first equation, we have $〈 m 〉 = (1 - c_{29} - c_{30}) m_{28} + c_{29} m_{29} + c_{30} m_{30}$ Isolate c₃₀, $c_{30} = \frac{〈 m 〉 - c_{29} m_{29} - m_{28} + c_{29} m_{28}}{(m_{30} - m_{28})}$ Put numbers in $c_{30} = \frac{28.0855 a m u - (0.0468 \cdot 28.9765 a m u) - 27.9869 a m u + (0.0468 \cdot 29.9738 a m u)}{29.9738 a m u - 27.9869 a m u}$ which gives c₃₀ = 0.073115728 = 0.0731 or 7.31%. Then, c₂₈ is 100% - 4.68 - 7.31 = 88.0%.

Example: Calcium levels in blood can be determined by adding oxalate ion to precipitate calcium oxalate, CaC₂O₄, followed by dissolving the precipitate in aqueous acid and titrating the resulting oxalic acid, H₂C₂O₄, with KMnO₄:

5H₂C₂O₄ + 2MnO₄^- + 6H⁺ → 10CO₂ + 2Mn²⁺ + 8H₂O How many mg of Ca²⁺ are present in 10.0 mL of blood if 21.08 mL of 0.000 988M KMnO₄ solution is needed for the titration?

Example: Iodine, I₂, reacts with aqueous thiosulfate ion in neutral solution according to the balanced equation

I₂ + 2S₂O₃^2- → S₄O₆^2- + 2I^- How many g of I₂ are present in a solution if 35.20 mL of 0.150 M Na₂S₂O₃ solution is needed to titrate the I₂ solution?

Chapters 3 and 4 Additional & Practice Problems

Chemical Calculation

Chapter 4 Practice Problems